This set of Mechanical Metallurgy Multiple Choice Questions & Answers (MCQs) focuses on “Element of Plasticity Theory – Invariant of Stress & Strain”.
1. For the biaxial plane stress condition, the von Mises yield criteria can be expressed as ___________
Given that principal stresses are σ1, σ2, σ3 where σ2=0 and yield stress is σo.
a) σ1+ σ3 = σo
b) σ12+σ32 – σ1σ3 = σo2
c) σ1+ σ3 – σ1σ3 = σo2
d) σ1+ σ3 – σ1σ3 = σo
View Answer
Explanation: According to the von-mises condition for yielding:
=> σo= 1/√2 [(σ1-σ2)2+(σ2– σ3)2+(σ3– σ1)2]1/2
Substitute the σ2=0. The equation will reduce to σ12+σ32 – σ1σ3 = σo2
2. For the biaxial plane stress condition, the von Mises yield criteria can be expressed as:
σ12+σ32 – σ1σ3= σo2
The above equation physically represents _________
a) circle
b) straight line
c) ellipse
d) parabola
View Answer
Explanation: Considering the σ1, σ3 as the x-axis and y-axis respectively. σo2 is a constant, so the equation is the standard form of an ellipse whose major axis is √2σo and minor axis is √(2/3)σo
3. The following diagram represents the equation σ12+σ32 – σ1σ3 = σo2 for the von-mises condition.
The plot is known as the yield locus for Von-Mises criteria. Which of the following statement is not correct?
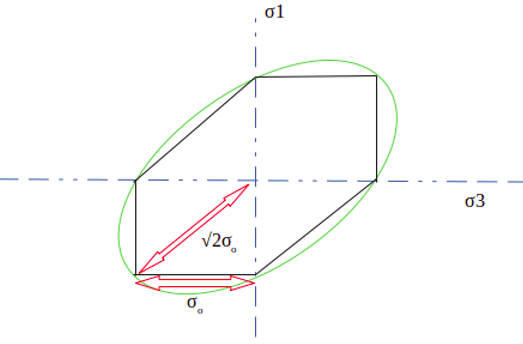
a) The yield locus of Tresca criteria falls inside the of the Von-Mises criteria
b) Both the Von-Mises and Tresca’s method predicts the same yield stress for uniaxial stress
c) Both the Von-Mises and Tresca’s method predicts the same yield stress for balance biaxial stress
d) The yield locus of Tresca criteria falls outside the of the Von-Mises criteria
View Answer
Explanation: Physically, the ellipse can be interpreted as follows: if the stress value is inside the ellipse, the material is safe and will not yield; and if outside the ellipse, it will yield. The green ellipse represents the Von-Mises criteria, and black lines inside the ellipse represents the Tresca’s criteria. On the x-axis, y-axis and balanced 45 degrees, both the criteria predict the same value.
4. The greatest divergence in predicting the yield stress for distortion between the Tresca’s criteria and Von-Mises criteria occurs at __________
a) uniaxial tension/compression
b) balanced biaxial stress
c) pure shear stress
d) always predicts equal stress
View Answer
Explanation: The following diagram represents both the Tresca’s and von-mises criteria for yielding.
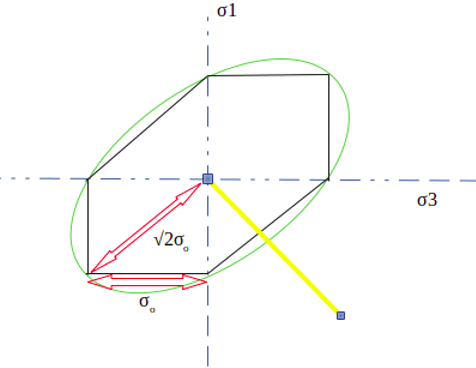
For the uniaxial tension/compression and balanced biaxial stress, the yield stress for both the cases are the same. In the case of pure shear σ1=-σ3 (shown by the yellow line) shows the maximum deviation in predicted yield stress values.
5. Von-mises and Tresca yielding criteria applies to both the isotropic and anisotropic materials.
a) True
b) False
View Answer
Explanation: The empirical model of yielding criteria is valid only for isotropic materials. It fails to predict the correct yielding behavior for anisotropic material such as cold rolled sheet, long drawn tubes, etc.
6. In the following diagram, the green ellipse shows the yielding criteria according to von-mises for isotropic material. What does the red ellipse represent?
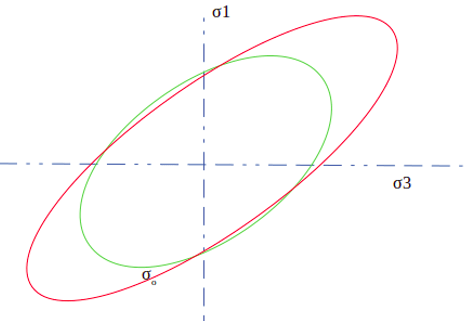
a) Tresca’ yielding criteria for isotropic material
b) Von-mises yielding criteria for anisotropic material
c) Tresca’s yielding criteria for anisotropic material
d) Experimental data of von-mises criteria for isotropic material
View Answer
Explanation: The strength of material along the specific direction is higher than other direction in case of the anisotropic material. So, the predicted yield stress along a certain direction will be higher, and for a particular direction, it will be lower, when compared with isotropic material.
7. Octahedral stresses are the stresses acting on the faces of a three-dimensional octahedron which has the geometric property that the faces of the planes make equal angles with each of the three principal directions of stresses.
a) True
b) False
View Answer
Explanation: Octahedral stresses are the equivalent of mean stress acting on the body. In the geometric body, the angle between the normal to one of the faces and the nearest principal axis is 54°44′, and the cosine of this angle is 1/ V. This is equivalent to {111} plane in an FCC crystal lattice.
8. The levy mises stress-strain relation equation is used for _____________
a) elastic material
b) ideal Plastic material
c) viscous material
d) elastic-plastic material
View Answer
Explanation: The relationship between ideal plastic solid where elastic strain is negligible are called flow curve of the levy mises equations.
The generalized lavy mises equation is:
\(\frac{d\epsilon 1}{\sigma 1′}=\frac{d\epsilon 2}{\sigma 2′}=\frac{d\epsilon 3}{\sigma 3′}=d\lambda ‘\)
9. The Prandtl-Reuss stress strain relation equation is used for _____________
a) elastic material
b) ideal Plastic material
c) viscous material
d) elastic-plastic material
View Answer
Explanation: The Levy-Mises equations can only be applied to problems of large plastic deformation because they neglect elastic strains. To treat the important, but more difficult problems in the elastic-plastic region, it is necessary to consider both elastic and plastic components of strain. These equations were proposed by Prandtl (1925) and Reuss (1930).
Sanfoundry Global Education & Learning Series – Mechanical Metallurgy.
To practice all areas of Mechanical Metallurgy, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Practice Metallurgical Engineering MCQs
- Check Mechanical Metallurgy Books
- Check Metallurgical Engineering Books
- Apply for Metallurgical Engineering Internship
