This set of Mechanical Metallurgy Multiple Choice Questions & Answers (MCQs) focuses on “Low-Curve Fatigue”.
1. The Gerber line is shown by which of the following curve/line?
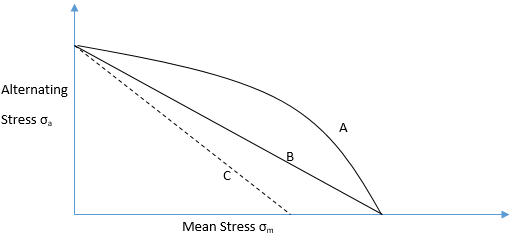
a) A
b) B
c) C
d) Not shown in the figure
View Answer
Explanation: The Gerber parabola connects the endurance limit to the maximum tensile strength of the material. It does not follow the path of a straight line.
2. The point X in the above diagram indicates the ________
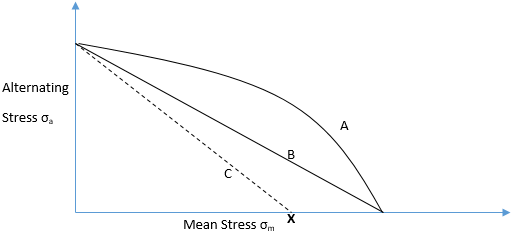
a) tensile point
b) minimum stress point
c) maximum stress point
d) yield point
View Answer
Explanation: The point X is the yield point of the material, and the line connecting the alternating stress to the yield point is called the Soderberg line.
3. In the Haig-Soderberg diagram, the test data for ductile material falls near the ______________
a) Soderberg line
b) Goodman Line
c) Gerber line
d) Haig line
View Answer
Explanation: The test data for ductile material follows the parabolic path, and the Gerber line is the one which follows the parabolic path.
4. The test data for Notched specimen fall near the ________________ line.
a) Soderberg line
b) Goodman Line
c) Gerber line
d) Haig line
View Answer
Explanation: The fatigue test data are scattered too much, so the results generally follow the Goodman line. The straight line connects the alternating stress point to the tensile point.
5. The relationship between the alternating stress and mean stress is given by the following equation:
σa= σe[1-(σm/σu)x].
The value of x for Goodman line is equal to _________
a) 1
b) 2
c) 0.5
d) -1
View Answer
Explanation: The Goodman line follows a straight-line path. So, when the value of x is equal to one, the equation σa= σe[1-(σm/σu)x] becomes the equation of the straight line.
6. The relationship between the alternating stress and mean stress is given by the following equation:
σa=σe[1-(σm/σu)x], where σe is the fatigue limit for completely reversed loading.
The value of x for Gerber line is equal to _________
a) 1
b) 2
c) 0.5
d) -1
View Answer
Explanation: The Gerber line follows the path of a parabola. So, if value of x is kept two, the equation satisfies the equation of the parabola.
7. A steel bar having diameter 14 m is subjected to a fluctuating load of 50 kN in tension and 10 kN in compression. Find the mean stress of the steel bar?
a) 52 Pa
b) 130 Pa
c) 505 Pa
d) 5151 Pa
View Answer
Explanation: The cross sectional area of the rod:
-> π(D/4)2
-> (22/7)*7*7 = 154 m2
Maximum stress = 50000/154 = + 324.67
Minimum stress = 10000/154 = – 64.93
Mean stress = (324.67-64.93)/2 = 129.86 Pa.
8. A steel bar having diameter 14 m is subjected to a fluctuating load of 50 kN in tension and 10 kN in compression. Find the alternating stress of the steel bar?
a) 5482 Pa
b) 130 Pa
c) 194 Pa
d) 515 Pa
View Answer
Explanation: The cross sectional area of the rod:
-> π(D/4)2
-> (22/7)*7*7 = 154 m2
Maximum stress = 50000/154 = + 324.67
Minimum stress = 10000/154 = – 64.93
Mean stress = (324.67-(-64.93))/2 = 194.8 Pa.
9. For a given component, the alternating stress is equal to 250 MPa, Mean stress is 100 MPa, and the ultimate tensile strength is 500 MPa. Find the yield strength of the material according to Goodman’s approach?
a) 3125.5 MPa
b) 312.5 MPa
c) 5215.3 MPa
d) 521.5 MPa
View Answer
Explanation: According to Goodman’s approach the:
σa= σe[1-(σm/σu)x]; where the x=1
So the equation becomes σa= σe[1-(σm/σu)]
Substituting the values in the equation:
-> 250 = σe[1-(100/500)]
-> σe = 250*(5/4)
-> σe = 312.5 MPa.
10. For a given component, the alternating stress is equal to 250 MPa, Mean stress is 100 MPa, and the ultimate tensile strength is 500 MPa. Find the yield strength of the material according to the Gerber’s approach?
a) 521 MPa
b) 694 MPa
c) 45 MPa
d) 55 MPa
View Answer
Explanation: According to the Gerber’s approach the:
σa= σe[1-(σm/σu)x]; where the x=2
So the equation becomes the σa= σe[1- (σm/σu)2]
-> 250 = σe [1-(4/5)2]
-> σe = 694.44 MPa.
Sanfoundry Global Education & Learning Series – Mechanical Metallurgy.
To practice all areas of Mechanical Metallurgy, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Apply for Metallurgical Engineering Internship
- Check Mechanical Metallurgy Books
- Check Metallurgical Engineering Books
- Practice Metallurgical Engineering MCQs
