This set of Basic Mechanical Metallurgy Questions and Answers focuses on “Element of Plasticity Theory – Yielding Criteria for Ductile Metal”.
1. The yielding criteria are primarily empirical relations. Pure hydrostatic stress causes the yielding in continuous solid.
a) True
b) False
View Answer
Explanation: The hydrostatic component of the complex state of stress does not influence the value of stress at which yielding occurs. Stress deviator is involved with yielding.
2. Von-mises or Distortion-energy Criteria proposed that yielding will occur when the second invariant of the stress deviator J2 exceeds some critical value. The second invariant of the stress deviator J2 is equal to __________
a) 1/6 [(σ1 – σ2)2+(σ2 – σ3)2+(σ3 – σ1)2]
b) 1/2 [(σ1 – σ2)2+(σ2 – σ3)2+(σ3 – σ1)2]
c) [σ1 + σ2 + σ3]
d) 1/2 [(σ1 – σ2)+(σ2 – σ3)+(σ3 – σ1)]
View Answer
Explanation: Von-mises proposed the idea that distortion stress of any material should be independent of the principal stress direction. In other word, it must result in an invariant quantity which is equal to 1/6 [(σ1 – σ2)2+(σ2 – σ3)2+(σ3 – σ1)2].
3. According to Von-mises, yielding occurs when J2 exceeds some constant k2
So, the minimum condition for yielding is J2=k2
Find the value of k in uniaxial tension. Given that yield strength = σo
a) σo
b) σo/2
c) σo/3
d) σo/√3
View Answer
Explanation: In the case of uniaxial tension
=> σ1 = σo, σ2=0, σ3=0
So according to the condition J2 = k2
=> J2 = 1/6 [(σ1-σ2)2+(σ2 – σ3)2+(σ3-σ1)2]
=> J2 = 1/6 [(σo – 0)2+(0)2+(0-σo)2]
=> J2 = 1/3[σo2]
J2 = k2
=> 1/3[σo2] = k2
=> k = σo/√3.
4. The final result for von-Mises theory for the distortion relating the yield stress with stress deviator is:
σo = 1/√2 [(σ1-σ2)2+(σ2-σ3)2+(σ3-σ1)2]1/2
Where σo yield stress in uniaxial tension.
a) True
b) False
View Answer
Explanation: According to the theory, yielding will occurs when the second invariant of the stress deviator J2 exceeds some critical value J2=k2
J2=1/6 [(σ1-σ2)2+(σ2– σ3)2+(σ3-σ1)2]
k=σo/√3
So:
1/3[σo2] = 1/6 [(σ1-σ2)2+(σ2-σ3)2+(σ3-σ1)2]
σo = 1/√2 [(σ1-σ2)2+(σ2-σ3)2+(σ3-σ1)2]1/2
So, when R.H.S. value excessed σo yielding will occur in the material.
5. Stress analysis of structural material for the submarine gives the state of stress as shown in the figure. The yield strength of the material is 450 MPa. Using Von-mises yielding criteria determine whether yielding will occur or not? If not, what is the factor of safety?
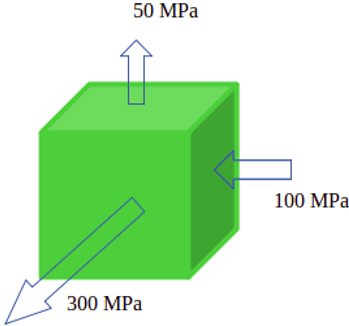
a) Yielding will not occur
b) Yielding will occur, and the factor of safety is 2.5
c) Yielding will occur, and the factor of safety is 1.53
d) Yielding will occur, and the factor of safety is 1.28
View Answer
Explanation: criteria for yielding is R.H.S should be greater than 450MPa
σo = 1/√2 [(σ1-σ2)2+(σ2-σ3)2+(σ3-σ1)2]1/2
σ1=300 MPa, σ2=50 MPa, σ3=-100MPa
R.H.S = 1/√2 [(σ1-σ2)2+(σ2-σ3)2+(σ3-σ1)2]1/2
=> 1/√2 [(300- 50)2+(50-(-100))2+((-100-300)2]1/2
=> 350MPa
yield stress (σo=450MPa) is more than stress deviator so yielding will not occur.
The factor of safety = 450/350 = 1.285.
6. According to Von-mises yielding occur when J2 Exceeded some constant k2
So, the minimum condition for yielding is J2 = k2
Find the value of k in state of pure shear. Given that yield strength in pure torsion = τ.
a) τ
b) τ/3
c) τ/√3
d) τ/2
View Answer
Explanation: In the state of pure shearσ1= -σ3= τ andσ2=0
Condition for yielding 1/6 [(σ1-σ2)2+(σ2-σ3)2+(σ3-σ1)2]=k2
=> 1/6 [(τ – 0)2+(0-(-τ))2+(-τ -τ)2]
=> 1/6(6 τ2) = τ2
So τ2=k2
=> k = τ
So, the constant k is equal to yield strength in pure torsion.
7. Physical Meaning of von-mises yielding criteria is that yielding occurs when the _____________ reaches a critical value.
a) distortion energy
b) strain energy
c) potential energy
d) kinetic energy
View Answer
Explanation: Physical Meaning on von-mises yielding criteria is that yielding occurs when the distortion energy reaches a critical value. The distortion energy is part of strain energy per unit volume that is involved in a change of shape as opposed to a change in volume.
8. Tresca or maximum-shear stress criteria assumes that yielding occurs when the maximum shear stress reaches a value of the shear stress in the uniaxial tension test. Assume the principal stress being σ1, σ2, σ3 where σ1 is largest, and σ3 is the smallest principal stresses. Find the value of minimum shear stress to cause yielding, given that yield stress in tension is equal to σo?
a) τ = σo
b) τ = σo/2
c) τ = σo/3
d) τ = σo/4
View Answer
Explanation: As given in the question, the yielding will occur when maximum shear reaches a value equal to shear stress in tension.
Maximum shear stress = (σ1-σ3)/2
Maximum shear stress in pure tension=σo/2
So, τmax = (σ1-σ3)/2=σo/2
Also (σ1-σ3)=σo
9. The value of constant k in Tresca’s yielding criteria in case of pure shear will be equal to ___________ Given that Principle stress being σ1, σ2, σ3 and yield stress in tension and pure shear are equal to σo and τ.
a) k = σo
b) k = σo/2
c) k = σo/3
d) k = σo/4
View Answer
Explanation: For the state of pure shear σ1= -σ2=τo, and σ3=0.
The maximum shear stress will (σ1– σ2)/2 = τo
This τo should be equal to maximum shear in pure tension.
τo = σo/2=k.
10. Stress analysis of structural material for the submarine gives the state of stress as shown in the figure. The yield strength of the material is 450 MPa. Using Tresca’s yielding criteria determine whether yielding will occur or not? If not, what is the factor of safety?

a) Yielding will not occur
b) Yielding will occur, and the factor of safety is 1.125
c) Yielding will occur, and the factor of safety is 1.53
d) Yielding will occur, and the factor of safety is 1.28
View Answer
Explanation: According to Tresca’s criteria
τmax = (σ1– σ3)/2 should be greater than σo/2 for yielding to occur.
=> τmax = (σ1– σ3)/2
=> τmax = (300-(-100))/2 = 200 MPa
Shear stress in pure tension is σo/2
=> 450/2 = 225 MPa
Factor of safety = 225/200 = 1.125.
Sanfoundry Global Education & Learning Series – Mechanical Metallurgy.
To practice basic questions and answers on all areas of Mechanical Metallurgy, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Check Mechanical Metallurgy Books
- Practice Metallurgical Engineering MCQs
- Check Metallurgical Engineering Books
- Apply for Metallurgical Engineering Internship
