This set of Mechanical Metallurgy Multiple Choice Questions & Answers (MCQs) focuses on “Elastic Behaviour – Strain Energy”.
1. The elastic strain energy is equal to the area under the stress-strain curve up (from origin to the elastic limit).
a) True
b) False
View Answer
Explanation: Elastic strain energy is equal to the area under the load vs elongation curve because the power is equal to force x distance. The area under the stress-strain curve up to the elastic limit is called resilience.
2. Elastic strain energy per unit volume or strain energy density is NOT equal to ________
Where σx=stress in x direction, εx=strain in x direction, E=young’s modulus, P=load, Δ=elongation.
a) \(\frac{1}{2}(\sigma x\epsilon x)\)
b) \(\frac{1}{E}(\sigma x^2)\)
c) \(\frac{1}{2}(E\epsilon x^2)\)
d) \(\frac{1}{2}(p \Delta)\)
View Answer
Explanation: Elastic strain energy per unit volume is obtained by dividing total elastic energy with overall volume. Its unit is N/m2; where N-newton, m-meter. Match the unit of all the expression. Only this expression \(\frac{1}{2}(p \Delta)\) has unit N/m2.
3. In the universal testing machine for tension test, the output raw data are in the form of ________
a) Load vs. Elongation
b) Engineering stress vs. Engineering Strain
c) True Stress vs. True strain
d) Torque vs. Angle
View Answer
Explanation: The force/load and the corresponding change in length of the specimen are the two parameters which can be controlled in UTM. In particular, Stress is tough to control in UTM because the area of the sample continuously decreases with elongation. Torque vs angle data is obtained in the torsion test.
4. Elastic constant is greatly influenced by the interatomic force between atoms. The following diagram represents the relationship between the interatomic distance and atomic potential energy. Equilibrium interatomic distance is denoted by point ____________
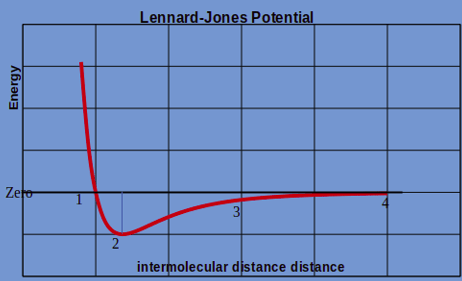
a) 1
b) 2
c) 3
d) 4
View Answer
Explanation: The Equilibrium interatomic distance is the point where the potential energy of the system is minimum. In the diagram it is clearly observed that the point 2 has minimum energy.
5. In the following Potential energy vs. interatomic distance chart, interatomic force between the atoms will be zero at point __________
a) 1
b) 2
c) 3
d) 4
View Answer
Explanation: The interatomic force will be zero at a position where there is no net attraction or repulsion between atoms. In the mathematical term, the is the point where the change in energy with distance is zero. (Slope of the above curve is 0).
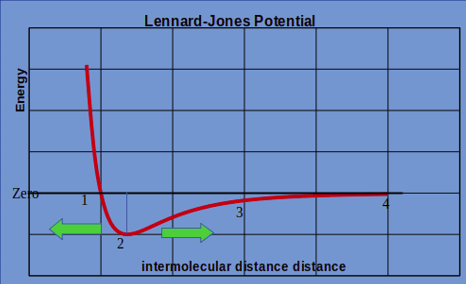
6. If the interatomic distance between 2 atoms is changed from the equilibrium position, then the nature of force will be _____________ when interatomic distance is decreased from equilibrium; and the nature of force will be _____________ when interatomic distance is increased.
a) attractive, repulsive
b) repulsive, attractive
c) attractive, attractive
d) repulsive, repulsive
View Answer
Explanation: Physically, it can be interpreted as when the interatomic distance between 2 atoms reduces, their electron clouds starts overlapping. It causes very high repulsion between two atoms. As the distance increases from equilibrium atomic position, the Van der Waals attraction tries to bring the 2 atoms together and the nature of force will become attractive.
7. Elastic constant of crystal does not vary with the orientation of the crystal.
a) True
b) False
View Answer
Explanation: Elastic constant of crystal does vary with the orientation of the crystal because interatomic distance varies with direction inside a crystal. Elastic constant has a direct relation with the atomic force, which depends upon the interatomic distance.
8. The following equation gives the variation of interatomic energy with atomic distance:
V(r)=4ε[(σ/r12)−(σ/r6)]
Where V(r) is the potential energy and r is interatomic distance. ε and σ are constant.
Find the value of interatomic distance where energy is minimum?
a) 0
b) ε
c) σ
d) 1.2 σ
View Answer
Explanation: For minimum energy
=> d(V(r))/d(r)=0
=> d[4ε[(σ/r12)−(σ/r6)]]/dr=0
=> 4 ε[(-12σ12 r-13)−(-6σ6 r-7)]=0
=> 2 σ6=r6
=> r = 2(1/6) σ
=> r = 1.2 σ.
9. The variation of interatomic energy with atomic distance is given by the following equation V(r)=4ε[(σ/r12)−(σ/r6)]
Where V(r) is the potential energy, and r is interatomic distance. ε and σ are constant.
Find the value of energy at the point where the interatomic force is zero?
a) – ε
b) ε
c) 0
d) σ
View Answer
Explanation: or minimum energy
=> d(V(r))/d(r)=0
=> d[4ε[(σ/r12)−(σ/r6)]]/dr=0
=> 4 ε[(-12σ12 r-13)−(-6σ6 r-7)=0
=> 2 σ6=r6
=> r = 2(1/6) σ
Substitute the value of r in terms of σ in the equation:
=> V(r)=4ε[(σ12/2(1/6) σ12)−(σ6/2(1/6) σ6)] => 4ε(1/4-1/2)
=> -ε.
10. The elastic constant of a material is determined by the ________________ of potential energy vs interatomic distance curve.
a) slope
b) curvature
c) x-intercept
d) minimum
View Answer
Explanation: In an elastic solid bond energy is a continuous function of the displacement (from the mean position of interatomic distance) thus:
Φ(u) = Φo+(∂Φ/∂u)o u+1/2((∂Φ/∂u)o2 u2+ ………….
Where Φ(u) is total potential energy, u is the displacement and Φo is equilibrium potential energy when u=0.
So, the first differentiation of energy will give force at equilibrium (∂Φ/∂u)o=0.
Hence the final expression will be
=> P= (∂Φ/∂u)o2 u, where P= ∂Φ(u)/∂u
This is equivalent to the raw form of Hooke’s law, and the elastic constant will be equal to (∂Φ/∂u)o2, i.e. curvature of the curve.
11. Which of the following factors change the value of the elastic constant of any material?
a) Heat treatment
b) Vacancy
c) Temperature
d) Dislocation
View Answer
Explanation: Elastic constant is only dependent on cohesive energy between atoms in the material. It is not affected by heat treatment and structural defects. The internal cohesive energy of bonding between atoms cannot be changed. Only with an increase in temperature, we can observe a slight decrease in bonding between atoms, so there is a reduction in elastic constant value.
Sanfoundry Global Education & Learning Series – Mechanical Metallurgy.
To practice all areas of Mechanical Metallurgy, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Check Metallurgical Engineering Books
- Check Mechanical Metallurgy Books
- Apply for Metallurgical Engineering Internship
- Practice Metallurgical Engineering MCQs
