This set of Structural Analysis Multiple Choice Questions & Answers (MCQs) focuses on “Influence Line Diagram – Numericals”.
1. Concept of ILD is only applicable to the static indeterminate structure.
a) True
b) False
View Answer
Explanation: Concept of ILD for calculating shear force and bending moment is applicable to both statically determinate and indeterminate structures.
2. ILD for bending moment diagram of the cantilever beam is _______

a) 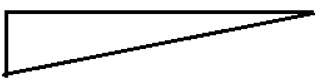
b) 
c) 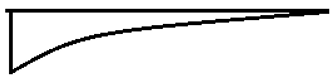
d) 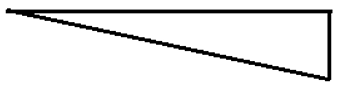
View Answer
Explanation: Maximum bending moment for cantilever beam occurs when the load is placed at free end, therefore ordinate of ILD of bending moment diagram will be maximum at a free end. When the load is at support itself, then the bending moment produced is zero, hence ordinate of ILD is zero.
3. ILD for the shear force at the support of the cantilever beam is __________

a) 
b) 
c) 
d) 
View Answer
Explanation: For drawing ILD of shear force at the support we must neglect the support at the given point and then lift the member providing it unit displacement upward and let the rest of the beam follow the suit.
4. ILD for the shear force at section C for the given simply supported beam is _________
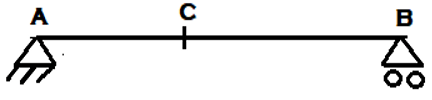
a) 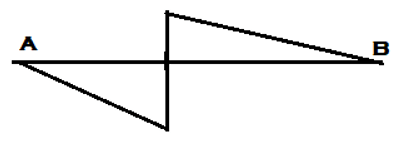
b) 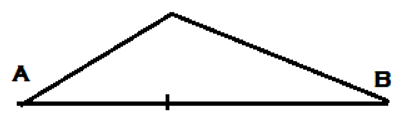
c) 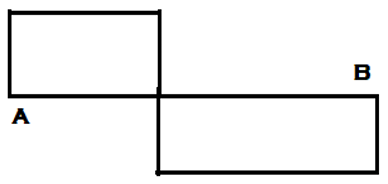
d) 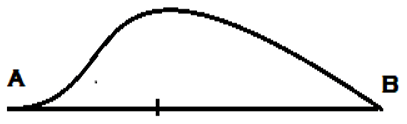
View Answer
Explanation: For drawing ILD of shear force at section, any section other than the support, Assume roller at that section and apply downward push on the left arm of the section and upward push to the right section of the arm. Hence assuming roller at C, Downward and Upward push to the left and right of section respectively.
5. ILD for the bending moment at section C for the given simply supported beam is ________
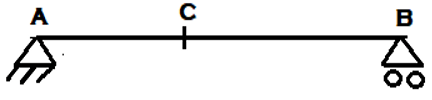
a) 
b) 
c) 
d) 
View Answer
Explanation: To draw ILD for Bending Moment at section E, we must assume internal hinge at the section and apply anticlockwise rotation to the left arm and clockwise rotation to the right of the arm. Thus, assuming an internal hinge at section C and applying rotation to the arms gives us figure B as ILD to bending moment at section C.
6. ILD for Shear force at section E is __________
a) 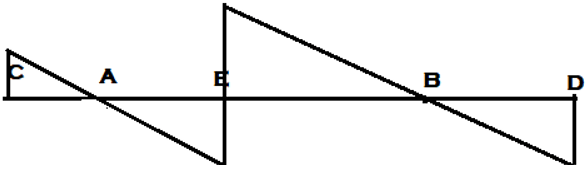
b) 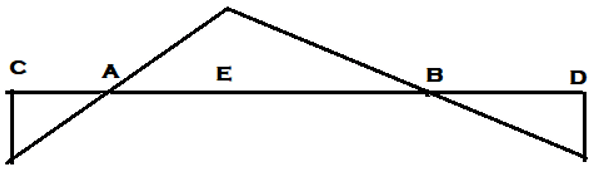
c) 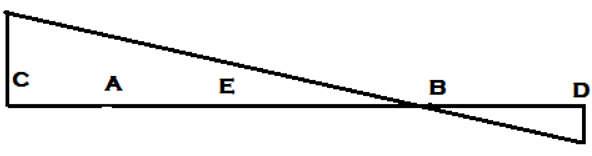
d) 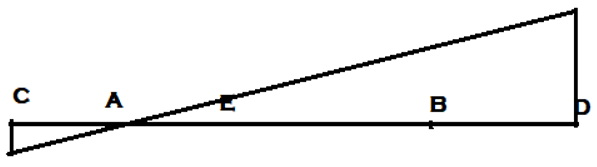
View Answer
Explanation: For drawing ILD of shear force at section, any section other than the support, Assume roller at that section and apply downward push on the left arm of the section and upward push to the right section of the arm. Hence assuming roller at E, Downward and Upward push to the left and right of section respectively.
7. ILD for Shear force at support A is _______
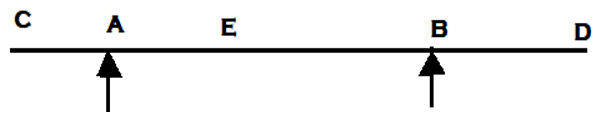
a)

b)

c)

d)

View Answer
Explanation: For drawing ILD of shear force at the support we must neglect the support at the given point and then lift the member providing it unit displacement upward and let the rest of the beam follow the suit.
8. ILD for Shear force at support B is _______
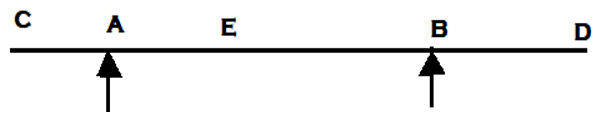
a)

b)

c)

d)

View Answer
Explanation: For drawing ILD of shear force at the support we must neglect the support at the given point and then lift the member providing it unit displacement upward and let the rest of the beam follow the suit.
9. ILD for Shear force at the section just right to the point A is _______
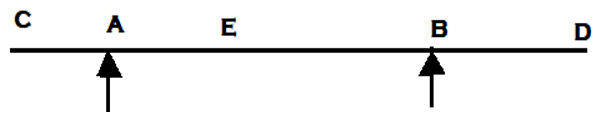
a) 
b) 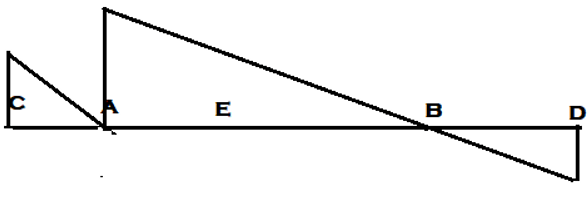
c) 
d) 
View Answer
Explanation: For drawing ILD of shear force at section, any section other than the support, Assume roller at that section and apply downward push on the left arm of the section and upward push to the right section of the arm. But since the ILD is to be drawn for just to the right to A, we have to divide the section to the just right of A.
10. ILD for Bending Moment at section E is ________
a) 
b) 
c) 
d) 
View Answer
Explanation: To draw ILD for Bending Moment at section E, we must assume internal hinge at the section and apply anticlockwise rotation to the left arm and clockwise rotation to the right of the arm. Thus, assuming an internal hinge at section E and applying rotation to the arms gives us figure B as ILD to bending moment at section E.
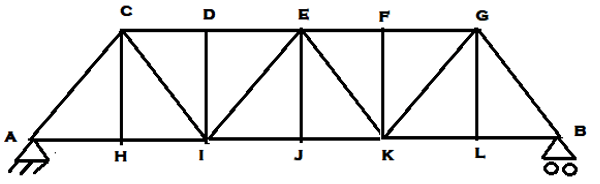
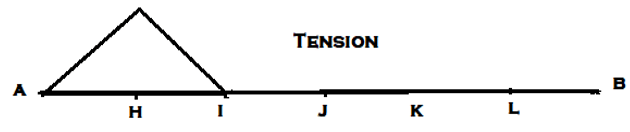
11. ILD for the member DI for the given truss if the unit load rolls along beam AB is ________
a)

b)
c)

d)
View Answer
Explanation: Member DI is a zero force member if the load is supposed to be rolled along bottom beam AB. Therefore, ILD for member DI is zero throughout.
12. ILD for the member CH for the given truss if the unit load rolls along AB is _________

a)

b)

c)

d)

View Answer
Explanation: If unit load is to roll along bottom beam AB, Force produces in CH will be zero if it is at supports or anywhere between joint I to B. However force in member CH will be maximum when load is placed at joint H. Since the truss as a whole structure will sag under the action of load, the member CH will be in tension.
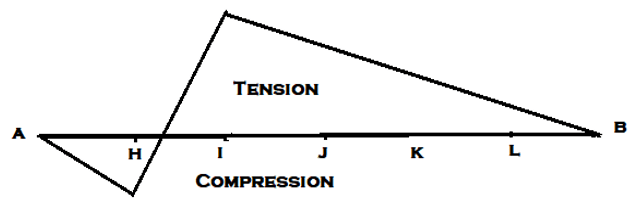
13. ILD for the member CI for the given truss if the unit load rolls along AB is ________

a)

b)

c)

d)

View Answer
Explanation: If a unit load is to roll along bottom beam AB, Force produces in CI will be zero if it is at supports. However, the force in the inclined member CI will change its nature as the load passes through joint H to Joint I. Since the truss as a whole structure will sag under the action of load, the joint C will be under compression and I will be in tension.
14. To draw qualitative ILD of indeterminate structure, which of the following concept is used.
a) Unit Load Method
b) Castigilano’s First energy theorem
c) Mullers Breslou’s Principle
d) Kani’s Method
View Answer
Explanation: Mullers Breslou’s Principle is very useful in performing a qualitative analysis of ILD for indeterminate structure. Unit Load Method, Castigliano’s First Theorem and Kani’s Method are among various methods to determine displacement and rotation in a structure.
15. ILD for a fixed beam is determined by Mullers Brelou’s Principle.
a) True
b) False
View Answer
Explanation: Mullers Breslou’s Principle is very useful in performing a qualitative analysis of ILD for indeterminate structure. The fixed beam is an indeterminate structure and thus, ILD for a fixed beam is determined by Mullers Brelou’s Principle.
Sanfoundry Global Education & Learning Series – Structural Analysis.
To practice all areas of Structural Analysis, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Check Structural Analysis Books
- Check Civil Engineering Books
- Practice Civil Engineering MCQs
- Apply for Civil Engineering Internship
