This set of Structural Analysis Multiple Choice Questions & Answers (MCQs) focuses on “Sections Method Numericals”.
1. Method of the section for determinate truss analysis is time effective.
a) True
b) False
View Answer
Explanation: Method of the section does not require the calculation of forces in the member prior to it. To compute force in any member, we cut the section and establish equilibrium conditions and hence it is time effective method.
2. To find the forces in the vertical member, preferable equilibrium equations are __________
a) ∑H = 0 & ∑M =0
b) ∑H = 0 & ∑V = 0
c) ∑H = 0, ∑V = 0 & ∑M = 0
d) ∑V = 0 & ∑M = 0
View Answer
Explanation: Vertical unknowns at a particular selection should be preferably solved for ∑V = 0 first and later for ∑M = 0. Vertical Member does not have possesses any horizontal component of the forces hence ∑H = 0 is irrelevant to the context.
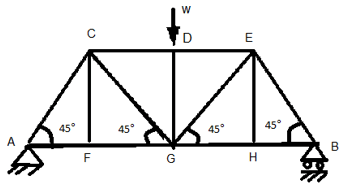
3. What is the force in member CG?
a) 0
b) W
c) W/2
d) W/√2
View Answer
Explanation: ∑V = 0 & ∑M = 0
W/2 = FCG SIN 45°
FCG = W/√2.
4. What is the force in member CD?

a) 0
b) W (Compressive)
c) W (Tensile)
d) W/2 (Compressive)
View Answer
Explanation: ∑MG = 0
FCD X L + (W/2) X 2L = 0

FCD = W (Compressive).
5. What is the force in member FG?

a) 0
b) W/2 (Tension)
c) W/2 (Compression)
d) W (Compressive)
View Answer
Explanation: ∑MC = 0
FFG X L + (W/2) X L = 0
FFG = W/2.

6. What is the force in member EH?

a) 0
b) W ( Compressive)
c) W ( Tension )
d) W/2 (Compressive)
View Answer
Explanation: ∑MB = 0
FHE X L = 0
FHE = 0.
7. Find the Force in member DG.

a) W (Tensile)
b) W (Compressive)
c) 0
d) W/2 (Compressive)
View Answer
Explanation: ∑V = 0
W + FDG = 0
FDG = W (Compressive).
8. Method of the section can always be used to calculate the force in any members.
a) True
b) False
View Answer
Explanation: Method of the section has its own limitation. It cannot be used to compute the force of the member attached to a joint where already forces in more than one member is unknown.
9. Methods of Section can be used to evaluate which of the following truss?
a) 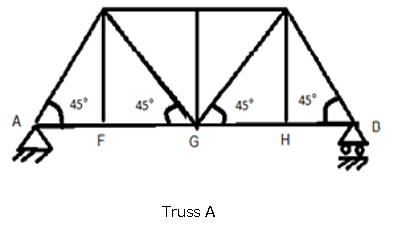
b) 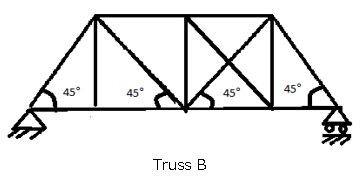
c) 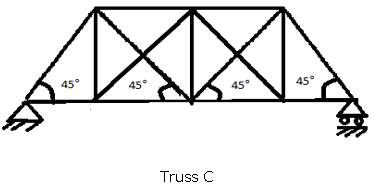
d) 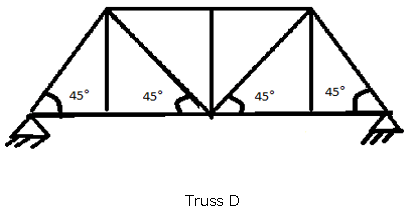
View Answer
Explanation: Truss A is externally and internally determinate and thus it can be evaluated by Method of Section. But Truss B and C are internally indeterminate, Truss D is externally indeterminate and Hence truss B, C, and D cannot be evaluated by Method of Section.
Sanfoundry Global Education & Learning Series – Structural Analysis.
To practice all areas of Structural Analysis, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Check Structural Analysis Books
- Apply for Civil Engineering Internship
- Check Civil Engineering Books
- Practice Civil Engineering MCQs
