Structural Analysis Questions and Answers – Moment Distribution for Beams

This set of Structural Analysis Multiple Choice Questions & Answers (MCQs) focuses on “Moment Distribution for Beams”.

1. Moment Distribution Method is applicable to the determinate and indeterminate structure.
a) True
b) False
View Answer

2. Carryover Moment is defined as ______
a) The moment applied at one end to cause unit slope at the support
b) The additional moment applied at one end to completely resist the rotation caused due to external loading
c) The moment developed or induced at one end due to a moment at another end
d) The moment applied at one end to cause unit slope at another end
View Answer

3. Carryover Moment at end B due to moment M applied at end A for the given propped cantilever beam is _____

a) +M
b) -M
c) +\(\frac{M}{2} \)
d) –\(\frac{M}{2} \)
View Answer

Answer: c
Explanation:

For a moment applied M at the hinged end with a fixed support at another end, the moment applied at the hinged end is halved while getting transferred to the fixed support and hence moment developed is of the half of the magnitude but same direction. The same direction of the moment is indicated by the positive sign and the opposite sign is denoted by a negative sign. Thus, the answer is +\(\frac{M}{2} \).

4. Carryover Moment at end B due to moment M applied at end A for the given beam is _______

a) 0
b) +M
c) -M
d) +\(\frac{M}{2} \)
View Answer

5. Carryover Moment at end B due to moment M applied at end A for the given cantilever beam is ________

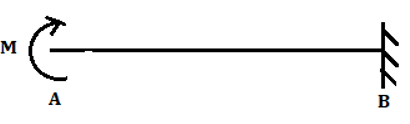
a) +M
b) -M
c) +\(\frac{M}{2} \)
d) –\(\frac{M}{2} \)
View Answer

Answer: b
Explanation:

The moment applied at the free end is completely transferred to the fixed end as a free end cannot resist any moment. Fixed support will develop a resistive moment against the applied moment and hence would be of opposite direction. Therefore, the magnitude of the carryover moment is same and acts in the opposite direction denoted by negative direction.

6. Carryover Moment at end B due to moment M applied at end A for the given beam is ________

a) +M
b) -M
c) +\(\frac{M}{2} \)
d) –\(\frac{M}{2} \)
View Answer

Answer: b
Explanation:

The moment applied at the free end is completely transferred to the roller end as a free end cannot resist any moment. Roller support will develop a resistive moment against the applied moment and hence would be of opposite direction. Therefore, the magnitude of the carryover moment is same and acts in the opposite direction denoted by negative direction.

7. Carryover Moment at end B due to moment M applied at end A for the given non-prismatic beam is ________

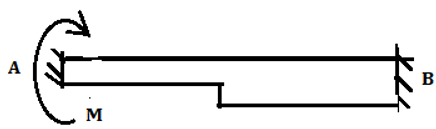
a) 0
b) M
c) Greater than M/2
d) Lesser than M/2
View Answer

8. Moment Distribution Method does not consider axial and shear effects for the displacement calculations for the given structure.
a) True
b) False
View Answer

Sanfoundry Global Education & Learning Series – Structural Analysis.

To practice Structural Analysis Question Bank, here is complete set of 1000+ Multiple Choice Questions and Answers.

If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]