This set of Structural Analysis Multiple Choice Questions & Answers (MCQs) focuses on “Moment Distribution for Frames”.
1. Calculate distribution factor member OA for the shown figure.
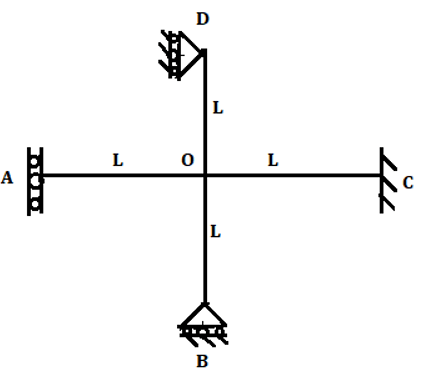
a) \(\frac{1}{8} \)
b) 0
c) \(\frac{3}{8} \)
d) \(\frac{1}{11} \)
View Answer
Explanation: Joint O is connected to the four-member OA, OB, OC, and OD where far end is supported by vertical guided roller, vertical roller support, fixed support, and horizontal roller support respectively.
Stiffness for OA is \(\frac{EI}{L} \)
Stiffness for OB is 0
Stiffness for OC is \(\frac{4EI}{L} \)
Stiffness for OD is \(\frac{3EI}{L} \)
Therefore stiffness for joint O is the sum of the stiffness for all the members connected to it.
Stiffness for the joint O is \(\frac{EI}{L}+0+\frac{4EI}{L}+\frac{3EI}{L}=\frac{8EI}{L} \)
Distribution factor for member OA=\(\frac{Stiffness \, of \, member \, OA}{Stiffness \, of \, rigid \, joint}=\frac{\frac{EI}{L}}{\frac{8EI}{L}}=\frac{1}{8} \)
2. Calculate distribution factor member OC for the shown figure.
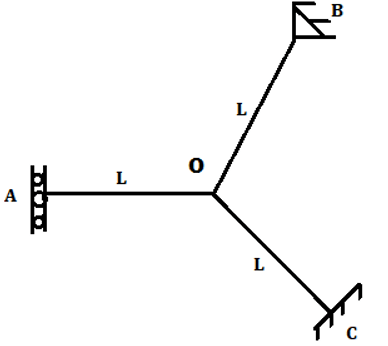
a) \(\frac{2}{3} \)
b) \(\frac{1}{2} \)
c) \(\frac{3}{8} \)
d) \(\frac{1}{8} \)
View Answer
Explanation: Joint O is connected to the four-member OA, OB, and OD where far end is supported by vertical guided roller, fixed support, and hinged support respectively.
Stiffness for OA is \(\frac{EI}{L} \)
Stiffness for OB is \(\frac{3EI}{L} \)
Stiffness for OC is \(\frac{4EI}{L} \)
Therefore stiffness for joint O is the sum of the stiffness for all the members connected to it.
Stiffness for the joint O is \(\frac{EI}{L}+\frac{4EI}{L}+\frac{3EI}{L}=\frac{8EI}{L} \)
Distribution factor for member OC=\(\frac{Stiffness \, of \, member \, OC}{Stiffness \, of \, rigid \, joint}=\frac{\frac{4EI}{L}}{\frac{8EI}{L}}=\frac{1}{2} \)
3. Calculate distribution factor member OB for the shown figure.
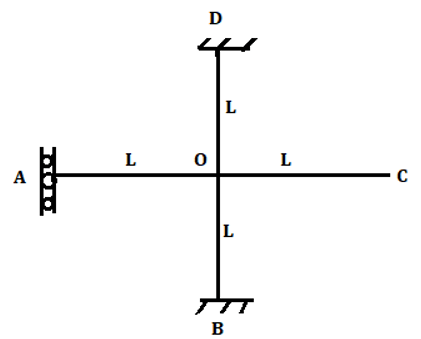
a) \(\frac{3}{4} \)
b) 0
c) \(\frac{4}{9} \)
d) \(\frac{1}{9} \)
View Answer
Explanation: Joint O is connected to the four-member OA, OB, OC, and OD where far end is supported by vertical guided roller, fixed support, the free end, and fixed support respectively.
Stiffness for OA is \(\frac{EI}{L} \)
Stiffness for OB is \(\frac{4EI}{L} \)
Stiffness for OC is 0
Stiffness for OD is \(\frac{4EI}{L} \)
Therefore stiffness for joint O is the sum of the stiffness for all the members connected to it.
Stiffness for the joint O is \(\frac{EI}{L}+0+\frac{4EI}{L}+\frac{4EI}{L}=\frac{9EI}{L} \)
Distribution factor for member OB=\(\frac{Stiffness \, of \, member \, OB}{Stiffness \, of \, rigid \, joint}=\frac{\frac{4EI}{L}}{\frac{9EI}{L}}=\frac{4}{9} \)
4. Calculate distribution factor member BC for the shown figure.
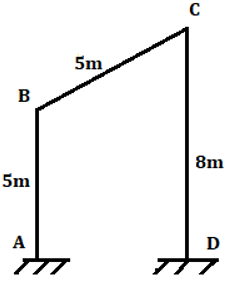
a) \(\frac{4}{13} \)
b) \(\frac{3}{8} \)
c) \(\frac{2}{5} \)
d) \(\frac{1}{2} \)
View Answer
Explanation: Joint B is connected to the members AB and BC where far end for the member AB is fixed supported and far end for the member BC is treated as fixed support.
Stiffness for BA is \(\frac{4EI}{5L} \)
Stiffness for BC is \(\frac{4EI}{5L} \)
Therefore stiffness for joint B is the sum of the stiffness for all the members connected to it.
Stiffness for the joint O is \(\frac{4EI}{5L}+\frac{4EI}{5L}=\frac{8EI}{5L} \)
Distribution factor for member BC=\(\frac{Stiffness \, of \, member \, BC}{Stiffness \, of \, rigid \, joint}=\frac{\frac{4EI}{5L}}{\frac{8EI}{5L}}=\frac{1}{2} \)
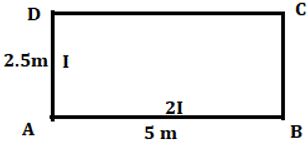
5. Calculate distribution factor member AD for the shown figure.
a) \(\frac{1}{4} \)
b) \(\frac{1}{2} \)
c) \(\frac{3}{4} \)
d) 0
View Answer
Explanation: Joint A is connected to the member’s AD and AB where far end for the member AD and for the member AB both are treated as fixed support.
Stiffness for AB is \(\frac{E*2I}{5L} \)
Stiffness for BC is \(\frac{EI}{2.5L} \)
Therefore stiffness for joint B is the sum of the stiffness for all the members connected to it.
Stiffness for the joint O is \(\frac{E*2I}{5L}+\frac{EI}{2.5L}=\frac{4EI}{5L} \)
Distribution factor for member AD=\(\frac{Stiffness of member BC}{Stiffness \, of \, rigid \, joint}=\frac{2EI}{5L}\frac{4EI}{5L}=\frac{1}{2} \)
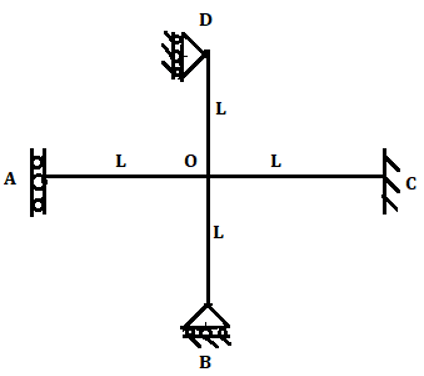
6. Calculate distribution factor member OB for the shown figure.
a) \(\frac{1}{8} \)
b) 0
c) \(\frac{3}{8} \)
d) \(\frac{1}{11} \)
View Answer
Explanation: Joint O is connected to the four-member OA, OB, OC, and OD where far end is supported by vertical guided roller, vertical roller support, fixed support, and horizontal roller support respectively.
Stiffness for OA is \(\frac{EI}{L} \)
Stiffness for OB is 0
Stiffness for OC is \(\frac{4EI}{L} \)
Stiffness for OD is \(\frac{3EI}{L} \)
Therefore stiffness for joint O is the sum of the stiffness for all the members connected to it.
Stiffness for the joint O is \(\frac{EI}{L}+0+\frac{4EI}{L}+\frac{3EI}{L}=\frac{8EI}{L} \)
Distribution factor for member OA=\(\frac{Stiffness \, of \, member \, OA}{Stiffness \, of \, rigid \, joint}=\frac{0}{\frac{8EI}{L}}\)=0
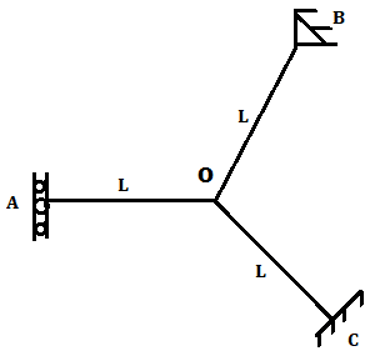
7. Calculate distribution factor member OB for the shown figure.
a) \(\frac{2}{3} \)
b) \(\frac{1}{2} \)
c) \(\frac{3}{8} \)
d) \(\frac{1}{8} \)
View Answer
Explanation: Joint O is connected to the four-member OA, OB, and OD where far end is supported by vertical guided roller, fixed support, and hinged support respectively.
Stiffness for OA is \(\frac{EI}{L} \)
Stiffness for OB is \(\frac{3EI}{L} \)
Stiffness for OC is \(\frac{4EI}{L} \)
Therefore stiffness for joint O is the sum of the stiffness for all the members connected to it.
Stiffness for the joint O is \(\frac{EI}{L}+\frac{4EI}{L}+\frac{3EI}{L}=\frac{8EI}{L} \)
Distribution factor for member OC=\(\frac{Stiffness \, of \, member \,}{Stiffness \, of \, rigid \, joint}=\frac{\frac{3EI}{L}}{\frac{8EI}{L}}=\frac{3}{8} \)
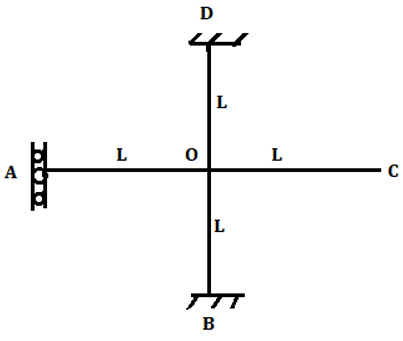
8. Calculate distribution factor member OC for the shown figure.
a) \(\frac{3}{4} \)
b) 0
c) \(\frac{4}{9} \)
d) \(\frac{1}{9} \)
View Answer
Explanation: Joint O is connected to the four-member OA, OB, OC, and OD where far end is supported by vertical guided roller, fixed support, the free end, and fixed support respectively.
Stiffness for OA is \(\frac{EI}{L} \)
Stiffness for OB is \(\frac{4EI}{L} \)
Stiffness for OC is 0
Stiffness for OD is \(\frac{4EI}{L} \)
Therefore stiffness for joint O is the sum of the stiffness for all the members connected to it.
Stiffness for the joint O is \(\frac{EI}{L}+0+\frac{4EI}{L}+\frac{4EI}{L}=\frac{9EI}{L} \)
Distribution factor for member OC=\(\frac{Stiffness \, of \, member \, OC}{Stiffness \, of \, rigid \, joint}=\frac{0}{\frac{9EI}{L}} \)
=0
9. Calculate distribution factor member BA for the shown figure.

a) \(\frac{3}{4} \)
b) \(\frac{1}{4} \)
c) \(\frac{3}{7} \)
d) \(\frac{4}{7} \)
View Answer
Explanation: Joint B is connected to the members BA and BC where far end is supported by fixed support and roller support respectively.
Stiffness for BA is \(\frac{4EI}{L} \)
Stiffness for BC is \(\frac{3EI}{L} \)
Therefore stiffness for joint B is the sum of the stiffness for all the members connected to it.
Stiffness for joint B is \(\frac{4EI}{L}+\frac{4EI}{L}=\frac{7EI}{L} \)
Distribution factor for member BA=\(\frac{Stiffness \, of \, member \, BA}{Stiffness \, of \, rigid \, joint}=\frac{\frac{4EI}{L}}{\frac{7EI}{L}}=\frac{4}{7} \)
10. Calculate distribution factor member BA for the shown figure.
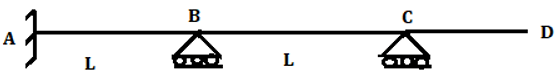
a) \(\frac{3}{4} \)
b) \(\frac{1}{4} \)
c) \(\frac{3}{7} \)
d) \(\frac{4}{7} \)
View Answer
Explanation: Joint B is connected to the members BA and BC where far end is supported by fixed support and roller support respectively.
Stiffness for BA is \(\frac{4EI}{L} \)
Stiffness for BC is \(\frac{3EI}{L} \)
Therefore stiffness for joint B is the sum of the stiffness for all the members connected to it.
Stiffness for joint B is \(\frac{4EI}{L}+\frac{4EI}{L}=\frac{7EI}{L} \)
Distribution factor for member BA=\(\frac{Stiffness \, of \, member \, BA}{Stiffness \, of \, rigid \, joint}=\frac{\frac{4EI}{L}}{\frac{7EI}{L}}=\frac{4}{7} \)
Sanfoundry Global Education & Learning Series – Structural Analysis.
To practice all areas of Structural Analysis, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Check Structural Analysis Books
- Check Civil Engineering Books
- Apply for Civil Engineering Internship
- Practice Civil Engineering MCQs
