Different forms of an Equation of a Line - Class 11 Maths MCQ

This set of Class 11 Maths Chapter 10 Multiple Choice Questions & Answers (MCQs) focuses on “Various Forms of the Equation of a Line”.

1. If slope of a line is positive then its inclination is ___________
a) right angle
b) acute angle
c) obtuse angle
d) zero
View Answer

Answer: b
Explanation: If inclination is α slope is given by tan α. Given that slope of line is positive which means tan α is positive. We know, tan α is positive in 1^st quadrant i.e. α should be acute angle.

2. If slope of a line is negative then its inclination is ___________
a) right angle
b) acute angle
c) obtuse angle
d) zero
View Answer

Answer: c
Explanation: If inclination is α slope is given by tan α. Given that slope of line is negative which means tan α is negative. We know, tan α is negative in 2^nd quadrant i.e. α should be obtuse angle.

3. Find slope of line joining (1, 2) and (4, 11).
a) 1/3
b) 3
c) 9
d) 1/9
View Answer

Answer: b
Explanation: We know, slope of line joining two points (x₁, y₁) and (x₂, y₂) is given by \(\frac{y_2-y_1}{x_2-x_1}\).
So, slope of line joining (1, 2) and (4, 11) is \(\frac{11-2}{4-1} = \frac{9}{3}\) = 3.

4. If two lines are parallel their inclination angle may be different.
a) True
b) False
View Answer

Answer: b
Explanation: If two lines are parallel then they form same angle with positive direction of x-axis in anticlockwise direction i.e. their inclinations are equal.

5. If two lines are parallel then their slopes must be equal.
a) True
b) False
View Answer

Answer: a
Explanation: Let the inclination of the two lines be α and β. Since they are parallel so, α = β.
=>tan α = tan β. Hence their slopes are equal.

Sanfoundry Certification Contest of the Month is Live. 100+ Subjects. Participate Now!

6. If the two lines are perpendicular then difference of their inclination angle is ________
a) 45°
b) 60°
c) 90°
d) 180°
View Answer

Answer: c
Explanation: If the two lines are perpendicular then if one line form angle α with positive x-axis then the other line form angle 90°+ α.

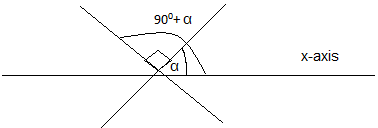
mathematics-questions-answers-various-forms-equation-line-q6

7. If the two lines with slope m₁ and m₂ are perpendicular then their slopes has relation ______
a) m₁ + m₂ = 1
b) m₁ * m₂ = 1
c) m₁ * m₂ = -1
d) m₁ + m₂ = -1
View Answer

Answer: c
Explanation: If the two lines are perpendicular then if one line form angle α with positive x-axis then the other line form angle 90° + α.
If m₁ = tan α then m₂ will be tan (90°+ α) = – cot α = -1/tan α
=> m₁ * m₂ = – 1.

8. If angle between the two lines is 45° and slope of one line is 1/4 then which of the following is possible value of the slope of other line.
a) 5/3
b) 3/5
c) -5/3
d) 4/5
View Answer

Answer: a
Explanation: If angle between two lines with slopes m₁ and m₂ is α then tan α = |(m₁-m₂)/(1+m₁*m₂)|
tan 450 = \(|\frac{m-1/4}{1+m/4}| = \frac{4m-1}{m+4}\)
=>1 = \(\frac{4m-1}{m+4}\) => m+4 = 4m-1 => 3m = 5
=>m = 5/3.

9. If angle between the two lines is 45° and slope of one line is 1/4 then which of the following is possible value of the slope of other line.
a) 3/5
b) -3/5
c) -5/3
d) 4/5
View Answer

Answer: b
Explanation: If angle between two lines with slopes m₁ and m₂ is α then tan α = |(m₁-m₂)/(1+m₁*m₂)|
tan 45° = \(|\frac{m-1/4}{1+m/4}|\)
=> \(\frac{4m-1}{m+4}\) = -1
=>- m-4 = 4m-1 => 5m = -3
=> m = -3/5.

10. If slope of a line is 2/3 then find the slope of line perpendicular to it.
a) -3/2
b) 3/2
c) 2/3
d) -2/3
View Answer

Answer: a
Explanation: If lines with slopes m₁ and m₂ are perpendicular then m₁ * m₂ = – 1.
If m₁ = 2/3 then m₂ = -1 / (2/3) = -3/2.

11. If slope of one line is 1/4 and other is 5/3 then find the angle between two lines.
a) 30°
b) 45°
c) 90°
d) 180°
View Answer

Answer: b
Explanation: If angle between two lines with slopes m₁ and m₂ is α then tan α = |(m₁-m₂)/(1+m₁*m₂)|
tan α = \(|\frac{5/3-1/4}{1+5/3*1/4}| = |\frac{20-3}{12+5}|\) = 17/17 =1 => α = 45°

12. Find slope of line passing through origin and (3, 6).
a) 2
b) 3
c) 1/3
d) 1/2
View Answer

Answer: a
Explanation: We know, slope of line joining two points (x₁, y₁) and (x₂, y₂) is given by (y₂-y₁)/(x₂-x₁).
So, slope of line joining (0, 0) and (3, 6) is (6-0)/(3-0) = 6/3 = 2.

13. If line joining (1, 2) and (5, 7) is parallel to line joining (3, 4) and (11, x).
a) 10
b) 11
c) 12
d) 14
View Answer

Answer: d
Explanation: We know, slope of line joining two points (x₁, y₁) and (x₂, y₂) is given by(y₂-y₁)/(x₂-x₁).
Lines are parallel means slope is equal.
=>(x-4)/(11-3) = (7-2)/(5-1) => x-4 = 5*8/4 = 10 => x=14.

14. If line joining (1, 2) and (7, 6) is perpendicular to line joining (3, 4) and (11, x).
a) 12
b) 16
c) -16
d) -12
View Answer

Answer: c
Explanation: We know, slope of line joining two points (x₁, y₁) and (x₂, y₂) is given by(y₂-y₁)/(x₂-x₁).
Lines are perpendicular means m₁*m₂ = -1
=> \((\frac{x-4}{11-3})(\frac{6-2}{7-1})\) = -1
=> (x-4)(4) = (-1)(8)(6)
=> x-4 = -12 => x= -16.

15. The points A (1, 2), B (3, 5), C (7, 8) are collinear.
a) True
b) False
View Answer

Answer: b
Explanation: We know, slope of line joining two points (x₁, y₁) and (x₂, y₂) is given by(y₂-y₁)/(x₂-x₁).
Slope of line AB = (5-2)/(3-1) = 3/2
Slope of line BC = (8-5)/(7-3) = 3/4
Since slope of AB is not equal to BC so, points are not collinear.

Sanfoundry Global Education & Learning Series – Mathematics – Class 11.

To practice all chapters and topics of class 11 Mathematics, here is complete set of 1000+ Multiple Choice Questions and Answers.

If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]

« Prev - Class 11 Maths MCQ – Straight Lines

» Next - Class 11 Maths MCQ – General Equation of a Line

Related Posts:

Recommended Articles: