This set of Class 11 Maths Chapter 7 Multiple Choice Questions & Answers (MCQs) focuses on “Permutations and Combinations”. These MCQs are created based on the latest CBSE syllabus and the NCERT curriculum, offering valuable assistance for exam preparation.
1. Permutation is also known as selection.
a) True
b) False
View Answer
Explanation: Permutation is known as arrangement. Selection is another name for combinations.
It involves arrangement of letters, numbers, persons etc.
2. nPr = ________________
a) n!
b) \(\frac{n!}{r!}\)
c) \(\frac{n!}{(n-r)!}\)
d) \(\frac{n!}{(n-r)! r!}\)
View Answer
Explanation: Permutation is known as arrangement. nPr means arranging r objects out of n.
nPr = \(\frac{n!}{(n-r)!}\).
3. 6! = _____________
a) 24
b) 120
c) 720
d) 8
View Answer
Explanation: We know, n! = n.(n-1).(n-2).(n-3)…..
6! = 6.5.4.3.2.1 = 720.
4. \(\frac{7!}{5!}\) = ____________________
a) 7
b) 42
c) 230
d) 30
View Answer
Explanation: We know, n! = n.(n-1).(n-2).(n-3)…… = n(n-1)!
\(\frac{7!}{5!} = \frac{7.6!}{5!} = \frac{7.6.5!}{5!}\) = 7.6 = 42.
5. \(\frac{100}{10!} = \frac{1}{8!} + \frac{x}{9!}\). Find x.
a) 1
b) 2
c) 3
d) 4
View Answer
Explanation: \(\frac{100}{10!} = \frac{1}{8!} + \frac{x}{9!}\).
We know, n! = n.(n-1). (n-2). (n-3) …………… = n(n-1)!
\(\frac{100}{10.9.8!} = \frac{1}{8!} + \frac{x}{9.8!}\)
=> \(\frac{100}{10.9} = \frac{1}{1} + \frac{x}{9}\)
=> \(\frac{10}{9} = 1 + \frac{x}{9}\)
=> \(\frac{x}{9} = \frac{10}{9} – 1 = \frac{1}{9}\)
=> x=1.
6. nP0 = ________________
a) n!
b) 1
c) \(\frac{1}{(n)!}\)
d) (n-1)!
View Answer
Explanation: We know, nPr = \(\frac{n!}{(n-r)!}\).
nP0 = \(\frac{n!}{(n-0)!} = \frac{n!}{(n)!}\) = 1.
7. nPn = ________________
a) n!
b) 1
c) \(\frac{1}{(n)!}\)
d) (n-1)!
View Answer
Explanation: We know, nPr = \(\frac{n!}{(n-r)!}\).
nPn = \(\frac{n!}{(n-n)!} = \frac{n!}{(0)!}\) = n!
8. The number of permutations of n different objects taken r at a time, where repetition is allowed is _______________
a) n!
b) r!
c) nPr
d) nr
View Answer
Explanation:
The number of permutations of n different objects taken r at a time, where repetition is allowed is n*n*n*n*n……………. r times = nr.
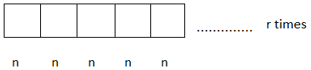
9. Find the number of permutations of word DEPENDENT.
a) 132400
b) 1512500
c) 1663200
d) 1723400
View Answer
Explanation: There are total 9 letters out of which 1T, 2N, 2D, 3E, 1P.
Total number of permutations are \(\frac{9!}{3!2!2!} = \frac{9.8.7.6.5.4.3.2.1}{6*2*2} = \frac{362880}{24}\) = 15120.
10. Find the number of 5 letter words which can be formed from word IMAGE without repetition using permutations.
a) 20
b) 60
c) 120
d) 240
View Answer
Explanation: IMAGE is a 5 letters word. We have to arrange all 5 letters of the word IMAGE without repetition. So, total permutations are nPr = 5P5 = 5! = 5.4.3.2.1 = 120.
11. Find the number of 5 letter words that can be formed from word IMAGE using permutations if repetition is allowed.
a) 25
b) 120
c) 125
d) 3125
View Answer
Explanation: IMAGE is a 5 letters word. We have to arrange all 5 letters of the word IMAGE with repetition allowed. So, total permutations are nr = 55 = 3125.
More MCQs on Class 11 Maths Chapter 7:
- Chapter 7 – Permutations and Combinations MCQ (Set 2)
- Chapter 7 – Permutations and Combinations MCQ (Set 3)
- Chapter 7 – Permutations and Combinations MCQ (Set 4)
To practice all chapters and topics of class 11 Mathematics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Practice Class 11 - Chemistry MCQs
- Practice Class 12 - Mathematics MCQs
- Practice Class 11 - Physics MCQs
- Practice Class 11 - Biology MCQs
- Check Class 11 - Mathematics Books
