This set of Class 11 Maths Chapter 1 Multiple Choice Questions & Answers (MCQs) focuses on “Operation on Sets – 1”.
1. If A = {1,2,3} and B = {3,4,5,6}. Find A∪B.
a) {1,2,3}
b) {3}
c) {1,2,3,4,5,6}
d) { }
View Answer
Explanation: Union of set A and B is a set that contains all the elements of set A and set B.
A = {1,2,3}
B = {3,4,5,6}
A∪B = {1,2,3,4,5,6}.
2. Let A be the set of odd numbers and B be the set of even numbers then find A∩B.
a) Set of prime numbers
b) Set of real numbers
c) Empty set
d) Set of natural numbers
View Answer
Explanation: Intersection of set A and B is a set that contains elements which is common to both set A and set B. Set of odd numbers and even numbers does not have any common element so, A∩B is an empty set.
3. If A={a, e, i, o, u} and B={a, e, u} then A∪B = __________
a) A
b) B
c) Φ
d) A∩B
View Answer
Explanation: Union of set A and B is a set that contains all the elements of set A and set B.
A={a, e, i, o, u}
B={a, e, u}
A∪B={a, e, i, o, u} = A.
4. If A = {a, e, i, o, u} and B = {a, e, u} then A∩B=__________
a) A
b) B
c) Φ
d) A∪B
View Answer
Explanation: Intersection of set A and B is a set that contains elements which is common to both set A and set B.
A = {a, e, i, o, u}
B = {a, e, u}
A∩B = {a, e, u} = B.
5. If A = {1,2,3} and B = {3,4,5,6}. Find A∩B.
a) {1,2,3}
b) { }
c) {1,2,3,4,5,6}
d) {3}
View Answer
Explanation: Intersection of set A and B is a set that contains elements which is common to both set A and set B.
A = {1,2,3}
B = {3,4,5,6}
Here, 3 is common to both sets so A∩B = {3}.
6. Is A∪B = B∪A?
a) True
b) False
View Answer
Explanation: Let A = {1,2} and B = {2,3}. Here A∪B = {1,2,3} = B∪A.
A∪B or B∪A is same set that contains all the elements of set A and set B.
7. Is A∩B = B∩A?
a) True
b) False
View Answer
Explanation: Let A = {1,2} and B = {2,3}. Here A∩B = {2} = B∩A.
A∩B or B∩A is same set that contains elements which are common to both set A and B.
8. In the given Venn diagram, find A∪B.
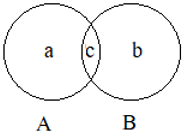
a) a
b) b
c) a + c
d) a + b + c
View Answer
Explanation: Union of two sets A and B is the region that includes entire set A and set B.
In the given Venn diagram, A∪B is region a + b + c.
9. In the given Venn diagram, find A∩B.

a) a
b) b
c) c
d) a + b + c
View Answer
Explanation: Intersection of two sets A and B is the region common to both set A and set B.
In the given Venn diagram, common region is c so, A∩B is region c.
10. In the given Venn diagram, find A∪B.
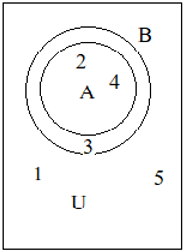
a) {1,2,3}
b) {2,4}
c) {3}
d) {2,3,4}
View Answer
Explanation: Union of two sets A and B is the region that includes entire set A and set B.
In the given Venn diagram, A∪B={2,3,4}.
11. In the given Venn diagram, find A∩B.

a) {1,2,3}
b) {2,4}
c) {3}
d) {2,3,4}
View Answer
Explanation: Intersection of two sets A and B is the region common to both set A and set B.
In the given Venn diagram, A∩B={2,4}.
Sanfoundry Global Education & Learning Series – Mathematics – Class 11.
To practice all chapters and topics of class 11 Mathematics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Practice Class 11 - Biology MCQs
- Practice Class 12 - Mathematics MCQs
- Check Class 11 - Mathematics Books
- Practice Class 11 - Physics MCQs
- Practice Class 11 - Chemistry MCQs
