This set of Class 11 Maths Chapter 1 Multiple Choice Questions & Answers (MCQs) focuses on “Practical Problems on Union and Intersection of Two Sets”.
1. Which of the following is correct?
a) n (A ∪ B) = n (A) + n (B) + n (A ∩ B)
b) n (A ∪ B) = n (A) – n (B) – n (A ∩ B)
c) n (A ∪ B) = n (A) + n (B) – n (A ∩ B)
d) n (A ∩ B) = n (A) + n (B) + n (A ∪ B)
View Answer
Explanation: In the Venn diagram,
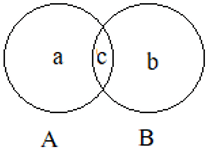
n (A ∪ B) = a + b + c
n(A) = a + c, n(B) = b + c and n (A ∩ B) = c
n (A) + n (B) – n (A ∩ B) = (a + c) + (b + c)-c = a + b + c.
Hence, n (A ∪ B) = n (A) + n (B) – n (A ∩ B).
2. What is A ∪ B for two mutually exclusive sets A and B?
a) n (A) + n (B)
b) n (A) – n (B)
c) n (B) – n (A)
d) n (A) * n (B)
View Answer
Explanation: We know, n (A ∪ B) = n (A) + n (B) – n (A ∩ B).
For mutually exclusive sets A ∩ B=Φ i.e. n (A ∩ B)=0.
n (A ∪ B) = n (A) + n (B).
3. If set A has 10 elements, set B has 20 elements, 5 elements are common to both then find the number of elements in X∪Y.
a) 10
b) 15
c) 20
d) 25
View Answer
Explanation: We know, n (A ∪ B) = n (A) + n (B) – n (A ∩ B)
Given, n (A) = 10, n (B) = 20, n (A ∩ B) = 5.
n (A ∪ B) = 10 + 20 – 5 = 25.
4. In a family of 10 members, 7 of them like tea or coffee, 4 of them like tea and 5 of them like coffee. How many of them like both tea and coffee?
a) 1
b) 2
c) 7
d) 9
View Answer
Explanation: We know, n (T ∪ C) = n (T) + n (C) – n (T ∩ C)
Given, n (T ∪ C) = 7, n(T)=4, n(C)=5
7 = 4 + 5 – n (T ∩ C)
n (T ∩ C) = 2.
Hence, 2 members like both tea and coffee.
5. In a family of 10 members, 7 of them like tea or coffee, 4 of them like tea and 5 of them like coffee. How many of them like neither tea nor coffee?
a) 1
b) 2
c) 3
d) 4
View Answer
Explanation: Given, n (T ∪ C) = 7.
By de Morgan’s law, n (T’ ∩ C’) = n (T ∪ C)’ = Total – n (T ∪ C) = 10 – 7 = 3.
So, 3 members like neither tea nor coffee.
6. In a family of 10 members, 7 of them like tea or coffee, 4 of them like tea and 5 of them like coffee. How many of them like only tea?
a) 2
b) 3
c) 4
d) 5
View Answer
Explanation: We know, n (T ∪ C) = n (T) + n (C) – n (T ∩ C)
Given, n (T ∪ C) = 7, n(T)=4, n(C)=5
7=4+5- n (T ∩ C)
n (T ∩ C) = 2.
n (only T) = n (T ∩ C’) = n (T)- n (T ∩ C) = 4-2=2.
2 members like only tea.
7. In a family of 10 members, 7 of them like tea or coffee, 4 of them like tea and 5 of them like coffee. How many of them like only coffee?
a) 2
b) 3
c) 4
d) 5
View Answer
Explanation: We know, n (T ∪ C) = n (T) + n (C) – n (T ∩ C)
Given, n (T ∪ C) = 7, n(T)=4, n(C)=5
7=4+5- n (T ∩ C)
n (T ∩ C) = 2.
n (only C) = n (C ∩ T’) = n (C) – n (T ∩ C) = 5-2=3.
3 members like only coffee.
8. In a city of 1000 population, all people read newspaper. 600 people read Hindustan Times and 700 people read Times of India. How many people read both newspaper?
a) 100
b) 300
c) 1000
d) 1300
View Answer
Explanation: Since all people read newspaper so, n (T ∪ H) = 1000.
n(H) = 600 and n(T) = 700.
n (T ∪ H) = n (T) + n (H) – n (T ∩ H)
1000 = 700 + 600 – n (T ∩ H)
n (T ∩ H) = 1300-1000 = 300.
9. In a city of 1000 population, all people read newspaper. 600 people read Hindustan Times and 700 people read Times of India. How many people read only Hindustan Times?
a) 100
b) 200
c) 300
d) 600
View Answer
Explanation: Since all people read newspaper so, n (T ∪ H) = 1000.
n(H) = 600 and n(T) = 700.
n (T ∪ H) = n (T) + n (H) – n (T ∩ H)
1000 = 700 + 600 – n (T ∩ H)
n (T ∩ H) = 1300-1000 = 300.
n (T’ ∩ H) = n(H)- n (T ∩ H) = 600-300 = 300.
300 persons read only Hindustan Times.
10. In a city of 1000 population, all people read newspaper. 600 people read Hindustan Times and 700 people read Times of India. How many people read only Times of India?
a) 200
b) 400
c) 600
d) 700
View Answer
Explanation: Since all people read newspaper so, n (T ∪ H) = 1000.
n(H) = 600 and n(T) = 700.
n (T ∪ H) = n (T) + n (H) – n (T ∩ H)
1000 = 700 + 600 – n (T ∩ H)
n (T ∩ H) = 1300-1000 = 300.
n (T ∩ H’) = n (T) – n (T ∩ H) = 700-300 = 400.
400 persons read only Hindustan Times.
11. In a committee, if 50 people speak French, 20 people speak Spanish, 10 people speak both the languages, then how many people speak at least one of the two languages?
a) 10
b) 20
c) 50
d) 60
View Answer
Explanation: We know, n (F∪S) = n (F) + n (S) – n(F∩S)
Given, n (F)=50, n (S)=20, n (F∩S) = 10
n (F∪S) = 50 + 20 – 10 = 60.
60 people speak at least one of the two languages.
12. A group conducted a survey of 100 consumers and reported that 72 consumers like apples and 45 consumers like oranges, what is the least number that must have liked both products?
a) 14
b) 15
c) 16
d) 17
View Answer
Explanation: n(U)=100, n(A)=72, n(O)=45
n (A∪O) = n (A) + n (O) – n(A∩O)
n (A∪O) ≤ n(U) => n (A∪O) ≤ 100
Greatest value of n (A∪O) is 100 which gives least value of n(A∩O)
100=72+45 – n(A∩O)
n(A∩O) = 17 least value of n(A∩O).
13. In a population of 1000 people, 700 people play football, 600 people play cricket, and 100 people play both. Is the data correct?
a) True
b) False
View Answer
Explanation: Given, n(U)=1000, n(F)=700, n(C)=600, n(F∩C) =100
n (F∪C) = n (F) + n (C) – n(F∩C)
n (F∪C) = 700+600-100=1200
We know, n (A∪O) ≤ n(U). Here this is not valid so, data is incorrect.
14. In a group of students, 100 students know Hindi, 50 know English and 25 know both. Each of the student knows either Hindi or English. How many students are there in the group?
a) 75
b) 100
c) 125
d) 175
View Answer
Explanation: Given, n(H)=100, n(E)=50, n(H∩E) = 25
We know, n (H∪E) = n (H) + n (E) – n(H∩E)
n (H∪E) = 100+50-25=125
Since each of the student knows either Hindi or English, so n(U) = n (H∪E) = 125.
15. If 200 people like tea, 300 people like coffee and 250 people like both. Is the data correct?
a) True
b) False
View Answer
Explanation: Given, n(T)=200, n(C)=300, n(T∩C) = 250
We know, n(T∩C) ≤ n(T) and n(T∩C) ≤ n(C)
But here n(T∩C) ≤ n(T) is not valid so, data given is incorrect.
Sanfoundry Global Education & Learning Series – Mathematics – Class 11.
To practice all chapters and topics of class 11 Mathematics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Practice Class 11 - Physics MCQs
- Practice Class 11 - Chemistry MCQs
- Check Class 11 - Mathematics Books
- Practice Class 12 - Mathematics MCQs
- Practice Class 11 - Biology MCQs
