This set of Class 11 Maths Chapter 1 Multiple Choice Questions & Answers (MCQs) focuses on “Operation on Sets – 2”.
1. If set A={1,2,3,4} and B={3,4,5,6}. Find A-B.
a) {1,2,3,4,5,6}
b) {3,4}
c) {1,2}
d) {5,6}
View Answer
Explanation: A-B is the set of elements that belongs to A but not to B. Here, 1 and 2 belongs to A but not to B. So,
A = {1,2,3,4}
B = {3,4,5,6}
A – B = {1,2,3,4} – {3,4,5,6} = {1,2}.
2. If set A = {1,2,3,4} and B = {3,4,5,6}. Find B-A.
a) {1,2,3,4,5,6}
b) {3,4}
c) {1,2}
d) {5,6}
View Answer
Explanation: B-A is the set of elements that belongs to B but not to A. Here, 5 and 6 belongs to B but not to A. So,
A = {1,2,3,4}
B = {3,4,5,6}
B-A = {3,4,5,6} – {1,2,3,4} = {5,6}.
3. Does A-B=B-A always correct?
a) True
b) False
View Answer
Explanation: If A={1,2,3} and B={3,4,5}, then A-B={1,2,3} – {3,4,5} = {1,2} and B-A={3,4,5} – {1,2,3} = {4,5}. They are not equal so,
A-B and B-A are not always equal.
4. If A-B=B-A then A and B are ____________
a) equivalent sets
b) equal sets
c) disjoint sets
d) empty sets
View Answer
Explanation: A-B is the set of elements that belongs to A but not to B and B-A is the set of elements that belongs to B but not to A. A-B=B-A is possible only when A and B are equal sets.
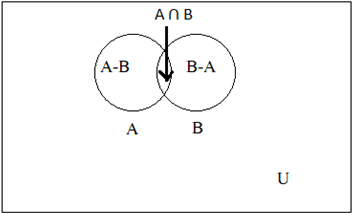
5. A – B, A ∩ B and B – A are mutually disjoint sets or not.
a) True
b) False
View Answer
Explanation: A – B, A ∩ B and B – A does not have any common region so the intersection of any two of them is null set. So, they are said to be mutually disjoint.
6. If R is the set of real numbers and S is the set of rational numbers, then what is R – S?
a) Set of integers
b) Set of whole numbers
c) Set of irrational numbers
d) Set of complex numbers
View Answer
Explanation: There are two categories in real numbers which are rational and irrational. The real number which is not rational is irrational so, R-S denotes the set of irrational numbers.
7. A={1,2,3}, B={2,3,4}, C={2,3,5}, D={1,3,5,7}. Find (A∪B) ∩ (C∪D).
a) A
b) B
c) C
d) D
View Answer
Explanation: Here, A={1,2,3}, B={2,3,4}, C={2,3,5}, D={1,3,5,7}
A∪B={1,2,3}∪{2,3,4} = {1,2,3,4} and C∪D={2,3,5}∪{1,3,5,7} = {1,2,3,5,7}
(A∪B) ∩ (C∪D) = {1,2,3,4} ∩ {1,2,3,5,7} = {1,2,3} = A.
8. A={1,2,3}, B={2,3,4}, C={2,3,5}, D={1,3,5,7}. Find (A∩B) ∪ (C∩D).
a) A
b) B
c) C
d) D
View Answer
Explanation: Here, A={1,2,3}, B={2,3,4}, C={2,3,5}, D={1,3,5,7}
A∩B = {1,2,3}∩{2,3,4} = {2,3} and C∩D = {2,3,5}∩{1,3,5,7} = {3,5}.
(A∩B) ∪ (C∩D) = {2,3} ∪ {3,5} = {2,3,5} = C.
9. If A is set of natural numbers, B is set of odd natural numbers and C is set of even natural numbers, then find A-B.
a) A
b) B
c) C
d) B-C
View Answer
Explanation: Natural number which is not odd is even. A-B means set of natural numbers excluding odd natural numbers so, A-B is set of even natural numbers Hence, A-B=C.
10. If A is set of natural numbers, B is set of odd natural numbers and C is set of even natural numbers, then find B∪C.
a) A
b) B
c) C
d) B-C
View Answer
Explanation: Set which contains all odd natural numbers as well as all even natural numbers is set of natural numbers. So, B∪C=A.
11. If A is set of natural numbers, B is set of odd natural numbers and C is set of even natural numbers, then find B∩C.
a) A
b) B
c) C
d) Φ
View Answer
Explanation: Set of odd natural numbers and set of even natural numbers doesn’t have any common element as a natural number cannot be both odd and even. So, B∩C=Φ.
12. (A∪B) ∩ (B∪A) = __________
a) A
b) B
c) A∪B
d) A∩B
View Answer
Explanation: (A∪B) ∩ (B∪A) = (A∪B) ∩ (A∪B) (Commutative law)
= A∪B (A∩A=A).
13. (A∩B) ∪ (B∩A) = ______________
a) A
b) B
c) A∪B
d) A∩B
View Answer
Explanation: (A∩B) ∪ (B∩A) = (A∩B) ∪ (A∩B) (Commutative law)
= A∩B (A∪A=A).
Sanfoundry Global Education & Learning Series – Mathematics – Class 11.
To practice all chapters and topics of class 11 Mathematics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Practice Class 11 - Chemistry MCQs
- Practice Class 11 - Biology MCQs
- Practice Class 12 - Mathematics MCQs
- Check Class 11 - Mathematics Books
- Practice Class 11 - Physics MCQs
