This set of Class 11 Maths Chapter 2 Multiple Choice Questions & Answers (MCQs) focuses on “Functions”.
1. In a function from set A to set B, every element of set A has___________ image in set B.
a) one and only one
b) different
c) same
d) many
View Answer
Explanation: A relation from a set A to a set B is said to be a function if every element of set A has one and one image in set B.
2. In a function from set A to set B, image can have more than one preimage.
a) True
b) False
View Answer
Explanation: A relation from a set A to a set B is said to be a function if every element of set A has one and one image in set B. A preimage must have one image, an image can have more than one preimage.
3. Let R be a relation defined on set of natural numbers {(x, y): y=2x}. Is this relation can be called a function?
a) True
b) False
View Answer
Explanation: Since every natural number has one and only image so this relation can be called a function.
4. Which of the following is not a function?
a) {(1,2), (2,4), (3,6)}
b) {(-1,1), (-2,4), (2,4)}
c) {(1,2), (1,4), (2,5), (3,8)}
d) {(1,1), (2,2), (3,3)}
View Answer
Explanation: A relation from a set A to a set B is said to be a function if every element of set A has one and one image in set B.
In {(1,2), (1,4), (2,5), (3,8)}, since element 1 has two images 2 and 4 which is not possible in a function so, it is not a function. Rest all have one and only one image so they can be called a function.
5. Which function is shown in graph?
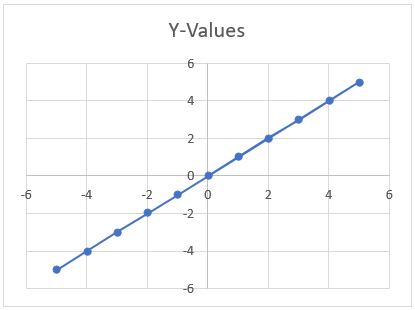
a) Constant
b) Modulus
c) Identity
d) Signum function
View Answer
Explanation: {(1,1), (2,2), (3,3), …..}. This function involves relation {(x, y): y=x} which is involved in identity function. So, above function is identity function.
6. Which function is shown in graph?
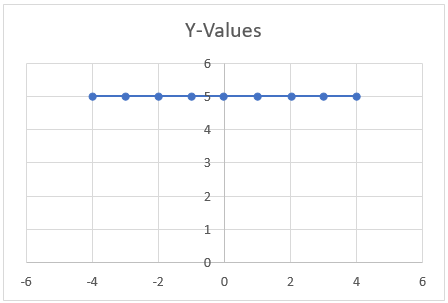
a) Constant
b) Modulus
c) Identity
d) Signum function
View Answer
Explanation: {(1,5), (2,5), (3,5),……}. This function involves relation {(x, y): y=constant} which is involved in constant function. So, above function is constant function.
7. Which function is shown in graph?
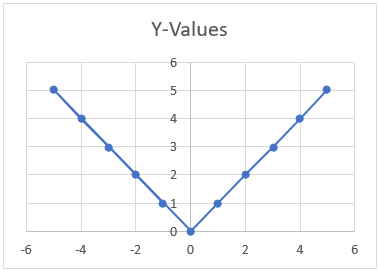
a) Constant
b) Modulus
c) Identity
d) Signum function
View Answer
Explanation: {(-1,1), (1,1), (-2,2), (2,2), (-3,3), (3,3), ……}. This function involves relation {(x, y): y = |x|} which is involved in modulus function. So, above function is modulus function.
8. f(x) = {\(\frac{|x|}{x}\) for x≠0 and 0 for x=0}. Which function is this?
a) Constant
b) Modulus
c) Identity
d) Signum function
View Answer
Explanation: f(x) = {\(\frac{|x|}{x}\) for x≠0 and 0 for x=0}. Function is {(-3, -1), (-2, -1), (-1,1), (0,0), (1,1), (2,1), (3,1), …….}. This is signum function.
9. Find domain of function |x|.
a) Set of real numbers
b) Set of positive real numbers
c) Set of integers
d) Set of natural numbers
View Answer
Explanation: Since the above function can have all real values of x. So, domain is set of real numbers.

10. Find range of function |x|.
a) Set of real numbers
b) Set of positive real numbers
c) Set of integers
d) Set of natural numbers
View Answer
Explanation: Since the above function can have positive real value of y for all real values of x. So, range is set of positive real numbers.

11. f(x) = \(\sqrt{9-x^2}\). Find the domain of the function.
a) (0,3)
b) [0,3]
c) [-3,3]
d) (-3,3)
View Answer
Explanation: We know radical cannot be negative. So, 9-x,2 ≥ 0
(3-x) (3+x) ≥ 0 => (x-3) (x+3) ≤ 0 => x∈[-3,3].
12. f(x) = \(\sqrt{9-x^2}\). Find the range of the function.
a) R
b) R+
c) [-3,3]
d) [0,3]
View Answer
Explanation: We know, square root is always non-negative. So, \(\sqrt{9-x^2}\) ≥ 0. So, the range of the function is set of positive real numbers from 0 to 3.
Sanfoundry Global Education & Learning Series – Mathematics – Class 11.
To practice all chapters and topics of class 11 Mathematics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Practice Class 11 - Physics MCQs
- Practice Class 12 - Mathematics MCQs
- Check Class 11 - Mathematics Books
- Practice Class 11 - Biology MCQs
- Practice Class 11 - Chemistry MCQs
