This set of Class 11 Maths Chapter 3 Multiple Choice Questions & Answers (MCQs) focuses on “Trigonometric Equations – 2”.
1. Which of the following will form the following graph?
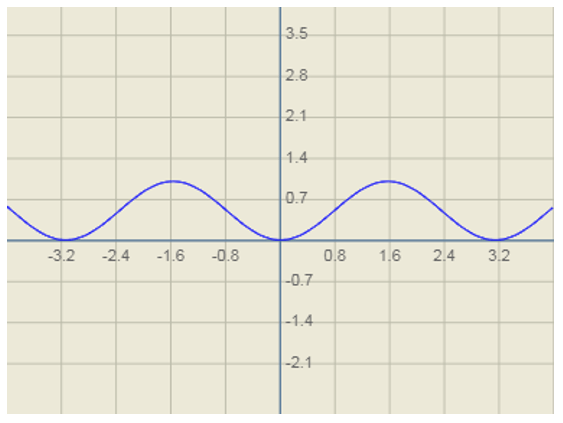
a) sinx + cosx
b) 2sin(x/2)
c) sin2x
d) cosec(x2)
View Answer
Explanation:
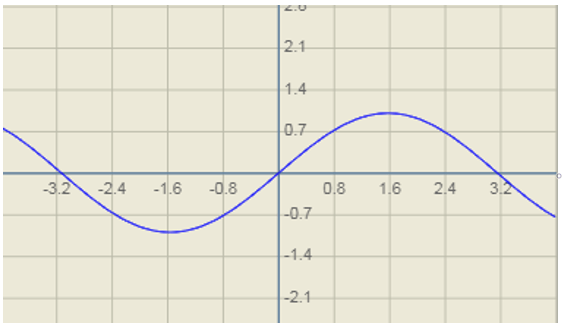
This is the curve of sinx.
It is given that the graph in the question does not lay in the –y axis.
So, when we plot the graph of sin2x the part laying in the –y axis comes in the positive y axis.
2. What is the value of tanθ?
a) √(1 + cos2θ)/cosθ
b) √(1 – cos2θ)/cosθ
c) (√(1 – cos2θ))cosθ
d) √(1 – cos2θ)+cosθ
View Answer
Explanation: If AOB is a righted angled triangle with ∠AOB = θ and ∠BAO = 90°
Also, consider OA = x and OB = 1
By definition, cosθ = OA/OB = x/1 = x
So, AB = √(1 – x2)
By definition, AB/OA = √(1 – x2)/x
= √(1 – cos2θ)/cosθ.
3. What will be the value of (sinx + cosecx)2 + (cosx + secx)2 ?
a) ≥ 0
b) ≤ 0
c) ≤ 1
d) ≥ 1
View Answer
Explanation: The given expression in LHS is,
sin2x + cosec2x + 2 + cos2x + sec2x + 2
4 + (sin2x + cos2x) +(1 + tan2x) + (1 + cot2x)
= 7 + (tan2x + cot2x)
= 7 + (tanx – cotx)2 + 2 which is ≥ 0.
4. What will be the value of dy/dx = (x + 2y + 3)/(2x + 3y + 4)?
a) -2π – 9
b) 2π – 9
c) -2π + 9
d) 2π + 9
View Answer
Explanation: We know, sec x = sec(π – x)
So, sec 6 = sec(π – 9)
= sec(2π + 9)
= sec(3π – 9)
= sec(-π – 9)
= sec(-2π – 9)
= sec(-3π – 9)
So, sec-1(sin 9) = sin-1(sin (-2π + 9))
= -2π + 9.
5. Which one is correct for Napier’s Analogy?
a) tan (C/2) = (a + b)/(a – b) (tan(A – B)/2)
b) tan (C/2) = (a – b)/(a + b) (cot(A – B)/2)
c) tan (C/2) = (a – b)/(a + b) (cot(A + B)/2)
d) tan (C/2) = (a + b)/(a – b) (tan(A + B)/2)
View Answer
Explanation: According to the law of sines, in any triangle ABC,
a/sinA = b/sinB = c/sinC
So, a/b = sinA/sinB
(a + b)/(a – b) = (sinA + sinB)/( sinA – sinB)
=> (a + b)/(a – b) = (2 sin((a + b)/2) cos((a – b)/2))/ (2 sin((a + b)/2) sin((a – b)/2))
=> (a + b)/(a – b) = (tan(A + B)/2)/(tan(A – B)/2)
=> (tan(A + B)/2) = (a + b)/(a – b) (tan(A – B)/2)
=> (tan(π/2 + C/2)) = (a + b)/(a – b) (tan(A – B)/2)
=> cot (C/2) = (a + b)/(a – b) (tan(A – B)/2)
=> tan (C/2) = (a – b)/(a + b) (cot(A – B)/2).
6. What is the value of (1 + cotA)(1 + cotB) for isosceles right triangle ABC right angled at A?
a) 0
b) 1
c) 2
d) Data inadequate
View Answer
Explanation: (1 + cotA)(1 + cotB)
Simplifying the above equation,
= 1 + cotA + cotB + cotAcotB
Putting the values of A and B, we get,
= 1 + cot90 + cot45 + cot90cot45
= 1 + 0 + 1 + 0
= 2.
7. Which one is correct for Napier’s Analogy?
a) tan (A/2) = (b – c)/(b + c) (tan(B + C)/2)
b) tan (A/2) = (b – c)/(b + c) (cot(B – C)/2)
c) tan (A/2) = (b + c)/(b – c) (cot(B – C)/2)
d) tan (A) = (b – c)/(b + c) (tan(B – C)/2)
View Answer
Explanation: According to the law of sines, in any triangle ABC,
a/sinA = b/sinB = c/sinC
So, a/b = sinA/sinB
(a + b)/(a – b) = (sinA + sinB)/( sinA – sinB)
=> (a + b)/(a – b) = (2 sin((a + b)/2) cos((a – b)/2))/ (2 sin((a + b)/2) sin((a – b)/2))
=> (a + b)/(a – b) = (tan(A + B)/2)/(tan(A – B)/2)
=> (tan(A + B)/2) = (a + b)/(a – b) (tan(A – B)/2)
=> (tan(π/2 + C/2)) = (a + b)/(a – b) (tan(A – B)/2)
=> cot (C/2) = (a + b)/(a – b) (tan(A – B)/2)
=> tan (C/2) = (a – b)/(a + b) (tan(A – B)/2)
Similarly, tan (A/2) = (b – c)/(b + c) (cot(B – C)/2).
8. Which one is correct for Napier’s Analogy?
a) tan (B/2) = (c – a)/(c + a) (cot(C + A)/2)
b) tan (B/2) = (c – a)/(c + a) (cot(C – A)/2)
c) tan (B/2) = (c + a)/(c – a) (cot(C – A)/2)
d) tan (B) = (c – a)/(c + a) (cot(C – A)/2)
View Answer
Explanation: According to the law of sines, in any triangle ABC,
a/sinA = b/sinB = c/sinC
So, a/b = sinA/sinB
(a + b)/(a – b) = (sinA + sinB)/( sinA – sinB)
=> (a + b)/(a – b) = (2 sin((a + b)/2) cos((a – b)/2))/ (2 sin((a + b)/2) sin((a – b)/2))
=> (a + b)/(a – b) = (tan(A + B)/2)/(tan(A – B)/2)
=> (tan(A + B)/2) = (a + b)/(a – b) (tan(A – B)/2)
=> (tan(π/2 + C/2)) = (a + b)/(a – b) (tan(A – B)/2)
=> cot (C/2) = (a + b)/(a – b) (tan(A – B)/2)
=> tan (C/2) = (a – b)/(a + b) (cot(A – B)/2)
Similarly, tan (B/2) = (c – a)/(c + a) (cot(C – A)/2).
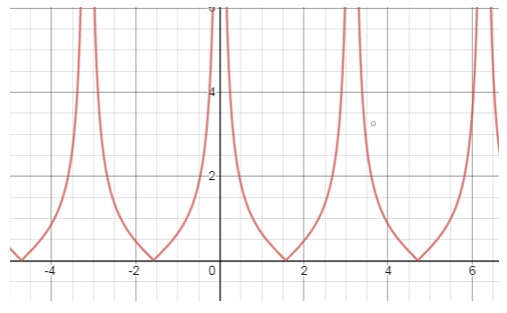
9. The given graph is for which equation?
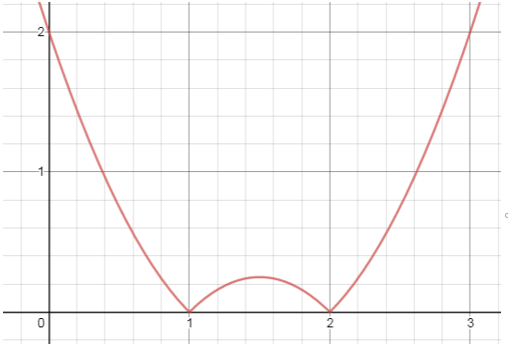
a) y = (x – 1)(x – 2)
b) y = (x + 1)(x + 2)
c) y = |(x – 1)(x – 2)|
d) y = |(x + 1)(x + 2)|
View Answer
Explanation: As the critical points are 1and 2 so the graph will form in this range only.
Clearly, as the equation is enclosed in modulus so,
The graph will lie in the positive y direction and will approach infinity.
10. The given graph is for which equation?
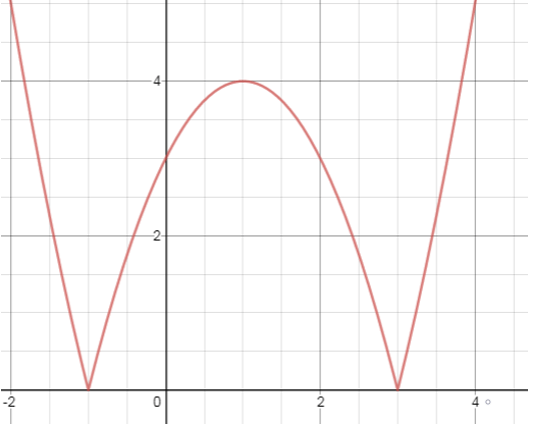
a) y = |(x + 1)(x – 3)|
b) y = |(x + 1)(x + 3)|
c) y = |(x – 1)(x – 3)|
d) y = -|(x + 1)(x – 3)|
View Answer
Explanation: As, the critical points are -1 and 3,
Therefore, the curve will lie from (-1, 3)
So, this curve will cut the positive y axis at y = 3 and reach to the maximum height and come to point 3 at positive x axis.
Generally it attains a maximum height of 4 units in positive y axis.
As, the equation is enclosed by modulus so, it will lie only to upper y axis.
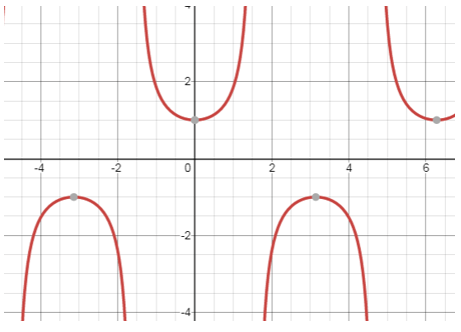
11. The given graph is for which equation?
a) cosecx
b) cotx
c) secx
d) cosx
View Answer
Explanation: There are 2 curves.
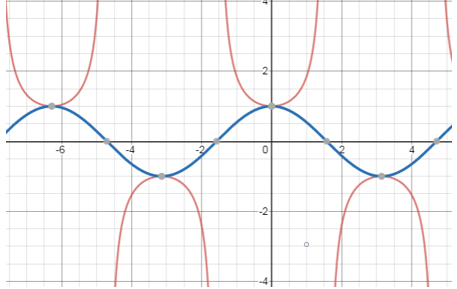
The blue curve is the graph of y = cosx
The red curve is the graph for y = secx
As, secx is reciprocal of cosx, so,
The graph of secx is the reciprocal of the graph of cosx.
So, the point at which cosx attain maximum height i.e. 1 and -1 in positive and negative y axis is the point of origin of this graph that approaches to infinity.
12. The given graph is for which equation?
a) |sinx|
b) |cotx|
c) |sinx|
d) Unpredictable
View Answer
Explanation: The above graph is for |cotx|
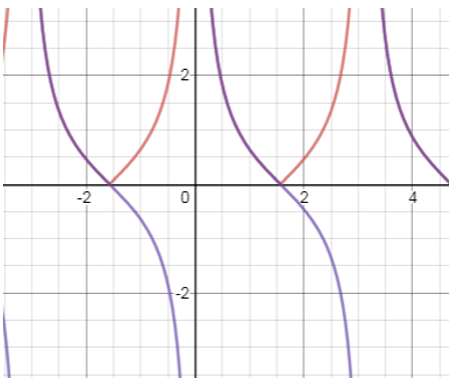
The blue curve is for y = cotx and red line is for |cotx|
As, half the part of graph is below x axis is negative so, due to modulus it moves to above x axis.
The graph approaches to infinity.
Sanfoundry Global Education & Learning Series – Mathematics – Class 11.
To practice all chapters and topics of class 11 Mathematics, here is complete set of 1000+ Multiple Choice Questions and Answers.
- Practice Class 11 - Biology MCQs
- Check Class 11 - Mathematics Books
- Practice Class 12 - Mathematics MCQs
- Practice Class 11 - Physics MCQs
- Practice Class 11 - Chemistry MCQs
