This set of Finite Element Method Multiple Choice Questions & Answers (MCQs) focuses on “Beams with Uniformly Distributed Load”.
1. The magnitude of resultant force of a Distributed Loading is equal to half the area under its curve.
a) True
b) False
View Answer
Explanation: Distributed Loading problems can be solved using two methods. They are Geometry method and the Integral Method. In the Geometry method of solving, the magnitude of resultant force of the Distributed Loading is equal to the area under its curve. Whereas, in the Integral method, the magnitude of resultant force of the Distributed Loading is given by the integral of the curve defining this load.
2. Which type of loading is depicted in the figure below?
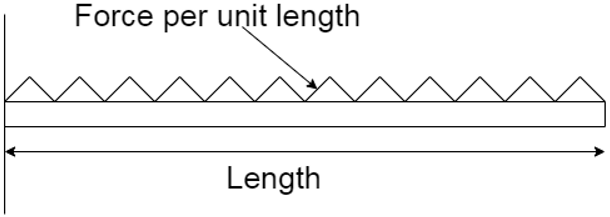
a) Axial
b) Bending
c) Torsion
d) Uniformly Distributed Load
View Answer
Explanation: Uniformly Distributed Load is the type of loading depicted in the figure. It is a type of load whose magnitude remains constant across the length of the structure under discussion. Axial Load and Torsion Load are types of loading where the force acts along the axis of the structure. In bending load, the force acts perpendicular to the axis of the structure under discussion.
3. What is the bending moment of a cantilever beam subjected to Uniformly Distributed Load? Assume length of beam = L; load = w per unit length.
a) wL
b) wL / 2
c) wL2 / 2
d) wL2 / 4
View Answer
Explanation: We know that, bending moment at any given section is proportional to the square of the distance of the section from the free end.
Therefore,
Bending moment = total load * Distance of CG
= (wL) * (L / 2)
= wL2 / 2
4. Find out the bending moment of a cantilever beam subjected to Uniformly Distributed Load. Given – length of beam = 5m, load = 100N / m.
a) 12500Nm
b) 1250Nm
c) 125Nm
d) 12.5KNm
View Answer
Explanation: Load (w) = 100N / m; Length = 5m
We know that, bending moment = wL2 / 2
= (100 * (5)2) / 2
= 1250Nm
5. What is the expression for maximum deflection for a cantilever beam subjected to Uniformly Distributed Load? Assume load = w (N / m), length of beam = l.
a) wl4 / 8EI
b) wl2 / 8EI
c) wl3 / 8EI
d) wl / 8EI
View Answer
Explanation: The expression for maximum deflection for a cantilever beam subjected to Uniformly Distributed Load is given by – wl4 / 8EI; where w = load acting, l = length of beam, E = Young’s Modulus and I = Moment of Inertia.
6. Find out the maximum deflection of a cantilever beam subjected to Uniformly Distributed Load. Given load = 1000N, length of beam = 8.5m, moment of inertia of the beam = 5000mm4. Assume Young’s Modulus = 210 GPa.
a) 587.05m
b) 436.28m
c) 621.43m
d) 104.37m
View Answer
Explanation: Load (w) = 1000N, Length (l) = 8.5m, Moment of Inertia (I) = 5000mm4, Young’s Modulus (E) = 210Gpa
We know that max deflection = wl4 / 8EI
= (1000 * (8.5)4) / (8 * 5 * 10-9 * 210 * 109)
= 621.43m
7. What is the expression for maximum deflection for a simple supported beam subjected to Uniformly Distributed Load? Assume load = w (N / m), length of beam = l.
a) wl3 / 38EI
b) 5wl4 / 384EI
c) wl4 / 384EI
d) 8wl4 / 384EI
View Answer
Explanation: The expression for maximum deflection for a simply supported beam subjected to Uniformly Distributed Load is given by – 5wl4 / 384EI; where w = load acting, l = length of beam, E = Young’s Modulus and I = Moment of Inertia.
8. Find out the maximum deflection of a simply supported beam subjected to Uniformly Distributed Load. Given load = 500N, length of beam = 10m, moment of inertia of the beam = 8000mm4. Assume Young’s Modulus = 210 GPa.
a) 236.48m
b) 148.76m
c) 58.97m
d) 38.75m
View Answer
Explanation: Load (w) = 500N, Length (l) = 10m, Moment of Inertia (I) = 8000mm4, Young’s Modulus (E) = 210Gpa
We know that max deflection = 5wl4 / 384EI
= (5 * 500 * 104) / (384 * (8 * 10-9) * 210 * 109)
= 38.75m
9. Galerkin approach is a method used for imposing boundary conditions.
a) False
b) True
View Answer
Explanation: Galerkin method is used for solving differential equations. However, there are two methods of imposing boundary conditions. They are Elimination approach and Penalty approach. In elimination approach, the known value of displacement is removed from list of unknowns and the number of equations are reduced. In penalty approach, Round off errors involved in computations is advantageously used to impose boundary conditions.
10. Which of the following approach is used to calculate stresses caused due to change in temperature?
a) Penalty Approach
b) Elimination Approach
c) Galerkin Approach
d) Variational Approach
View Answer
Explanation: Variational Approach is one of the two approaches used to calculate stresses caused due to change in temperature. This approach is a graphical method where strain due to change in temperature is treated as initial strain. The other approach used is the Direct Approach, which is a non graphical method and makes use of governing equations to solve the problem.
Sanfoundry Global Education & Learning Series – Finite Element Method.
To practice all areas of Finite Element Method, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Check Civil Engineering Books
- Apply for Civil Engineering Internship
- Apply for Mechanical Engineering Internship
- Practice Civil Engineering MCQs
- Practice Mechanical Engineering MCQs
