This set of Finite Element Method Multiple Choice Questions & Answers (MCQs) focuses on “ Classical Plate Model”.
1. In FEM, what does the simple two-dimensional plate theories account for?
a) The kinematics of bending deformation of thin bodies without to transverse loads
b) The kinematics of bending deformation of thin bodies subjected to transverse loads
c) Thin bodies subjected to transverse loads without bending deformation
d) Thin plates subjected to transverse loads with bending deformation
View Answer
Explanation: The term “plate” refers to solid bodies that are bounded by two parallel planes whose lateral dimensions are large compared with the separation between them (i.e., the thickness of the plate). In most cases, the thickness is no greater than one-tenth of the smallest in-plane dimension. Geometrically, plate problems are similar to the plane stress problems except that plates are also subjected to transverse loads. Thus, the simple two-dimensional plate theories account for the kinematics of bending deformation of thin bodies subjected to transverse loads.
2. In the bending of elastic plates, although the plate problems are similar to the plane stress problems, plates are also subjected to transverse loads that cause bending about axes normal to the plane of the plate.
a) True
b) False
View Answer
Explanation: A plate is a solid body that is bounded by two parallel planes whose lateral dimensions are large compared with the separation between them (i.e., the thickness of the plate). Mostly, the thickness is lesser than one-tenth of the smallest in-plane dimension. Geometrically, plate problems are similar to the plane stress problems except that plates are also subjected to transverse loads (i.e., loads perpendicular to the plane of the plate) that cause bending about axes in the plane of the plate.
3. Which option is correct about an analog of a plate in simple plate theory used in FEM?
a) A plate is a one-dimensional analog of a beam
b) A plate is a two-dimensional analog of a beam
c) A plate is a three-dimensional analog of a beam
d) A plate is not analogous to beam
View Answer
Explanation: Geometrically, plate problems are similar to the plane stress problems except that plates are also subjected to transverse loads that cause bending about axes in the plane of the plate. In other words, a plate is a two-dimensional analog of a beam. Because of the smallness of the thickness dimension, it is often not necessary to model plates using three-dimensional elasticity theory. Simple two-dimensional theories that account for the kinematics of bending deformation of thin bodies subjected to transverse loads have been developed, and they are known as plate theories.
4. In FEM, which principle is used to derive the governing equations of displacement-based plate theories?
a) The principle of virtual forces
b) The principle of virtual work
c) The principle of virtual displacements
d) The principle of least energy
View Answer
Explanation: Governing equations of displacement-based plate theories are derived using the principle of virtual displacements, the principle of virtual displacements directly yields the weak forms of the governing equations. The starting point in the development of the governing equations of a plate theory is to choose a displacement field. Typically, the displacement components are selected in the form of a linear combination of unknown functions and powers of the thickness coordinate z so that certain kinematics (i.e., the geometry of deformation) of the plate are represented.
5. In FEM, which theory is an extension of the Euler-Bernoulli beam theory?
a) Classical Plate Theory
b) Shear Deformation Theory
c) Hencky-Mindlin plate theory
d) Shell theory
View Answer
Explanation: The two most commonly used displacement-based plate theories are the Classical Plate Theory (CPT) and first-order Shear Deformation Theory (SDT). CPT is an extension of the Euler-Bernoulli beam theory from one dimension to two dimensions and is also known as the Kirchhoff plate theory. Shear Deformation Theory is an extension of the Timoshenko beam theory.
6. In displacement-based plate theories, which option is not an assumption of Classical Plate Theory (CPT)?
a) A straight line perpendicular to the plane of the plate is inextensible
b) A straight line perpendicular to the plane of the plate remains straight
c) A straight line perpendicular to the plane of the plate remains straight and does not rotate
d) A straight line perpendicular to the plane of the plate rotates such that it remains perpendicular to the tangent to the deformed surface
View Answer
Explanation: The Classical Plate Theory is based on the assumption that a straight line perpendicular to the plane of the plate is (1) inextensible, (2) remains straight, and (3) rotates such that it remains perpendicular to the tangent to the deformed surface. These assumptions are also specified as εzz=0, εyz=0, εxz=0 for a plate in XY plane.
7. Which option specifiesan assumption made in Classical Plate Theory for a plate lying in the plane XY?
a) εzz=0
b) εxz≠0
c) εyz≠0
d) εxy=0
View Answer
Explanation: The assumption made in Classical Plate Theory is that a straight line perpendicular to the plane of the plate is (i) inextensible, (ii) remains straight, and (iii) rotates such that it remains perpendicular to the tangent to the deformed surface. These assumptions are equivalent to specifying εzz=0, εyz=0, εxz=0 for a plate in XY plane.
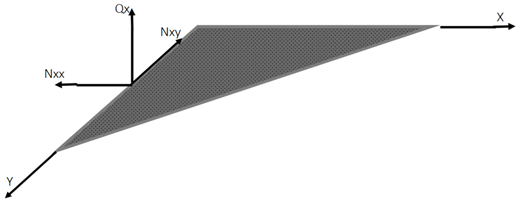
8. The following diagram is the mid-plane of an elastic plate. Which option shows the correct moments Mxx and Mxy if the plate is loaded as per the Classical Plate Theory?
a) 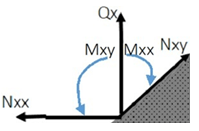
b) 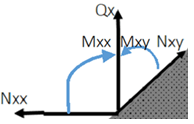
c) 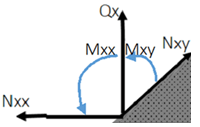
d) 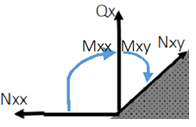
View Answer
Explanation: The given diagram shows bending moment and shear force in a plate lying in XY plane. The term Q is concentrated transverse load, N is shear force, and Mxx is edge bending moment whereas Mxy is the twisting moment. The option ‘a’ is correct for the sense of the moments but not for their positions.
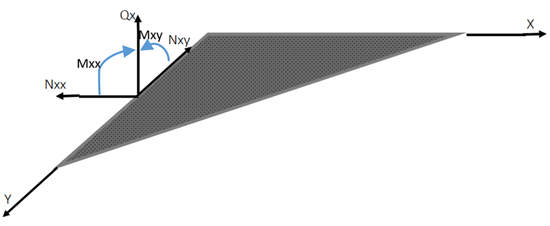
9. The following figure shows the mid-plane of an elastic plate. What are the boundary conditions in Classical Plate Theory if the plate is clamped and the displacement along Z is w?
a) w=0,\(\frac{\partial w}{\partial n}\)=0
b) w=0,Vn=0
c) w=0,\(\frac{\partial w}{\partial n}\)≠0
d) w=0,Mnn=0
View Answer
Explanation: Geometrically, plate problems are similar to the plane stress problems except that plates are also subjected to transverse loads that cause bending about axes in the plane of the plate. The boundary condition for a clamped plate is the absence of deflection and normal derivative of deflection (slope), i.e., w=\(\frac{\partial w}{\partial n}\)=0. Because a simply supported end does not restrict rotation, the reactive moment is zero, i.e., w=Mnn=0. For a free end, both, the reactive moment and the shear force are absent, i.e., Mnn= Vn=0.
10. The following figure shows the mid-plane of an elastic plate. In Classical Plate Theory, what are the boundary conditions ifthe plate is simply supported with deflection w along Z?

a) w=0,\(\frac{\partial w}{\partial n}=0\)
b) w=0,Vn=0
c) w=0,\(\frac{\partial w}{\partial n}\)≠0
d) w=0,Mnn=0
View Answer
Explanation: Plate problems are geometrically similar to the plane stress problems except that plates are also subjected to transverse loads. A clamped plate has no deflection and normal derivative of deflection (slope), i.e., w=\(\frac{\partial w}{\partial n}\)=0. In a simply supported end, rotation is not restricted; thus, the reactive moment is zero, i.e., w= Mnn=0. A free end has no reactive moment and the shear force, i.e., Mnn= Vn=0.
11. In FEM, what are the primary variables in the Classical Plate Theory of plate deformation (w)?
a) The transverse deflection w only
b) The transverse deflection w and the normal derivative of w
c) The normal derivative of w only
d) The normal and the time derivative of w
View Answer
Explanation: An examination of the boundary terms in the weak form of Classical Plate Theory suggests that the essential boundary conditions involve specifying the transverse deflection w and the normal derivative of w, which constitute the primary variables of the problem (like in the Euler-Bernoulli beam model). Hence, the finite element interpolation of w must be such that w and \(\frac{dw}{dn}\) are continuous across the inter-element boundaries in CPT elements.
12.How many termpolynomial is used in the approximation of w for a three noded triangular element with three DOF at each node?
a) 9-term
b) 18-term
c) 6-term
d) 12-term
View Answer
Explanation: Several C1 rectangular and triangular plate bending elements with (w, \(\frac{dw}{dx}\),\(\frac{dw}{dy}\)) or with (w,\(\frac{dw}{dx}\),\(\frac{dw}{dy}\),\(\frac{d^2w}{dy^2}\)) as the degrees of freedom at each node exists in the literature. A triangular element with three nodes, with (w, \(\frac{dw}{dx}\),\(\frac{dw}{dy}\))at each node, requires the 9-term (n=9) polynomial approximation of w, i.e.,w=a1+a2x+a3y+a4xy+a5x2+a6y2+a7(x2y+xy2)+a8x3+a9y3.
13. In Classical Plate Theory, what is the correct comment for the polynomial w=a1+a2x+a3y+a4xy+a5x2+a6y2+a7(x2y+xy2)+a8x3+a9y3?
a) It is used in the approximation of deflection for a rectangular element
b) It is a complete third order polynomial
c) It’s an incomplete third order polynomial
d) w varies as a quadratic along any line x=constant
View Answer
Explanation: Several C1 rectangular and triangular plate bending elements with (w, \(\frac{dw}{dx}\),\(\frac{dw}{dy}\)) or with (w,\(\frac{dw}{dx}\),\(\frac{dw}{dy}\),\(\frac{d^2w}{dy^2}\)) as the degrees of freedom at each node exists in the literature. A triangular element with three nodes, with (w, \(\frac{dw}{dx}\),\(\frac{dw}{dy}\)) at each node, requires the 9-term (n=9) polynomial approximation of w, i.e., w=a1+a2x+a3y+a4xy+a5x2+a6y2+a7(x2y+xy2)+a8x3+a9y3. This is an incomplete third-order polynomial because x2y and y2x do not vary independently. We note from the equation that w varies as a cubic along with any line x=constant or y=constant.
14. In Classical Plate Theory, because the 4-noded rectangular element is non-conforming, it gives poor results in approximation.
a) True
b) False
View Answer
Explanation: Elements that violate any of the continuity conditions are known as non-conforming elements. Thus, the four-node rectangular element with w approximated by a 12-term polynomial is non-conforming. Despite this deficiency, the element is known to give good results. A similar discussion leads to the conclusion that the three-node triangular element is the non-conforming type and found to have convergence problems and singular behavior for certain meshes.
15. In Classical Plate Theory, how many triangles assemble to give a conforming triangular element with DOF w, \(\frac{dw}{dy}\) and \(\frac{dw}{dy}\) at each vertex?
a) 1
b) 3
c) 4
d) 12
View Answer
Explanation: A non-conforming element is the one that violates any of the continuity conditions. The three-node triangular element is non-conforming and found to have convergence problems and singular behavior for certain meshes. A conforming triangular element (due to Clough and Tocher) is an assemblage of three triangles. The interpolation functions for the triangular element can be expressed in terms of the area coordinates. A confirming rectangular element is formed as an assembly of twelve triangular elements.
Sanfoundry Global Education & Learning Series – Finite Element Method.
To practice all areas of Finite Element Method, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Check Civil Engineering Books
- Check Mechanical Engineering Books
- Practice Civil Engineering MCQs
- Practice Mechanical Engineering MCQs
- Check Finite Element Method Books
