This set of Finite Element Method Assessment Questions and Answers focuses on “Penalty – Finite Element Model – 2”.
1. Which option is correct regarding constraints in the viscous flow problems governed by the continuity and momentum equation?
a) Constrains are readily available
b) Constraints are created by the elimination of pressure
c) Constraints are created by the elimination of velocity
d) No constraints are dealt with in penalty formulation
View Answer
Explanation: In viscous flow problems, constrains are not readily available from the presented equations. Since pressure is not present in all the governing equations, we eliminate it from the given other equations. The constraints are created on velocity by the elimination of pressure, and thus, the penalty method is applied.
2. In the finite element method, which option is not a natural and direct formulation of momentum and continuity equations?
a) Velocity-pressure formulation
b) Penalty formulation
c) Mixed formulation
d) Lagrange multiplier formulation
View Answer
Explanation: There are two different finite element models of momentum and continuity equations. The first one is a natural and direct formulation of momentum and continuity equations. It is known as the velocity-pressure formulation or mixed formulation. Lagrange multiplier formulation is similar to the velocity-pressure formulation. The penalty formulation is not natural and direct.
3. For the functional Iv(v)=\(\frac{1}{2}\)Bv(v,v)-l(v), which option is equivalent to the equations governing steady flows of viscous incompressible fluids?
a) Minimize lv
b) Maximize lv
c) Stationary lv
d) Derivative of lv
View Answer
Explanation: For the quadratic functional given by the equation Iv(v)=\(\frac{1}{2}\)Bv(v,v)-l(v), one can state that the equations governing steady flows of viscous incompressible fluids are equivalent to minimize Iv(v), subject to the constraint \(\frac{\partial v_x}{\partial x}+\frac{\partial v_y}{\partial y}\)=0. It is a constrained problem of finding velocity.
4. In FEM, what is the characteristic of the problem with the functional Iv(v) representing governing equations of steady viscous incompressible flows?
a) It is subjected to constraint \(\frac{\partial v_x}{\partial x}+\frac{\partial v_y}{\partial y}\)=0
b) It is an unconstrained problem
c) It can be reformulated as a constrained one, by using the penalty method
d) It cannot be reformulated as an unconstrained one, by using the penalty method
View Answer
Explanation: For the functional Iv(v), one can state that the equations governing steady flows of viscous incompressible fluids are equivalent to minimize Iv(v), subject to the constraint \(\frac{\partial v_x}{\partial x}+\frac{\partial v_y}{\partial y}\)=0. It is a constrained problem that can be reformulated as an unconstrained one by using the penalty method.
5. In the Lagrange multiplier method, a constrained problem is reformulated as one of finding the stationary points of an unconstrained function, whereas in the penalty method, a problem with differential constraints is reformulated to one without constraints.
a) True
b) False
View Answer
Explanation: In the Lagrange multiplier method, a constrained problem is reformulated as one of finding the stationary points of the unconstrained functional IL(v,λ)≡Iv(v)+∫ΩcλG(v)dxdy where λ(x,y) is the Lagrange multiplier. In the penalty method, a problem with differential constraints is reformulated to one without constraints.
6. For the functional IL(v,λ)≡Iv(v)+∫ΩcλG(v)dxdy, what is the necessary condition for IL to have a stationary value?
a) δvxIL+δvyIL+δλIL=0
b) δvxIL-δvyIL-δλIL=0
c) δvxIL-δvyIL+δλIL=0
d) δvxIL+δvyIL-δλIL=0
View Answer
Explanation: In the Lagrange multiplier method the constrained problem is reformulated as one of finding the stationary points of the unconstrained functional IL(v,λ)≡Iv(v)+∫ΩcλG(v)dxdy where λ(x,y) is the Lagrange multiplier. The necessary condition for IL to have stationary value is δvxIL+δvyIL+δλIL=0.
7. In FEM, which option is a negative aspect of the mixed formulation?
a) Presence of zeros on matrix diagonals corresponding to pressure variable
b) Involves a natural and direct formulation
c) It is a velocity-pressure formulation
d) It is similar to the Lagrange multiplier method
View Answer
Explanation: A negative aspect of the mixed finite element model is the presence of zeroes on the matrix diagonals corresponding to the pressure variables. Direct equation-solving methods must use some type of pivoting strategy, while the use of iterative solvers is severely handicapped by poor convergence behavior.
8. In the computation of mixed formulation in FEM, which option is correct for the nodal DOF of the following element?
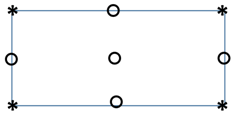
a) o nodes with u,v and P
b) * nodes with u,v and P
c) o nodes with P only
d) *nodes with u and v
View Answer
Explanation: Commonly used elements for two-dimensional flows of viscous incompressible fluids are the triangular and quadrilateral elements. In the case of linear elements, the pressure is treated as discontinuous between elements. In quadratic elements, the DOF at intermediate and interior nodes is velocity, i.e., u and v, whereas DOF at corner nodes are u, v and P.
9. For the following slider bearing, the upper pad is inclined to the base pad. Which option is correct for a load applied normal to the base pad?
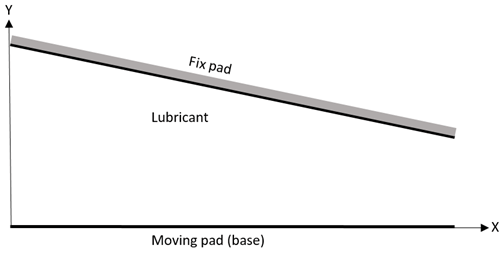
a) A pressure gradient develops in the lubricant, and the bearing can support some transverse load
b) The pressure remains uniform in the lubricant, and the bearing can support some transverse load
c) A pressure gradient develops in the lubricant, and the bearing cannot support any transverse load
d) The pressure remains uniform in the lubricant, and the bearing cannot support any transverse load
View Answer
Explanation: The slider (or slipper) bearing consists of a short sliding pad over a stationary pad, and the small gap between the two pads is filled with a lubricant. If the upper pad is inclined to the base plate, then a pressure gradient develops in the lubricant, and the bearing can support some transverse load. The penalty formulation in FEM is used to solve for pressure and velocities of flow.
10. For the following slider bearing, the upper pad is parallel to the base pad. Which option is correct for a load applied normal to the base pad?
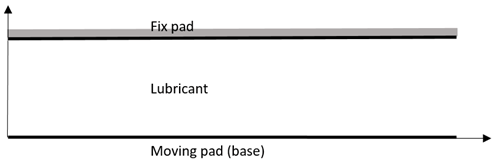
a) The pressure in the lubricant is atmospheric, and the bearing cannot support any load
b) The pressure in the lubricant is greater than atmospheric, and the bearing can support any load
c) The pressure in the lubricant is less than atmospheric, and the bearing cannot support any load
d) The pressure in the lubricant is atmospheric, and the bearing can support some load
View Answer
Explanation: The slider (or slipper) bearing consists of a short sliding pad over a stationary pad, and the small gap between the two pads is filled with a lubricant. If the upper pad is parallel to the base plate, then the pressure everywhere in the gap is atmospheric (because dP/dx is a constant for flow between parallel plates), and the bearing cannot support any transverse load. The penalty formulation in FEM is used to solve for pressure and velocities of flow.
Sanfoundry Global Education & Learning Series – Finite Element Method.
To practice all areas of Finite Element Method Assessment Questions, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Practice Civil Engineering MCQs
- Practice Mechanical Engineering MCQs
- Check Civil Engineering Books
- Apply for Civil Engineering Internship
- Check Finite Element Method Books
