This set of Finite Element Method Multiple Choice Questions & Answers (MCQs) focuses on “Plane Elasticity – Weak Formulations”.
1. In FEM, which method is not used to construct the weak forms and associated finite element model of the plane elasticity equations?
a) Principle of virtual displacements
b) The principle of minimum total potential energy
c) Weak form of governing differential equations
d) Hamiltonian principle
View Answer
Explanation: There are two different ways of constructing the weak forms and associated finite element model of the plane elasticity equations. The first one uses the principle of virtual displacements (or the principle of minimum total potential energy), while the second approach follows a three-step procedure to obtain a weak form of governing differential equations.
2. In constructing the weak forms of plane elasticity problems, which option is not related to the principle of virtual displacements?
a) Displacements to strains
b) Strains to stresses
c) The equations of motion
d) Body forces
View Answer
Explanation: Among the ways of constructing the weak forms and associated finite element model of the plane elasticity equations, the principle of virtual displacements (or the principle of minimum total potential energy) is expressed in terms of matrices relating displacements to strains, strains to stresses, and the equations of motion. This approach is used in most finite element texts on solid mechanics.
3. What is the correct form of the principle of virtual displacements applied to plane finite elastic element If Ve is the volume of element and se is its surface?
a) 0=\(\int_{V_e}\)(σijδεij+ρüiδui)dV-\(\int_{V_e}\)fiδuidV-∮se\(\hat{t_i}\)δuids
b) 0=\(\int_{V_e}\)(σijδεij+ρu̇iδui)dV-\(\int_{V_e}\)fiδuidV-∮se \(\hat{t_i}\)δuids
c) 0=\(\int_{V_e}\)(σijδεij+ρüiδui)dV+\(\int_{V_e}\)fiδuidV-∮se \(\hat{t_i}\)δuids
d) 0=\(\int_{V_e}\)(σijδεij+ρu̇iδui)dV\(\int_{V_e}\)fiδuidV+∮se \(\hat{t_i}\)δuids
View Answer
Explanation:The vector form of the principle of virtual displacements applied to plane finite elastic element with volume, Ve and surface, se is 0=\(\int_{V_e}\)(σijδεij+ρüiδui)dV-\(\int_{V_e}\)fiδuidV-∮se\(\hat{t_i}\) δuids, where “δ” denotes the variational operator, (σij and εij are the components of stress and strain tensors, respectively, and fi and ti are the components of the body force and boundary stress vectors, respectively.
4. In the weak formulation of the plane elasticity equations, even though the methods, the principle of virtual displacements and the three-step weak formulation, give, mathematically different finite element models, they are the same in their algebraic forms.
a) True
b) False
View Answer
Explanation: There are two different ways of constructing the weak forms and associated finite element model of the plane elasticity equations. The first one is the principle of virtual displacements, while the second is a three-step procedure to obtain a weak form of governing differential equations. Of course, both methods give, mathematically, the same finite element model, but differ in their algebraic forms.
5. In the weak form of the principle of virtual displacements, 0=\(\int_{V_e}\)(σijδεij+ρüiδui)dV-\(\int_{V_e}\)fiδuidV-∮set̂iδuids , applied to plane finite elastic element,which term corresponds to virtual strain energy stored in the body?
a) \(\int_{V_e}\)(σijδεij)dV
b) ∮set̂ iδuids
c) \(\int_{V_e}\)(ρü iδui)dV
d) \(\int_{V_e}\)fiδuidV
View Answer
Explanation: There are four terms in the vector form of the principle of virtual displacements applied to plane finite elastic element, 0=\(\int_{V_e}\)(σijδεij+ρüiδui)dV-\(\int_{V_e}\)fiδuidV-∮set̂iδuids. The first term in the equation corresponds to the virtual strain energy stored in the body.The second term deals with the kinetic energy stored in the body; the third term represents the virtual work done by the body force, and the fourth term represents the virtual work done by the surface traction.
6. In the weak form of the principle of virtual displacements applied to a plane elastic finite element, what does the term \(\int_{V_e}\)(ρü iδui)dV correspond to?
a) Virtual strain energy
b) Kinetic energy
c) Virtual work done by the body force
d) Virtual work done by the surface traction
View Answer
Explanation: Thefour terms in the vector form of the principle of virtual displacements are present in the equation, 0=\(\int_{V_e}\)(σijδεij+ρüiδui)dV-\(\int_{V_e}\)fiδuidV-∮set̂iδuids. The given term corresponds to the kinetic energy stored in the body, the third term represents the virtual work done by the body force, and the fourth term represents the virtual work done by the surface traction.
7. Under plane elasticity, which force is responsible for doing the virtual work \(\int_{V_e}\)fiδuidV in the weak form of the principle of virtual displacements?
a) Body force
b) Concentrated loads
c) Surface traction force
d) Pressure force
View Answer
Explanation:Of the four terms present in the vector form of the principle of virtual displacements applied to plane finite elastic element, 0=\(\int_{V_e}\)(σijδεij+ρüiδui)dV-\(\int_{V_e}\)fiδuidV-∮set̂iδuids, the first term one corresponds to the virtual strain energy stored in the body. The second term corresponds to the kinetic energy stored in the body. The given term is the third term in the equation, and that represents the virtual work done by the body force.
8. For a plane elasticity problem, which term in the weak form of the principle of virtual displacements is affected by a change in the applied surface traction forces?
a) \(\int_{V_e}\)(σijδεij)dV
b) ∮set̂ iδuids
c) \(\int_{V_e}\)(ρü iδui)dV
d) \(\int_{V_e}\)fiδuidV
View Answer
Explanation:The vector form of the principle of virtual displacements applied to the plane finite elastic element consists of four terms. Two terms correspond to energy stored in the body. The term, ∮set̂ iδuids represents the virtual work done by the surface traction forces, and thus, it is affected by a change in the applied surface traction forces.
9. If U,V denotes the components of the displacement vector, then which option is the correct primary nodal degrees of freedom present in the following figure of a plane elasticity problem?
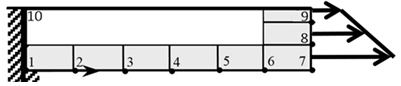
a) U1=V1=0
b) U2≠0, V2=0
c) U2=0, V2≠0
d) U1=V1≠0
View Answer
Explanation: A fixed connection implies that all components of displacement are zero, whereas roller support indicates that the displacement normal to the wall is zero. In the given problem, U and V denote the horizontal and vertical displacements, respectively, at the global ith node of the mesh. The specified primary degrees of freedom (i.e., displacements) include U1=V1= U10=V10=0, U2≠0 and V2≠0.
10. If Fx, Fy denotes the components of the force vector, then which option is the correct secondary degrees of freedom present in the following figure of a plane elasticity problem?

a) \(F_6^x=F_6^y\)≠0
b) \(F_7^x=F_7^y\)≠0
c) \(F_6^x\ne F_6^y\)=0
d) \(F_7^x\ne F_7^y\)=0
View Answer
Explanation: The procedure to calculate the nodal forces is the same as that used for the calculation of nodal sources single-variable problems, except that the nodal values must be decomposed into the x and y components. Since the distributed force is along the x coordinate, all nodal computed nodal forces are along the x coordinate. The specified secondary degrees of freedom (i.e., forces) include \(F_6^x=F_6^y=F_7^y=0\) But
\(F_7^x\)≠0.
11. For plane elasticity problems, which option represents the essential boundary conditions among the governing equations?
a) Displacements, ux and uy at the boundary
b) Surface traction at the boundary
c) The displacements (ux and uy) and surface traction at the boundary
d) Stresses in the element
View Answer
Explanation: For plane elasticity problems, the boundary conditions are one of the governing equations. There are two types of boundary conditions, namely, essential boundary conditions and natural boundary conditions. The displacements specified in the problem are the essential boundary condition or Dirichlet boundary condition.
12. If the equation ∫Ωche\((\frac{\partial w_1}{\partial x}\sigma_{xx}+\frac{\partial w_1}{\partial y}\)σxy-w1fx+ρw1\(\ddot{u_x})\)dxdy-∮Γchew1(σxxnx+σxyny)ds=0 represents the weak form of plane elasticity equations, then the weight functions w1 and w2 are the first variations of ux and uy, respectively.
a) True
b) False
View Answer
Explanation: The equations ∫Ωche\((\frac{\partial w_1}{\partial x}\sigma_{xx}+\frac{\partial w_1}{\partial y}\)σxy-w1fx+ρw1\(\ddot{u_x})\)dxdy-∮Γchew1(σxxnx+σxyny)ds=0 and ∫Ωche\((\frac{\partial w_2}{\partial x}\sigma_{xy}+\frac{\partial w_2}{\partial y}\)σyy-w2fy+ρw2\(\ddot{u_y})\)dxdy-∮Γchew2(σxynx+σyyny)ds=0 represents the weak forms of plane elasticity equations, where Ω is the area of cross-section of the domain, ┌ is a portion of element boundary, and the weight functions w1 and w2 are the first variations of ux and uy respectively.
Sanfoundry Global Education & Learning Series – Finite Element Method.
To practice all areas of Finite Element Method, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Check Finite Element Method Books
- Apply for Civil Engineering Internship
- Apply for Mechanical Engineering Internship
- Practice Mechanical Engineering MCQs
- Practice Civil Engineering MCQs
