This set of Finite Element Method Multiple Choice Questions & Answers (MCQs) focuses on “Library of Elements and Interpolation Functions – 1”.
1. Which option is not correct about the three-noded triangular plane stress (linear) element used in FEM?
a) It has six degrees of freedom
b) It belongs to both the isoparametric and superparametric element families
c) It can be improved by the addition of internal degrees of freedom
d) Delaunay triangulation can be used for its mesh generation
View Answer
Explanation: The three-node triangular element with linear displacements for the plane stress problem is simply called a linear triangle. It has six degrees of freedom and it belongs to both the isoparametric and superparametric element families. A mesh of linear trianglecan be easily generated using Delaunay triangulation, but the element cannot be improved by the addition of internal degrees of freedom; rather, it can be improved by increasing the number of nodes.
2. In FEM, which option is used to develop the Higher-order triangular elements (i.e. triangular elements with interpolation functions of higher degree) systematically?
a) Pascal’s triangle
b) Galerkin method
c) Jacobi method
d) Delaunaytriangulation
View Answer
Explanation: The Higher-order triangular elements (also the Lagrange family of triangular elements) can be systematically developed with the help of Pascal’s triangle. Finite element equations are obtained using the Galerkin method. Jacobi is used for eigenvalue problems. The Delaunay method is used to generate mesh for triangular elements.
3. In FEM, What is the number of displacement polynomials necessary for finding displacements in a linear triangular element?
a) 1
b) 2
c) 3
d) 4
View Answer
Explanation: The number of displacement polynomials for an element is equal to the degrees of freedom of each node of the element. A linear triangular element has three nodes and two degrees of freedom at each node. Thus, the total number of displacement polynomials necessary for finding displacements is two.
4. Concerning triangular elements in FEM, which option is not correct about the mathematical formula of Pascal’s triangle?
a) It contains the terms in two coordinates only
b) The position of the terms can be viewed as the nodes of a triangular element
c) The position of the first and last terms of a row is at the vertices of a triangular element
d) A triangular element of order 2 corresponds to the second row
View Answer
Explanation: A Pascal’s triangle contains the terms of polynomials of various degrees in two coordinates. We can view the positions of the terms as nodes of a triangular element, with the constant term and the first and last terms of a given row being the vertices of the triangle. A triangular element of order 2 (i.e., the degree of the polynomial is 2) contains six nodes and corresponds to the third row of Pascal’s triangle.
5. Which option is not correct about the four-noded rectangular plane stress element used in FEM?
a) It has eight degrees of freedom
b) Shape functions N1, N2, N3 and N4 are bilinear functions of x and y
c) The displacement field is continuous across elements
d) Its Delaunay triangulation is unique
View Answer
Explanation: The four-node quadrilateral element with linear displacements for a plane stress problem has two degrees of freedom at each node. The total degrees of freedom of the element is eight. The displacement field is continuous across elements connected at nodes and the shape functions N1, N2, N3 and N4 are bilinear functions of x and y. Its Delaunay triangulationis not unique, but it has two solutions.
6. In FEM, if x, y represents Cartesian coordinates, then the following triangular array of binomial coefficients forms Pascal’s triangle.
\(\begin{matrix}
& & & 1 & & &\\
& & x & & y & & \\
& x^2 & & xy & & y^2 & \\
x^3 & & x^2y & & xy^2 & & y^3 \\
\end{matrix}
\)
a) True
b) False
View Answer
Explanation: In mathematics, Pascal’s triangle is a triangular array of binomial coefficients. It contains the terms of polynomials of various degrees in two coordinates x and y. An nth row of Pascal’s triangle contains n term(s), and it corresponds to all triangular elements with at least 0.5n(n+1) number of nodes. The 1st row contains number one only.
7. In the FEM element library, what is the other name of a higher-order element?
a) Complex element
b) Simplex element
c) Linear element
d) Nonlinear element
View Answer
Explanation: Simplex and linear elements contain nodes only at endpoints but not at the interior. They have linear polynomials as interpolation functions. Higher-order elements can be created easily from simplex elements by adding additional intermediate nodes to each element. They are also called complex elements.
8. In FEM, if x, y represents Cartesian coordinates, then which term of Pascal’s triangle corresponds to the position of the interior node of the following element?
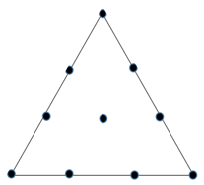
a) 1
b) xy
c) x2y
d) xy2
View Answer
Explanation: The interior node of the ten noded triangular elements can be viewed as the middle term of the third row of Pascal’s triangle. Since the 3rd row contains three terms viz. x2, xy and y2 in the same order, the interior node corresponds to the term xy. An nth row of Pascal’s triangle contains n term(s) and it corresponds to all triangular elements with at least 0.5n(n+1) number of nodes.
9. In the FEM element library, an eight noded quadrilateral element belongs to which family?
a) Serendipity
b) Linear
c) Simplex
d) Quadratic
View Answer
Explanation: The Serendipity elements are the rectangular elements with intermediate nodes but no interior nodes, i.e., all nodes lie on boundary. Since four nodes of an eight noded quadrilateral element are intermediate nodes, it belongs to the Serendipity family. Simplex and linear elements contain nodes only at endpoints but not at intermediate points. They have linear polynomials as interpolation functions. A quadratic element contains interior nodes.
10. In FEM, which option is not correct about the Lagrange family of triangular elements?
a) The nodes are uniformly spaced
b) Pascal’s triangle can be viewed as a triangular element
c) Dependent variables and their derivatives are continuous at inter-element boundaries
d) 2nddegree polynomial corresponds to 6 noded triangle
View Answer
Explanation: In Lagrange family elements the nodes are regularly placed everywhere on the grid i.e., they are uniformly spaced. The location of the terms in Pascal’s triangle gives the location of nodes in elements. Thus, Pascal’s triangle can be viewed as a triangular element. The derivatives of dependent variables are not continuous at inter-element boundaries. 2nd-degree polynomial corresponds to 6 noded triangles.
11. What is the displacement function for one-dimensional, two noded linear elements in terms of its shape functions N1 and N2?
a) N1u1+N2u2
b) N1u2+N2u1
c) N1u1-N2u2
d) N1u2-N2u1
View Answer
Explanation: For a linear element, the displacement function is a linear polynomial of nodal displacements. A one-dimensional, two noded linear elements have two nodes with corresponding displacements u1, u2 and corresponding shape functions N1, N2. The displacement function is given by N1u1+N2u2.
12. For the following element, what is the value of the distance variable s at the 1st row?
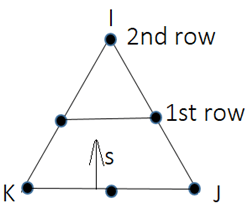
a) 1
b) 2
c) 0.5
d) 0
View Answer
Explanation: The value of the distance variable s is \(\frac{p}{k-1}\); where p is the row at which s is calculated, k is the number of uniformly spaced nodes per side of the element. For a quadratic element, we have k = 3.
s=\(\frac{p}{3-1}\)
=\(\frac{p}{2}\)
At first row, p=1
s=\(\frac{1}{2}\)
=0.5.
13. For the following element, if s is the distance variable as shown, then its value at the 2nd row is \(\frac{1}{3}\).
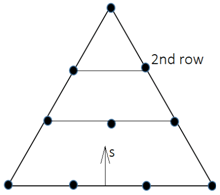
a) True
b) False
View Answer
Explanation: The value of the distance variables s is \(\frac{p}{k-1}\); where p is the row at which s is calculated, k is the number of uniformly spaced nodes per side of the element. For a given element, we have k = 4.
s=\(\frac{p}{4-1}\)
=\(\frac{p}{3}\)
At second row, p=2
s=\(\frac{2}{3}\).
14. In the FEM element library, what is the correct name for a six noded triangular element?
a) Linear strain triangular element
b) Constant strain triangular element
c) Variable strain triangular element
d) Higher-order triangular element
View Answer
Explanation: A Constant strain triangular (CST) element is the simplest triangular element with three end nodes. A Linear strain triangular element (LST) is a six-noded triangular element with three intermediate nodes in addition to three end nodes. For plane stress applications, LST gives an accurate result compare to the three-noded CST element. The variable strain triangular element is a higher-order triangular element with more than six nodes.
To practice all areas of Finite Element Method, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Check Mechanical Engineering Books
- Practice Civil Engineering MCQs
- Apply for Mechanical Engineering Internship
- Apply for Civil Engineering Internship
- Check Civil Engineering Books
