This set of Finite Element Method Multiple Choice Questions & Answers (MCQs) focuses on “Beams with Combine Loads”.
1. What type of loading is depicted in the figure given below?
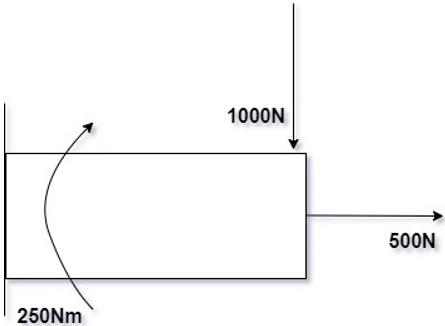
a) Axial Load only
b) Bending Load only
c) Combined Loading
d) Torsion Load only
View Answer
Explanation: Combined type of loading is depicted in the figure. It clearly shows the application of more than one type of loading. In the given figure the beam member is under the application of 3 different types of loading. They are Axial load = 500N, Bending load = 1000N, and Torque = 250Nm.
2. When is a beam said to be under the application of Combined Loading?
a) When it is being acted upon by one type of load only
b) When it is under the influence of two types of loading
c) There is no such concept of combined loading
d) When it is under the influence of one or more types of loading
View Answer
Explanation: A beam is said to be under the application of combined loading when it is under the influence of one or more types of loading. There is no restriction as to the number and types of loads applicable for the same. A beam member under the influence of two different types of loading is also said to be acted upon by combined loading.
3. When a beam is under the application of combined loading, the total stress is equal to the product of the individual stresses.
a) True
b) False
View Answer
Explanation: When a beam is under the application of combined loading, the total stress is equal to the summation of the individual stresses. For instance, if a beam is under the influence of Axial and Bending loads; then the total stress = Axial stress + Bending stress.
4. In combined loading, if stresses are acting in multiple directions they are added together only if they are pointing in the same direction.
a) True
b) False
View Answer
Explanation: When an object is experiencing stresses in multiple directions, the rule of vector addition is used. Stresses acting in the same direction are added, while those acting in opposite directions are subtracted.
5. What is the expression for resultant stress of a beam acting under the combined influence of Axial and Bending load? Given: Load = P N, Area = Amm2, Bending Moment = M Nm, Moment of inertia = I mm4, Vertical distance from neutral axis = y mm.
a) (P / A) * (My / I)
b) (P / A) + (My / I)
c) (P / A) – (My / I)
d) (P / A) / (My / I)
View Answer
Explanation: The expression for resultant stress of a beam acting under the combined influence of Axial and Bending load is given by (P / A) – ((My) / I); where P = load acting, A = Cross sectional area of the beam, M = Bending Moment, y = vertical distance from the neutral axis, and I = Moment of Inertia.
6. What is the resultant stress of a beam acting under the combined influence of Axial and Bending load? Given: Axial Load (P) = 100N, Bending Moment (M) = 150Nm, Moment of Inertia (I) = 1000mm4, Vertical distance from neutral axis (y) = 15mm, Area of cross section of beam = 400mm2.
a) – 14.75N / mm2
b) 146.8N / mm2
c) 14.75N / mm2
d) 140.83N / mm2
View Answer
Explanation: Load (P) = 100N, Bending Moment (M) = 150Nm, Moment of Inertia (I) = 1000mm4, Vertical distance from neutral axis (y) = 15mm, Area of cross section of beam = 400mm2
We know that resultant stress = (P / A) – (My / I)
= (100 / 400) – ((150 * 15) / 1000)
= – 14.75N / mm2
7. If a beam is subjected to axial, bending and Torsional loads; only the axial and bending loads can be added together. Why is this so?
a) Because the axial and bending loads are acting in the same direction
b) Torsional load is minimal
c) Axial and bending loads are normal loads
d) Axial and bending loads give rise to shear stresses
View Answer
Explanation: When a beam is under the application of combined loading, the resultant total stress is equal to the summation of the individual stresses. However, it is an implied condition that only the normal stresses can be added together; and shear stresses can be added together. In this case, axial and bending loads fall under the Normal stresses, whereas the Torsional load is that of a shear stress.
8. Which of the following defines a normal stress component that arises due to the application of combined loading?
a) Stress due to load applied perpendicular to it
b) Stress due to load applied parallel to it
c) Stress due to Torsion
d) Stress due to bending
View Answer
Explanation: Normal stress is the result of load application perpendicular to the member. For instance, Axial and Bending loads give rise to normal stress components as their application is perpendicular to the member under discussion.
9. Which of the following defines a shear stress component that arises due to the application of combined loading?
a) Stress due to Combined loading
b) Stress due to load applied parallel to it
c) Stress due to Axial Loading
d) Stress due to Compressive Loading
View Answer
Explanation: Shear stress is the result of load application parallel to the member. For instance, Torsion and Bending loads give rise to normal stress components as their application is parallel to the member under discussion.
10. What is the axial load acting on a beam if the resultant stress is given as 0.541N / mm2? Given – Resultant stress = 0.541N / mm2, Bending Moment (M) = 450Nm, Moment of Inertia (I) = 2000mm4, Vertical distance from neutral axis (y) = 5mm, Area of cross section of beam = 600mm2.
a) 9000N
b) 99.96N
c) 999.6N
d) 943N
View Answer
Explanation: Resultant stress = 0.541N / mm2, Bending Moment (M) = 450Nm, Moment of Inertia (I) = 2000mm4, Vertical distance from neutral axis (y) = 5mm, Area of cross section of beam = 600mm2
We know that resultant stress = (P / A) – (My / I)
0.541 = (P / 600) – ((450 * 5) / 2000)
.541 + ((450 * 5) / 2000) = P / 600
1.666 * 600 = P
P = 999.6 N
Sanfoundry Global Education & Learning Series – Finite Element Method.
To practice all areas of Finite Element Method, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Practice Civil Engineering MCQs
- Check Civil Engineering Books
- Apply for Civil Engineering Internship
- Practice Mechanical Engineering MCQs
- Check Mechanical Engineering Books
