This set of Finite Element Method Multiple Choice Questions & Answers (MCQs) focuses on “Boundary Value Problems – 1”.
1. In Finite Element Methods (FEM), in two-dimensional problems, we approximate solution on a domain but not the domain itself.
a) True
b) False
View Answer
Explanation: In two-dimensional problems, the finite elements are simple geometric shapes. These shapes can be used to approximate a given domain as well as the solution over it. Because of double approximation the accuracy of solution depends on both the approximations and is errors in two approximations gets multiplied.
2. In Finite Element Methods (FEM), a boundary value problem is a set of differential equations with a solution, which also satisfies some additional constraints, known as ___
a) boundary conditions
b) nodal values
c) equilibrium equations
d) energy minimum
View Answer
Explanation: A boundary value problem is a set of differential equation with a solution, which also satisfies some additional constraints, called the boundary conditions. Nodal Values are the values of a variable at each node obtained as a result of finite element analysis. Equilibrium equations are used in free body diagrams.
3. Which of the following expression is the correct solution (u) for finite element approximation over the 3 noded element shown?
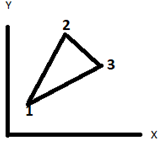
a) u=c1+x*c2+y*c3
b) u=c1+x*c2+y*c1
c) u=c1+x*c2+y*c3+x*y
d) u=x*c1+y*c2
View Answer
Explanation: The polynomial u=c1+x*c2+y*c3 is the correct solution (u) for finite element approximations over the 3 noded element. It satisfies the conditions in order for the approximate solution to be convergent to the true solution. Here c1, c2 and c3 are shape functions and the set of coefficients {1,x,y} is continuous, linearly independent and complete.
4. For A1, A2, and A3 as area coordinates and s1, s2 and s3 as shape functions for the element shown, which relation is correct?
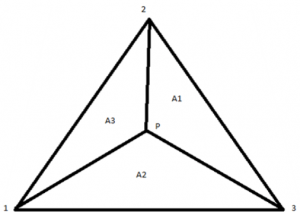
a) s1=A1/(A1+A2+A3)
b) s1=(A1+A2+A3)/A1
c) s1=A1+A2+A3
d) s1=A1
View Answer
Explanation: For A1, A2, and A3 as area coordinates and s1, s2 and s3 as shape functions for the element shown, the total area is equal to the sum of A1, A2 and A3 and s1 is calculated by the relation s1=A1/total area
=A1/(A1+A2+A3).
5. In Finite Element Methods (FEM), In two-dimensional problems, we shall have two types of errors, one due to the approximation of the solution and the other due to approximation of the domain.
a) True
b) False
View Answer
Explanation: In two-dimensional problems, the finite elements are simple geometric shapes that can be used to approximate a given domain as well as the solution over it. We not only approximate solution on a domain but also the domain itself by using a suitable mesh. As a result, we shall have two types of errors, one due to the approximation of the solution and the other due to approximation of the domain.
6. For A1=5, A2=10, A3=5, what is the value of the shape function at node 1 of the triangular element shown?

a) 0.15
b) 0.25
c) 0.35
d) 0.45
View Answer
Explanation: Total area is A.
A=A1+A2+A3
A=5+10+5
=20.
The shape function at node 1 is given by (A1/A)
=5/20
=0.25.
7. If x1, x2 and x3 are displacements of nodes 1, 2 and 3 respectively and e, n are shape functions then which expression correctly describes displacement of any point(x,y) on the element along x direction?
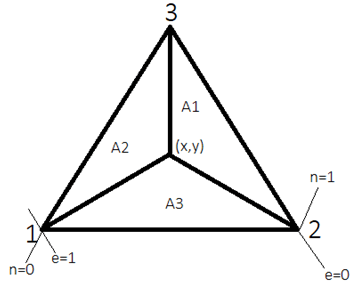
a) x=(x1-x3)e+(x2-x3)n+x3
b) x=n*x1+e*x2+x3
c) x=(x1–x2)e+(x2-x3)n+x3
d) x=(x1–x2)e+(x1-x3)n+x3
View Answer
Explanation: A triangular element has three nodes and hence three shape functions. Here, the three shape functions are shown as e,n and 1-e-n. Thus, displacement of any point(x,y) on element along x direction is x=(x1*e)+(x2*n)+x3*(1-n-e) or x=(x1-x3)e+(x2-x3)n+x3.
8. u=u[x(e,n),y(e,n)] and v=v[x(e,n),y(e,n)] Using the chain rule of partial derivatives, we get Jacobian of the transformation, J. The relation between area (A) of 2D three noded triangular element and Jacobian is given by _____
a) A=1*|detJ|
b) A=(1/3)*|detJ|
c) A=0.5*|detJ|
d) A=2*|detJ|
View Answer
Explanation: For a 2D three noded triangular element area A=(0.5)*|(x1-x3)*(y2-y3)-(x2-x3)*(y1-y3)|. Using the chain rule of partial derivatives, we get Jacobian of the transformation, J=\(\begin{pmatrix}x1-x3&x2-x3\\y1-y3&y2-y3\end{pmatrix}\). Then detJ=(x1-x3)*(y2-y3)-(x2-x3)*(y1-y3) and in terms of detJ
A=A=0.5*|detJ|
9. In a two-dimensional static structural problem, the various non-zero stresses are ____
a) σ=[σxσyσz]
b) σ=[σxσyσx+σy]
c) σ=[σxσyσx-σy]
d) σ=[σxσyτxy]
View Answer
Explanation: In a two-dimensional static structural problem, the stresses are in a single plane.They are the two normal stresses σx, σy and one shear stress τxy.
10. If 1, 2 and 3 is the order of sequence of elemental nodes of e=1 then to make elemental connectivity, which of the following is the correct order for e=2?
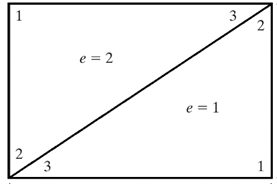
a) 2 3 1
b) 1 3 2
c) 3 2 1
d) 2 1 3
View Answer
Explanation: Since, the order of nodes for e=1 is in counter clockwisesense, the same has to be followed for ordering the nodes of e=2. Thus, 2 3 1 is the correct option.
11. If 1, 2; 3, 4; 5, 6 and 7, 8 are the degrees of freedom at nodes 1,2,3 and 4 respectively then the common degrees of freedom for e=1 and e=2 are ____
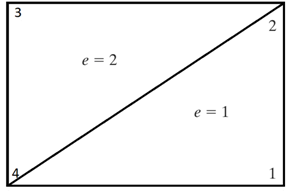
a) 3 4, 7 8
b) 1 2, 3 4
c) 5 6, 7 8
d) 1 2, 5 6
View Answer
Explanation: The common degrees of freedom for e=1 and e=2 are the one corresponding to common nodes between e=1 and e=2. The common nodes are 2 and 3. Thus, the common degrees of freedom are 3, 4 and 7, 8.
Sanfoundry Global Education & Learning Series – Finite Element Method.
To practice all areas of Finite Element Method, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Practice Civil Engineering MCQs
- Apply for Mechanical Engineering Internship
- Check Mechanical Engineering Books
- Practice Mechanical Engineering MCQs
- Check Finite Element Method Books
