This set of Finite Element Method Multiple Choice Questions & Answers (MCQs) focuses on “One Dimensional Problems – Temperature Effects”.
1. With temperature effect which will vary linearly?
a) Horizontal stress load
b) Potential energy
c) Vertical stress load
d) Kinematic energy
View Answer
Explanation: Temperature is a variant which varies from one point to another point. It has adverse effects on different structures. By temperature effect Vertical stress load vary linearly.
2. α means ____
a) Co-efficient of thermal expansion
b) Co-efficient of linear expansion
c) Thermal expansion
d) Thermal effect
View Answer
Explanation: The co-efficient of thermal expansion describes how the size of an object changes with a change in temperature. Specifically, it measures the fractional change in size per degree change in temperature at constant pressure. It is denoted by symbol α.
3. In temperature effect, initial strain, ε0= ____
a) α ΔT
b) α+ΔT
c) α-ΔT
d) Load
View Answer
Explanation: Strain is relative change in shape or size of an object due to externally applied forces. Temperature is a variant which varies from one point to another point. In temperature effect of FEM, Initial strain ε0=α ΔT.
4. In a structure, a crack is formed as a result of ______
a) Thermal expansion
b) Thermo couple
c) Thermal strain
d) Thermal stress
View Answer
Explanation: Thermal stress is caused by differences in temperature or by differences in thermal expansion. A crack formed as a result of Thermal stress produced by rapid cooling from a high temperature.
5. In the given diagram, the line indicates ____________
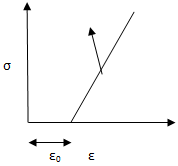
a) Stress relation
b) Strain relation
c) Stress – strain relation
d) Undefined
View Answer
Explanation: Stress is physical quantity that expresses the internal forces that neighboring particles of a continues material exert on each other. While, strain is the measure of deformation of the material. In the given diagram, the line indicates Stress-strain relation.
6. Stress – strain relation is given as _____
a) σ=E
b) σ=Eε
c) σ=E(ε-ε0)
d) Undefined
View Answer
Explanation: Stress is a physical quantity that expresses the internal forces that neighboring particles of a continuous material exert on each other, while strain is the measure of the deformation of the material. Stress- strain relation is given as
σ=E(ε-ε0).
7. Strain energy per unit volume is ___
a) u0=E(ε-ε0)
b) u0=\(\frac{1}{2}\)E(ε-ε0)
c) Non symmetric
d) Specified displacement
View Answer
Explanation: Energy stored in a body due to deformation is called Strain energy. The strain energy per unit volume is called strain energy density and the area under the stress strain curve towards the point is deformation. Strain energy per unit volume is
u0=\(\frac{1}{2}\)E(ε-ε0)
8. Temperature change is denoted as_____
a) ΔT=(T2-T1)
b) θe
c) le
d) Ae
View Answer
Explanation: Temperature is the measure of average kinetic energy of the particles in a system. Adding heat to system causes temperature rise. In Finite element analysis temperature is denoted as θe.
9. θe=\(\frac{E_eA_el_e\alpha\Delta T}{x_2-x_1}\begin{Bmatrix}-1 \\ 1 \end{Bmatrix}\) is the temperature effect.
a) True
b) False
View Answer
Explanation: Temperature is the measure of average kinetic energy of the particles in a system. Adding heat to system causes its temperature to rise. Temperature effect describes that how much of temperature is rised in body when load is applied. Temperature effect formula is as shown
θe=\(\frac{E_eA_el_e\alpha\Delta T}{x_2-x_1}\begin{Bmatrix}-1 \\ 1 \end{Bmatrix}\).
10. Stress in each element is ____
a) Eliminated
b) σ=EBq
c) σ=αΔT
d) σ=E(Bq-αΔT)
View Answer
Explanation: Stress is a physical quantity that expresses the internal forces that neighboring particles of a continuous material exert on each other. After solving Finite element equations KQ=F for the displacements Q, the stress in each element can be obtained from equation.
σ=E(Bq-αΔT).
Sanfoundry Global Education & Learning Series – Finite Element Method.
To practice all areas of Finite Element Method, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Practice Mechanical Engineering MCQs
- Check Finite Element Method Books
- Check Mechanical Engineering Books
- Apply for Civil Engineering Internship
- Practice Civil Engineering MCQs
