This set of Finite Element Method Multiple Choice Questions & Answers (MCQs) focuses on “Beams with Axial Loading”.
1. What is the deformation of a steel bar subjected to an axial load of 100N? Parameters are given as follows: Area = 100mm2, Young’s Modulus = 210 GPa, Length of bar = 1m.
a) 0.00476mm
b) 47.46mm
c) 4.746mm
d) .00328mm
View Answer
Explanation: Deformation = PL / AE
P = 100N, L = 1000mm, A = 100mm2, E = 210 * 103MPa
Deformation = (100 * 1000) / (100 * 210 * 103)
Therefore, Deformation = 0.00476mm
2. According to Euler – Bernoulli Beam Theory, Normal stress parallel to the cross – sectional plane is equal to zero.
a) False
b) True
View Answer
Explanation: The Euler – Bernoulli Beam Theory has a total of 3 assumptions. They are:
i) Cross sections of beam do not show any significant deformation under the application of transverse or axial loads.
ii) Normal stress parallel to the cross – sectional plane is equal to zero.
iii) During deformation, the cross section of the beam is assumed to remain planar and normal to the deformed axis of the beam.
3. What is the main difference between the Timoshenko Beam Theory and Euler – Bernoulli Beam Theory?
a) Both are the same
b) Shear deformations in Timoshenko Beam Theory are zero values
c) Shear deformations in Euler – Bernoulli Beam Theory are nonzero values
d) Shear deformations in Timoshenko Beam Theory are nonzero values
View Answer
Explanation: The two beam theories under consideration are given utmost importance while solving any beam related problems. In Euler – Bernoulli Beam Theory, the shear deformations are zero values; whereas in the Timoshenko Beam Theory, shear deformations are nonzero values.
4. Which of the following is not an assumption of Timoshenko Beam Theory?
a) Shear stress at a specific cross section is constant
b) Normal stress parallel to cross sectional plane is not equal to zero
c) Change of depth of cross section is neglected while determining axial displacement
d) Normal stress parallel to cross sectional plane is equal to zero
View Answer
Explanation: According to the Timoshenko Beam Theory, Normal stress parallel to cross sectional plane is equal to zero. Hence, the statement is false and fails to satisfy the assumptions of the Timoshenko Beam Theory.
5. Find out the total displacement of the beam shown in figure below. Parameters are given as follows: d1 = 50mm, L1 = 200mm, d2 = 40mm, L2 = 100mm, E = 2 * 105Mpa.
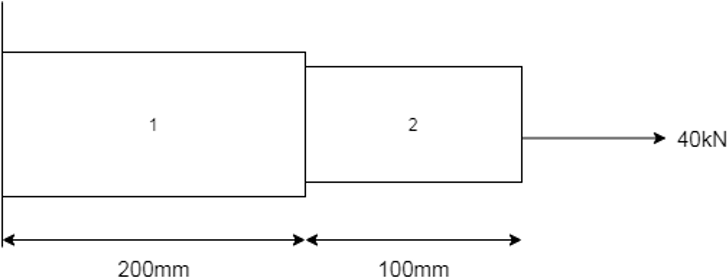
a) 36.35mm
b) 3.62mm
c) 0.0362mm
d) 363.5mm
View Answer
Explanation: Total displacement = Displacement1 + Displacement2
Displacement = PL / AE
Displacement1 = (40 * 103 * 200) / ((pi * 502 / 4) * 2 * 105) = 0.0203mm
Displacement2 = (40 * 103 * 100) / ((pi * 402 / 4) * 2 * 105) = 0.0159mm
Total Displacement = .0203 + .0159 = 0.0362mm
6. Linear Buckling Analysis is applicable for Axial loads.
a) True
b) False
View Answer
Explanation: Linear Buckling Analysis is only applicable for Compressive Loads; hence the given statement is false. Buckling Analysis is a special case scenario, which takes buckling failure that arises only because of compressive loads into consideration. It is further divided into Elastic and Non – Elastic Buckling.
7. What is the stress acting on a body if it is acted upon by an axial load of 196.2N? The area of the body is 500mm2.
a) 0.3924
b) 39.24
c) 45.16
d) 0.4516
View Answer
Explanation: Stress = Force / Area
Force = 196.2N, Area = 500mm2
Stress = Force / Area = 196.2 / 500 = 0.3924 N / mm2
8. Which of the following do not fall under axial loading conditions?
a) Tension
b) Compression
c) Bending and torsion
d) Uniformly distributed load
View Answer
Explanation: Tension, Compression and Uniformly distributed load fall under axial loading conditions, as the force is acting along the axis of the structure. Bending acts perpendicular to the axis of structure, whereas torsion acts radial to the axis of the structure.
9. Find out the axial load if the deformation produced = .05mm. Parameters are given as follows: Area = 200mm2, Young’s Modulus = 200 GPa, Length of bar = 2m.
a) 100N
b) 10N
c) 1000N
d) 156N
View Answer
Explanation: Deformation = PL / AE
Given, Area (A) = 200mm2, Young’s Modulus (E) = 200 GPa, Length of bar (L) = 2m, Deformation = .05mm
Therefore, Load(P) = (Deformation * AE) / L
Load = (.05 * 200 * 200 * 103) / 2000
Load = 1000N
10. Which of the following is not a stage of the Fatigue fracture phenomenon?
a) Final Rupture
b) Sintering
c) Propagation
d) Initiation
View Answer
Explanation: Sintering is not a stage of the Fatigue fracture phenomenon. It corresponds to the process of compacting and forming of solid materials on application of heat and pressure. Initiation, Propagation and Final Rupture are the three stages of fatigue fracture. Fatigue fracture refers to the process by which cracks are developed in the material due to the application of cyclic loads.
Sanfoundry Global Education & Learning Series – Finite Element Method.
To practice all areas of Finite Element Method, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Apply for Mechanical Engineering Internship
- Check Civil Engineering Books
- Check Mechanical Engineering Books
- Apply for Civil Engineering Internship
- Practice Mechanical Engineering MCQs
