This set of Finite Element Method Multiple Choice Questions & Answers (MCQs) focuses on “Interpolation Functions – Triangular, Rectangular, and Three-Dimensional Elements”.
1. Which of the following is not an example of a triangular element?
a) Single node linear
b) 3 node linear
c) 6 node quadratic
d) 10 node cubic
View Answer
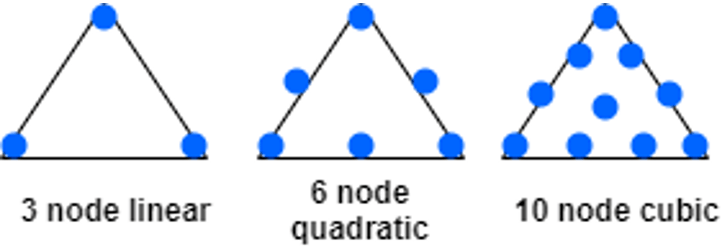
Explanation: Single node linear is not an example of a triangular element. The other three types of triangular elements are depicted in the figure below.
2. What is the function of an internal node in case of the cubic element?
a) To attain a symmetric shape
b) To attain geometrical isotropy
c) To satisfy mesh refinement
d) To nullify geometrical errors
View Answer
Explanation: An internal node is one that stays interior to the element and is not connected to any other node. In case of the cubic element, the internal node is required to satisfy geometric isotropy which allows the functional form to stay constant in both translational and rotational forms.
3. In structural applications, what is a constraint strain element?
a) 4 node rectangular element
b) 6 node triangular element
c) 3 node triangular element
d) 8 node rectangular element
View Answer
Explanation: In case of structural applications, the 3 noded triangular elements are also referred to as constraint strain elements(CST) . It has various advantages. For instance, in case of heat transfer problems, it helps produce constant temperature gradients, which in turn oversee constant heat flow in the element.
4. Which of the following defines area coordinates?
a) Location of area in the arbitrary plane
b) Ratio of assumed area to total area
c) They are nothing but the respective nodal areas
d) Ratio of nodal area to total area
View Answer
Explanation: Area coordinates can be computed by finding out the ratio of nodal areas to the total areas. As triangular elements computation is complex and cumbersome, simplification of interpolation functions is required. This is satisfied by making use of these area coordinates.
5. Rectangular elements are singular and cannot be used with other elements.
a) True
b) False
View Answer
Explanation: The given statement is false. Rectangular elements are not singular, and can be used along with other elements. In fact, for many geometries it is preferred to have rectangular elements in conjunction with triangular or other types of elements for development of quadrilateral structures.
6. Which of the following is an example of a rectangular element?
a) 4 noded rectangle
b) 3 noded triangle
c) Multi node circle
d) 4 noded triangle
View Answer
Explanation: The 4 noded rectangle is an example of the rectangular element. It is generally assumed that the sides of the rectangle are parallel to the global Cartesian axes. It is depicted as follows –

7. What is considered as the equivalent of area coordinates incase of rectangular elements?
a) Area elements
b) Area nodes
c) Natural coordinates
d) Isolated coordinates
View Answer
Explanation: Incase of rectangular elements, to simplify calculations natural/serendipity coordinates are used. This is because, the complexity incase of rectangular elements can be reduced by making judicious choice of the coordinates.
8. How are higher order rectangular elements developed?
a) Continuous interpolation is done
b) Existing node is subtracted
c) Mesh refinement is done
d) Additional nodes are added
View Answer
Explanation: In order to develop higher order rectangular elements, an additional node is added at the midpoint of each side of the element. This method has its disadvantages too. Pascal triangle shows that we cannot construct a complete polynomial having 8 terms, but can be accomplished by making use of two incomplete, symmetric cubic polynomials.
9. What are considered as the two main families of three dimensional elements?
a) Tetrahedrons and Parallelepipeds
b) Tetrahedrons and Rectangles
c) Parallelepipeds and Triangles
d) Tetrahedrons only
View Answer
Explanation: Tetrahedrons and Parallelepipeds are considered as the two main families of three dimensional elements. While tetrahedrons are extension of triangular elements, the parallelepipeds are extensions of rectangular elements. Parallelepipeds are otherwise referred to as brick elements.
10. Which of the following is the definition of volume coordinates?
a) Specific total volume
b) Ratio of nodal volume to the total volume
c) Unit total volume
d) Ratio of total volume to element volume
View Answer
Explanation: A volume coordinate is defined as the ratio of nodal volume to the total volume. Their role is similar to that of area coordinates incase of triangular elements and natural coordinates incase of rectangular elements. They help in simplifying the computation procedures.
11. In structural applications, which of the following element is considered as the constant strain element?
a) Triangular element
b) Hexagonal element
c) Tetrahedral element
d) Brick element
View Answer
Explanation: Incase of structural applications, the tetrahedral element is considered as the constant strain element. This is because, all first partial derivatives of the field variable are constant. This element is also considered most useful for use in irregular geometries.
Sanfoundry Global Education & Learning Series – Finite Element Method.
To practice all areas of Finite Element Method, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Practice Civil Engineering MCQs
- Check Civil Engineering Books
- Check Finite Element Method Books
- Practice Mechanical Engineering MCQs
- Apply for Mechanical Engineering Internship
