This set of Finite Element Method Multiple Choice Questions & Answers (MCQs) focuses on “Single Variable Problems – Applications – 1”.
1. If the finite element model shown below represents heat conduction in axisymmetric or plane geometries then which option is not true?
\(-\frac{\partial}{\partial x}(a_{11}\frac{\partial u}{\partial x}+a_{12}\frac{\partial u}{\partial y})-\frac{\partial}{\partial y}(a_{21}\frac{\partial u}{\partial x}+a_{22}\frac{\partial u}{\partial y})\) +a00u-f=0
a) u is temperature
b) a11, a22 are conductivities in x, y directions
c) f is internal heat generation
d) a00=1
View Answer
Explanation: Given model equation is a 2nd order partial differential equation. For heat conduction in axisymmetric or plane geometries, the given model equation is applicable for u as temperature, a11 and a22 as conductivities in x and y directions respectively, f as internal heat generation and a00=0.
2. In steady state heat transfer finite element model [K+H]*{T}={Q}*{P} if convective boundary conditions are neglected then which option is applicable?
a) K=0
b) H=0
c) Q=0
d) T=0
View Answer
Explanation: When convective boundary conditions are neglected in the steady state heat transfer finite element model [K+H]*{T}={Q}*{P}, it reduces to [K]*{T}={Q} form. The terms H and P which are related to convection become zero.
3. For a convective boundary, the natural boundary condition is a balance of energy transfer across the boundary due to conduction and/or convection.
a) True
b) False
View Answer
Explanation: The existence of convection heating or cooling leads to the convection boundary condition, known as Newton boundary condition. For a convective boundary, the natural boundary condition is a balance of energy transfer across the boundary due to conduction and/or convection.
4. In the below equation for steady-state heat transfer in plane systems, what does β stands for?
\(k_x\frac{\partial T}{\partial x}n_x+k_y\frac{\partial T}{\partial y}n_y\)+β(T-T∞)=\(\hat{q}\)n
a) Convective heat transfer coefficient
b) Thermal expansion
c) Thermal conductivity
d) Diffusivity
View Answer
Explanation: The existence of convection heating or cooling leads to the convection boundary condition, known as Newton boundary condition. For a convective boundary, the natural boundary condition is a balance of energy transfer across the boundary due to conduction and/or convection. β stands for convective conductance (or the convective heat transfer coefficient).
5. In a steady state heat conduction problem with a thermal conductivity of 22(W/(m*K)), for a typical element of mesh of linear triangular elements, what is the value of a in stiffness matrix,
K=a*\(\begin{pmatrix}
1&-1&0\\-1 & 2 & -1\\0 & -1 & 1\end{pmatrix}\)?
a) 11
b) 12
c) 10
d) 5.5
View Answer
Explanation: For a typical element of mesh of linear triangular elements K=(k/2)*\(\begin{pmatrix}
1&-1&0\\-1 & 2 & -1\\0 & -1 & 1\end{pmatrix}\) denotes the element coefficient matrix. Given thermal conductivity (k) is 22 then
a=k/2
a=22/2
=11.
6. Heat conduction problem over a rectangular domain is shown in figure. Which nodes have temperature value of zero units?
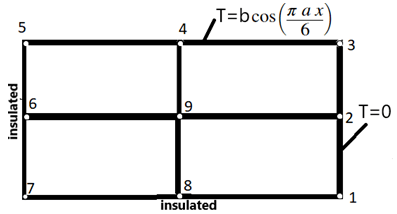
a) Only1
b) Only 7
c) Only 2 and 3
d) 1, 2 and 3
View Answer
Explanation: All the nodes present at the boundary along which temperature value is zero will have T=0. In the given domain, the nodes 1, 2 and 3 are on boundary with temperature value zero. The node 7 is along an insulated boundary where temperature value depends on the temperature of other boundaries.
7. If q denotes the amount of heat flow through any boundary then what is the value of q at node7?

a) Dependent on a,b
b) =0
c) >0
d) <0
View Answer
Explanation: A boundary which is insulated will have no heat flow. Thus All the nodes present at that boundary will have q=0, irrespective of the value of T at other boundaries. In the given domain, the nodes 6, 7 and 8 are on insulated boundary, thus no heat flow.
8. What is the value of T at node 3 if the length of each element is 1/a units?
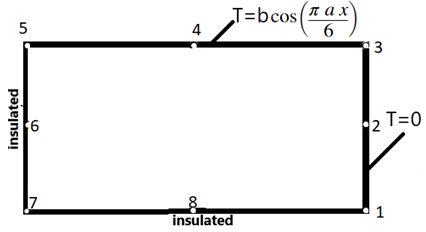
a) 0.5*b
b) b
c) 2*b
d) b*cos(a)
View Answer
Explanation: Given that the temperature distribution at boundary follows T=bcos\(\frac{\pi ax}{6}\).
At node 3, x=2/a units,
ax=2
T=bcos\(\frac{\pi2}{6}\)
T=bcos\(\frac{\pi}{3}\)
=b*0.5.
9. The velocity field of a fluid flow is denoted by v=2xi+3j. Which option exactly describes the flow?
a) Ideal
b) Compressible
c) Irrational
d) Inviscid
View Answer
Explanation: A fluid is said to be incompressible if ∇.V=0.
∇.V=\(\frac{d(2x)}{dx}+\frac{d(3)}{dy}\)
=2+0
=2.
Thus, the flow is compressible.
10. For a two dimensional problem, the evaluation of boundary integrals amounts to evaluation of line integrals.
a) True
b) False
View Answer
Explanation: The boundary of a 2D element consists of line segments, which are one dimensional elements. Thus, for a two dimensional problem, the evaluation of boundary integrals amounts to evaluation of line integrals (one dimensional elements).
11. A river flows along node 1 through node 4, infiltrating an aquifer at constant rate of 5(m3/day*m2). The length of elements is 0.2m. What is the value of global force due to infiltration of the river at node 1?
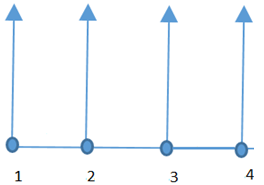
a) 0.5
b) 1.0
c) 1.5
d) 2.0
View Answer
Explanation: The value of global force due to infiltration of the river at node 1 is given by 0.5*q*h, where 0.5 denotes the value of the shape function, q is rate of infiltration and h is length of the element.
=0.5*q*h
Given q=5, h=0.2
=0.5*5*0.2
=0.5.
12. In a Heat Transfer problem, which option is used for interpolation of temperature inside a finite element?
a) Natural coordinates
b) Global coordinates
c) Temperature gradients
d) Shape functions
View Answer
Explanation: Shape Functions are used for interpolation of temperature inside a finite element. Global coordinates are used to apply boundary conditions. Natural coordinates are used to derive shape functions. Temperature gradients can’t be used for interpolation.
13. Consider a system where a wall of a tank containing a hot liquid at a temperature T0, with an air stream of temperature T∞ flows on the outside of the tank, maintaining the outside wall temperature of TL. What is the expression for boundary condition of the system?
a) q=h(TL-T∞)
b) T=T∞
c) T=TL
d) TL-T∞
View Answer
Explanation: The boundary conditions are mainly of three kinds: constant temperature, constant heat flux (zero for insulated), and convection. In this problem, the temperature difference between wall and surroundings creates the constant heat flux of q=h(TL-T∞). This heat flux is taken as a boundary condition.
Sanfoundry Global Education & Learning Series – Finite Element Method.
To practice all areas of Finite Element Method, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Check Finite Element Method Books
- Apply for Civil Engineering Internship
- Practice Civil Engineering MCQs
- Check Civil Engineering Books
- Apply for Mechanical Engineering Internship
