This set of Finite Element Method Multiple Choice Questions & Answers (MCQs) focuses on “Governing Equations”.
1. For fluid flows, which expression does not characterize the slow flow of a viscous and incompressible fluid in a closed domain?
a) v.∇v=0
b) μ≠0
c) =0
d) =0
View Answer
Explanation: The slow flow of a viscous and incompressible fluid in a closed domain is characterized by the following expressions:
Slow (inertial effects are negligible): v.∇v=0.
Viscous: μ≠0.
Incompressible: =0.
It is not a uniform flow; thus, ≠0.
2. In mathematical modeling, for which option, a fluid flow can be approximated by a two-dimensional model?
a) One of the dimensions is very small, and there is some flow along with it
b) One of the dimensions is very long, and there is no flow along with it
c) One of the dimensions is very long, and there is some flow along with it
d) The velocity components in two directions vary along the third direction
View Answer
Explanation: For a fluid flow, assuming that one of the dimensions say, along the z-direction (into the plane of the screen) of the domain is very long, and there is no flow along that direction. The velocity components in the other two directions (vx and vy) do not vary with the z-direction. Under these conditions, the flow can be approximated by a two-dimensional model.
3. For fluid flows obeying conservation of mass, what is the value of k if v=4x+ky denotes the velocity at any point in the flow?
a) -4
b) 4
c) -2
d) 2
View Answer
Explanation: A flow obeys conservation of mass if \(\frac{\partial v_x}{\partial x}+\frac{\partial v_y}{\partial y}\)=0. Comparing v=4x+ky with v=vx+vy, we get vx=4x and vy=ky.
Using the conservation of mass, we get \(\frac{\partial (4x)}{\partial x}+\frac{\partial (ky)}{\partial y}\)=0
4+k=0
K=-4.
4. The following equation represents the momentum equation for a fluid flow that is approximated by a two-dimensional model. What does k stand for?
ρ\(\frac{\partial v_x}{\partial t}-\frac{\partial}{\partial x}(2k\frac{\partial v_x}{\partial x})-\frac{\partial}{\partial y}[k(\frac{\partial v_x}{\partial y}+\frac{\partial v_y}{\partial x})]+\frac{\partial P}{\partial x}\)-fx=0
a) Thermal conductivity
b) Fluid viscosity
c) Density
d) Pressure
View Answer
Explanation: By using constitutive relations the momentum equation is expressed as ρ\(\frac{\partial v_x}{\partial t}-\frac{\partial}{\partial x}(2k\frac{\partial v_x}{\partial x})-\frac{\partial}{\partial y}[k(\frac{\partial v_x}{\partial y}+\frac{\partial v_y}{\partial x})]+\frac{\partial P}{\partial x}\)-fx=0, where vx, vy are the velocity components, P is the pressure, k is the viscosity, fx is the component of the body force vector, and ρ is the density.
5. If a finite element model involves the natural and direct formulation of momentum and continuity equations, then it is known as the velocity-pressure formulation or mixed formulation.
a) True
b) False
View Answer
Explanation: There are two different finite element models of momentum and continuity equations. The first one is a natural and direct formulation of momentum and continuity equations. It is known as the velocity-pressure formulation or mixed formulation. The second model is based on the interpretation that the continuity equation is an additional relation among the velocity components.
6. In the formulation of the finite element model for fluids flows, which option is not correct about the penalty formulation?
a) The continuity equation is an additional relation among the velocity components
b) The constraint is satisfied in an approximate sense
c) Uses the penalty function method
d) Involves natural and direct formulation of momentum and continuity equations
View Answer
Explanation: There are two different finite element models of momentum and continuity equations. The penalty formulation is based on the interpretation that the continuity equation is an additional relation among the velocity components. The constraint is satisfied in a least-squares (i.e., approximate) sense. This particular method of including the constraint in the formulation is known as the penalty function method. It does not involve the natural and direct formulation of momentum and continuity equations.
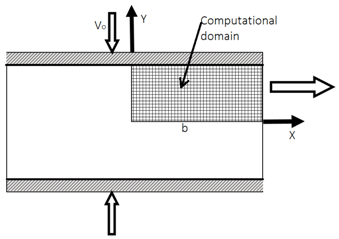
7. Consider the unsteady flow of a viscous fluid squeezed between two horizontal parallel plates, as shown in the following figure. The flow is induced by the uniform motion of the plates toward each other. What are the boundary conditions at the boundary ‘b’ of the domain if vx, vyare the velocity components?
a) vy≠0 and vx≠0
b) vy=0 and vx≠0
c) vy≠0 and vx=0
d) vy=0 and vx=0
View Answer
Explanation: For the unsteady flow of a viscous fluid squeezed between two horizontal parallel plates, because of the symmetry, the computational domain is taken to be one-quarter of the flow field. Since the boundary ‘b’ is located equidistant from the plates, the pushing effect of one plate balances the pushing effect from the opposite one and results in a vertical constraint (vy=0) for the plate. The fluid is free to move in a horizontal direction, thus, vx≠0.
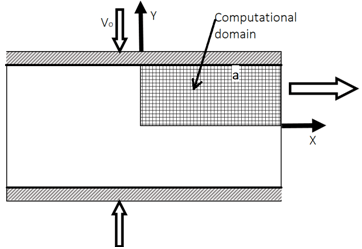
8. Consider the unsteady flow of a viscous fluid squeezed between two horizontal parallel plates, as shown in the following figure. The flow is induced by the uniform motion of the plates toward each other. What are the boundary conditions at the boundary ‘a’ of the domain if vx, vyare the velocity components?
a) vy=-V0 and vx=0
b) vy=-V0 and vx≠0
c) vy=V0 and vx=0
d) vy=V0 and vx≠0
View Answer
Explanation: For the unsteady flow of a viscous fluid squeezed between two horizontal parallel plates, because of the symmetry, the computational domain is taken to be one-quarter of the flow field. The top plate has a velocity –V0. The fluid along the top plate is imparted –V0 along the vertical direction and zero velocity (no slip condition) in the horizontal direction, thus vy=-V0 and vx=0.
9. Which statement is not true regarding the variables present in the viscous flow problems?
a) Velocity components are zero on fixed walls
b) Shear stress is zero along the line of symmetry
c) Vertical velocity component vy and horizontal stress tx must be zero along the horizontal line of symmetry
d) Shear stress is non zero along the line of symmetry
View Answer
Explanation: In general, the primary variables are obtained using FEM and secondary variables are calculated using the primary variables. In the viscous flow, both the velocity components are zero on fixed walls, and shear stress is zero along the line of symmetry. Vertical velocity component vy and horizontal stress tx must be zero along the horizontal line of symmetry and vx, ty must be zero along the vertical line of symmetry.
10. Considering the problem of (linear) bending of beams according to the Euler-Bernoulli beam theory, if the beam is in equilibrium, then solving the equations governing the equilibrium of the Euler-Bernoulli beam is equivalent to minimizing the total potential energy.
a) True
b) False
View Answer
Explanation: Consider the problem of (linear) bending of beams according to the Euler-Bernoulli beam theory. The principle of minimum total potential energy states that if the beam is in equilibrium, then the total potential energy associated with the equilibrium configuration is the minimum; i.e., the equilibrium displacements make the total potential energy a minimum. Thus, solving the equations governing the equilibrium of the Euler-Bernoulli beam is equivalent to minimizing the total potential energy.
Sanfoundry Global Education & Learning Series – Finite Element Method.
To practice all areas of Finite Element Method, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Check Civil Engineering Books
- Apply for Civil Engineering Internship
- Check Mechanical Engineering Books
- Check Finite Element Method Books
- Practice Civil Engineering MCQs
