This set of Finite Element Method Multiple Choice Questions & Answers focuses on “Boundary Value Problems – 2”.
1. For A1=5, A2=10, A3=5, what is the value of the shape function at node 1 of the element shown?
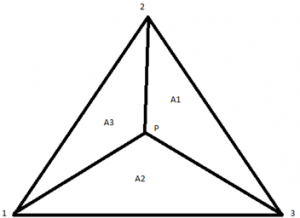
a) 0.15
b) 0.5
c) 0.35
d) 0.25
View Answer
Explanation:
Total area, A=A1+A2+A3
A=5+10+5
=20.
The shape function at node 2 is given by (A2/A)
=10/20
=0.5.
2. In a solid of revolution, if the geometry, support conditions, loads, and material properties are all symmetric about the axis and are independent of θ, then the problem can be treated as a ____
a) two-dimensional one
b) one-dimensional one
c) three-dimensional one
d) plane strain
View Answer
Explanation: In a solid of revolution, if the geometry, support conditions, loads, and material properties are all symmetric about the axis and are independent of θ, then the problem can be treated as a two-dimensional problem. Moreover, due to the absence of stress variation in the third dimension, such a problem is treated as a plain stress problem.
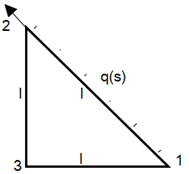
3. A function Q is evaluated at boundary 1-2 by boundary integral Q=∮q(s)*S(s)ds where q(s)=q0 and shape functions S(s) are S1, S2.S1=1-(s/l) and S2=1-S1 then Q1 is given by expression ____
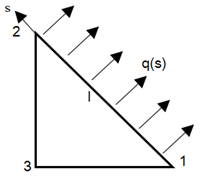
a) \((\frac{1}{2})\)*q0*l
b) q0*l
c) \((\frac{1}{3})\)*q0*l
d) \((\frac{1}{6})\)*q0*l
View Answer
Explanation: Given Q=∮q*S(s)ds
Q1=\(\int_{0}^l\)q(s)*S1*ds
=\(\int_{0}^l\)q0*(1-\((\frac{s}{l}))\)*ds
=[q0*s*(1-\( (\frac{s}{2*1})\))]
Putting limits of s from zero to l
Q1=[(1-\(\frac{1}{2}\))*q₀*l]-0
=\((\frac{1}{2})\)*q₀*l.
4. In a static structural type Boundary Value Problem, at any fixed support, How many non-zero Degrees Of Freedom exist?
a) 0
b) 1
c) 2
d) 3
View Answer
Explanation: In a static structural type Boundary Value Problem, three types of supports exist. They are roller, fixed and hinged support. A fixed support has zero degrees of freedom where as a roller and a hinged support have two and one degree of freedom respectively.
5. A function Q is evaluated at boundary 1-2 by boundary integral Q=∮q(s)*S(s)ds where q(s)=q0 and shape functions S(s) are S1, S2.S1=1-(s/l) and S2=1-S1 then Q3 is given by the value ____
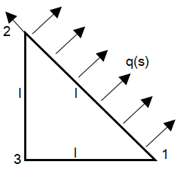
a) \((\frac{1}{2})\)
b) 1
c) \((\frac{1}{3})\)
d) 0
View Answer
Explanation: Given Q=∮q*S(s)ds
Since there is no q(s) defined on sides 2-3 and 3-1 we take q(s)=0.
Q3=\(\int_{0}^l\)0*S1*ds
=0.
6. In a static structural type Boundary Value Problem, at any roller support, How many non-zero Degrees Of Freedom exist?
a) 0
b) 1
c) 2
d) 3
View Answer
Explanation: In a static structural type Boundary Value Problem, three types of supports exist. They are roller, fixed and hinged support. A fixed support has zero degrees of freedom where as a roller and a hinged support have two and one degree of freedom respectively.
7. A function Q is evaluated at boundary 1-2 by boundary integral Q=∮q(s)*S(s)ds where q(s)=q0*(s/l) and shape functions S(s) are S1, S2.S1=1-(s/l) and S2=1-S1 then Q1 is given by expression ___
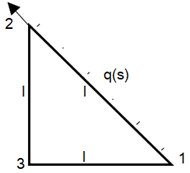
a) \((\frac{1}{2})\)*q₀*l
b) q₀*l
c) \((\frac{1}{3})\)*q₀*l
d) \((\frac{1}{6})\)*q₀*l
View Answer
Explanation: Given Q=∮q*S(s)ds
Along line 1-2, Q1=\(\int_{0}^l\)q(s)*S1*ds
=\(\int_{0}^l\)q0*\((\frac{s}{l})\)*(1-\((\frac{s}{l}))\)*ds
\(\int_{0}^l\)q0*\((\frac{s}{l})*ds-\int_{0}^l\)q0\(((\frac{s}{l})^2)\)*ds
Putting limits of s from zero to l
Q1=\((\frac{1}{2})\)*q0*l-\((\frac{1}{3})\)*q0*l
=q₀*l*\(((\frac{1}{2})-(\frac{1}{3}))\)
=\((\frac{1}{6})\)*q₀*l.
8. In a static structural type Boundary Value Problem, at any hinged support, How many non-zero Degrees Of Freedom exist?
a) 0
b) 1
c) 2
d) 3
View Answer
Explanation: In a static structural type Boundary Value Problem, three types of supports exist. They are roller, fixed and hinged support. A fixed support has zero degrees of freedom where as a roller and a hinged support have two and one non-zero degree of freedom respectively.
9. A function Q is evaluated at boundary 1-2 by boundary integral Q=∮q(s)*S(s)ds where q(s)=q₀*(s/l) and shape functions S(s) are S1, S2.S1=1-(s/l) and S2=1-S1 then Q2 is given by expression ___
a) \((\frac{1}{2})\)*q₀*l
b) q₀*l
c) \((\frac{1}{3})\)*q₀*l
d) \((\frac{1}{6})\)*q₀*l
View Answer
Explanation: Given Q=∮q*S(s)ds
Along line 1-2, Q2 =\(\int_{0}^l\) q(s)*S2*ds
=\(\int_{0}^l q_0*(\frac{s}{l})*(\frac{s}{l})*ds\)
=\(\int_{0}^l*((\frac{s}{l})^2)*ds\)
Putting limits of s from zero to l
= \((\frac{1}{3})\)*q₀*l.
10. For a linear triangular element with (xi, yi) as the coordinates of the ith node of the element, which option denotes twice the Area of the triangle?
a) (x1y2 − x2y1) + (x2y3 − x3y2) + (x3y1 − x1y3)
b) (x1y2 – x3y1) + (x2y3 – x1y2) + (x3y1 – x2y3)
c) (x1y2 − x2y1) + (x2y3 − x3y2)
d) (x1y1 − x2y2) + (x2y2 − x3y3) + (x3y3 − x1y1)
View Answer
Explanation: A linear triangular element has 3 nodes. With (xi, yi) as coordinates of ith node, the twice of area is given by determinant of the matrix \(\begin{pmatrix}1&x1&y1\\1&x2&y2\\1&x3&y3\end{pmatrix}\)which equals to (x1y2 − x2y1) + (x2y3 − x3y2) + (x3y1 − x1y3).
11. For a linear triangular element with (xi, yi) as the coordinates of the ith node of the element the area=10units, the value of ∑αi from the standard relation αi+βiX+γiY=(2/3)*Area where X=∑xi, Y=∑yi is ___
a) 10
b) 20
c) 30
d) 40
View Answer
Explanation: A linear triangular element has 3 nodes. With (xi, yi) as coordinates of ith node, the twice of area is given by determinant of the matrix \(\begin{pmatrix}1&x1&y1\\1&x2&y2\\1&x3&y3\end{pmatrix}\) which equals to (x1y2 − x2y1) + (x2y3 − x3y2) + (x3y1 − x1y3). Then from the standard relation we have ∑αi = (x2y3 − x3y2) + (x3y1 − x1y3) + (x1y2 − x2y1)
=2*Area
=2*10
=20.
12. For a linear triangular element with (xi, yi) as the coordinates of the ith node of the element the area=10units, the value of ∑βi from the standard relation αi+βiX+γiY=(2/3)*Area where X=∑xi, Y=∑yi is ___
a) 0
b) 10
c) 20
d) 30
View Answer
Explanation: A linear triangular element has 3 nodes. With (xi, yi) as coordinates of ith node, the twice of area is given by determinant of the matrix \(\begin{pmatrix}1&x1&y1\\1&x2&y2\\1&x3&y3&\end{pmatrix}\) which equals to (x1y2−x2y1)+(x2y3−x3y2)+(x3y1−x1y3). Then from the standard relation we have ∑βi=(y2−y3)+(y3−y1)+(y1−y2)
=y2−y3+y3−y1+y1–y2
=0.
13. In a 3D axisymmetric solid, because of symmetry about the longitudinal axis, the stresses do not vary along ___ coordinate.
a) x
b) y
c) z
d) θ
View Answer
Explanation: In a 3D axisymmetric solid, because of the symmetry about the longitudinal z-axis, the stresses does not vary along circumferential direction i.e. along θ coordinate and such a problem can be treated as a two-dimensional problem.
14. For a linear triangular element with (xi, yi) as the coordinates of the ith node of the element the area=10units, the value of ∑γi from the standard relation αi+βiX+γiY=(2/3)*Area where X=∑xi, Y=∑yi is ___
a) 0
b) 10
c) 20
d) 30
View Answer
Explanation: A linear triangular element has 3 nodes. With (xi, yi) as coordinates of ith node, the twice of area is given by determinant of the matrix\(\begin{pmatrix}1&x1&y1\\1&x2&y2\\1&x3&y3\end{pmatrix}\) which equals to (x1y2−x2y1)+(x2y3−x3y2)+(x3y1−x1y3).Then from the standard relation we have ∑γi=−(x2−x3)−(x3−x1)−(x1 − x2)
=−x2+x3−x3+x1−x1+x2.
=0.
Sanfoundry Global Education & Learning Series – Finite Element Method.
To practice all areas of Finite Element Method, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Check Finite Element Method Books
- Practice Civil Engineering MCQs
- Check Civil Engineering Books
- Apply for Civil Engineering Internship
- Check Mechanical Engineering Books
