This set of Thermal Engineering Multiple Choice Questions & Answers focuses on “Reaction Turbines – 2”.
1. Which of the following graphs shows correct variation of efficiency of a Parson’s reaction turbine with respect to blade speed ratio?
a) 
b) 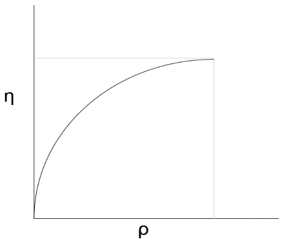
c) 
d) 
View Answer
Explanation: The correct variation of efficiency of Parson’s turbine with respect to the blade speed ratio (Cbl/C1) is shown by the following graph:

The maximum value of efficiency is reached when the blade speed ratio is equal to cosα.
2. Calculate the mean blade velocity of a Parson’s reaction turbine, if the steam leaves the nozzle with an absolute velocity of 320 m/s. Take the nozzle angle as 20° and the turbine works at maximum efficiency.
a) 156 m/s
b) 189 m/s
c) 256 m/s
d) 301 m/s
View Answer
Explanation: Given, C1 = 320 m/s, α = 20°
We know that, when a reaction turbine works at maximum efficiency
Cbl/C1 = cosα
Cbl = cosα*C1 = cos20*320 = 300.7 m/s ≈ 301 m/s.
3. The nozzle angle of a Parson’s reaction turbine is 25°. Determine the maximum possible efficiency for the turbine.
a) 75.62%
b) 84.56%
c) 90.19%
d) 93.21%
View Answer
Explanation: Given, α = 25°
Maximum possible value of efficiency for a Parson’s reaction turbine
ηmax = \(\frac{2(cos α)^2}{1+(cos α)^2} \)
ηmax = \(\frac{2(cos 25)^2}{1+(cos 25)^2} \) = 0.9019 or 90.19%.
4. The efficiency of steam turbine is greater than that of gas turbines.
a) True
b) False
View Answer
Explanation: Steam turbines work on Rankine cycle while the gas turbines on Brayton cycle. Rankine cycle is more efficient and close to Carnot cycle than Brayton cycle working between the same maximum and minimum temperatures.
5. The following data refer to a particular stage of a Parson’s reaction turbine:
Speed of the turbine = 1400 r.p.m.
Mean diameter of the rotor = 1 meter
Isentropic enthalpy drop = 8.530 kJ/Kg
Blade outlet angle = 20°
Speed ratio = 0.8
Determine the stage efficiency.
a) 56.32%
b) 65.75%
c) 78.74%
d) 84.79%
View Answer
Explanation: Given, N = 1400 r.p.m., D = 1 m, hd = 8.530 kJ/Kg, Ф = 20°, ρ = 0.8
Cbl = \(\frac{πDN}{60} = \frac{π*1*1400}{60}\) = 73.30 m/s
we know that,
ρ = \(\frac{C_{bl}}{C_1}\) 0.8 = \(\frac{73.30}{C_1}\) C1 = 91.63 m/s
For Parson’s reaction turbine,
α = Ф = 20°
Steps of Construction:
Select a suitable scale and draw a line LM to represent Cbl (= 73.30 m/s).
At point M, at an angle of 20° (α), cut a length MS to represent the velocity C1 (= 91.63 m/s). Join LS. Produce L to meet the perpendicular drawn from S at P. Thus inlet triangle is completed.
For a Parson’s turbine:
Cr2 = C1 = 91.63 m/s
and Ф = 20°
At L, at an angle of 20° (Ф), cut a length LN to represent Cr2 (= 91.63 m/s). Join MN.
Produce M to meet the perpendicular drawn from N at Q. Thus outlet triangle is completed.
By measurement:
Cw1 + Cw2 = 98.91 m/s
ηstage=\(\)\frac{C_{bl}(C_{w1}+C_{w2})}{h_d} = \frac{73.30(91.63)}{8530} = 0.7874 or 78.74%.
6. In a reaction turbine, the fixed blades and moving blades are of the same shape but reversed in direction. The angle of the discharging tip is 20°. The mean blade velocity is 200 m/s. The axial velocity of flow of steam is half of the mean blade velocity. Determine the inlet angles of blades.
a) 45°
b) 53°
c) 63°
d) 71°
View Answer
Explanation: Given, Cbl = 200 m/s, α = 20°
Cf1 = Cf2 = 0.5(Cbl) = 0.5(200) = 100 m/s
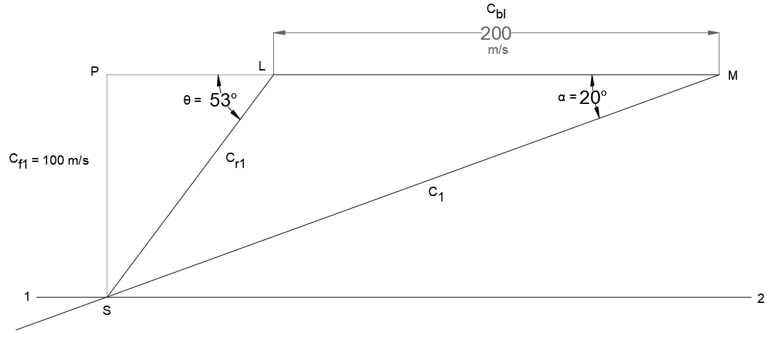
Steps of construction:
Select a suitable scale and draw a line LM to represent Cbl (= 200 m/s).
Draw line 1-2 parallel to line LM at a distance corresponding to 100 m/s from line LM.
At M, draw a line at an angle of 20° (α) to cut the line 1-2 at S. Join LS.
Produce L to meet the perpendicular drawn from S at P. Thus inlet triangle is completed.
By measurement:
θ = 53° (= Ф).
7. A 50% reaction turbine, having symmetrical velocity triangles, runs at 1500 r.p.m. The exit angles of the blades are 20°. The speed ratio is 0.8 and the diameter of the rotor blades is 1 meter. Determine the power developed if the mass flow rate of steam is 0.785 kg per second.
a) 6.534 kW
b) 7.654 kW
c) 8.425 kW
d) 9.612 kW
View Answer
Explanation: Given, N = 1500 r.p.m., α = 20°, ρ = 0.8, D = 1 m, ṁ = 0.785 kg/s
Cbl = \(\frac{π*D*N}{60} = \frac{π*1*1500}{60}\) = 78.54 m/s
We know that,
ρ = \(\frac{C_{bl}}{C_1} \)
0.8 = \(\frac{78.54}{C_1} \)
C1 = 78.54/0.8 = 98.18 m/s
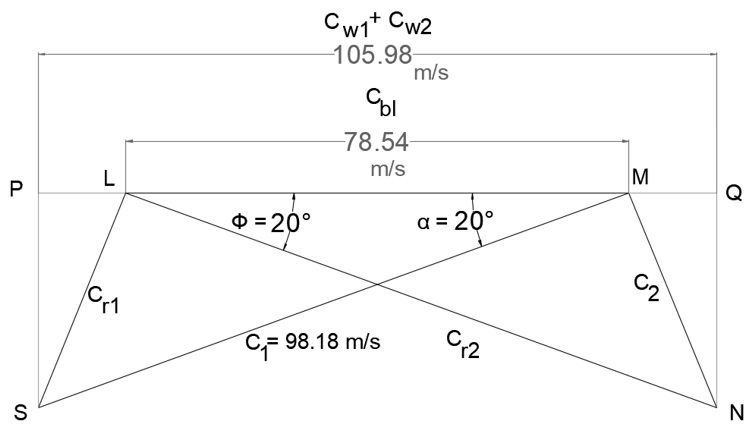
Steps of Construction:
Select a suitable scale and draw a line LM to represent Cbl (= 78.54 m/s).
At point M, at an angle of 20° (α), cut a length MS to represent the velocity C1 (= 98.18 m/s). Join LS. Produce L to meet the perpendicular drawn from S at P. Thus inlet triangle is completed.
For a Parson’s turbine:
Cr2 = C1 = 98.18 m/s
and Ф = α = 20°
At L, at an angle of 20° (Ф), cut a length LN to represent Cr2 (= 98.18 m/s). Join MN.
Produce M to meet the perpendicular drawn from N at Q. Thus outlet triangle is completed.
By measurement:
Cw1 + Cw2 = 105.98 m/s
Power Developed = ṁ(C_w1+C_w2 )*C_bl = 0.785(105.98)*78.54 = 6534.08 W or 6.534 kW.
8. In a steam turbine the turbine blade’s tip experiences more erosion than any other part.
a) True
b) False
View Answer
Explanation: In case of high and intermediate pressure turbines, the intermediate pressure stages’ steam is wet, which results in the corrosion and erosion of turbine blades. Also turbine blades are subjected to high centrifugal stresses. The effect of moisture is most eminent when it exceeds 10 per cent. Centrifugal force results in concentration of water particles in the outer annulus and the tip speed is greater than the root speed, hence tip experiences more erosion than any other part.
9. Which of the following is the correct expression to calculate stage efficiency in steam turbines?
a) \(\frac{Heat \, converted \, into \, useful \, work}{Adiabatic \, heat \, drop \, per \, stage}\)
b) \(\frac{Net \, work \, done \, on \, shaft \, per \, stage \, per \, kg \, of \, steam}{Adiabatic \, heat \, drop \, per \, stage}\)
c) \(\frac{Heat \, converted \, into \, useful \, work}{Total \, adiabatic \, heat \, drop}\)
d) \(\frac{Net \, work \, done \, on \, shaft \, per \, stage \, per \, kg \, of \, steam}{Total \, adiabatic \, heat \, drop}\)
View Answer
Explanation: Stage efficiency gives the idea of loses in one stage only. It covers all kind of losses in the stage including losses in nozzles, diaphragms, blades and discs.
Therefore, the correct answer is –
ηstage =\(\frac{Net \, work \, done \, on \, shaft \, per \, stage \, per \, kg \, of \, steam}{Adiabatic \, heat \, drop \, per \, stage}\)
10. Which of the following is the correct expression for internal efficiency in steam turbines?
a) \(\frac{Heat \, converted \, into \, useful \, work}{Total \, adiabatic \, heat \, drop}\)
b) \(\frac{Net \, work \, done \, on \, shaft \, per \, stage \, per \, kg \, of \, steam}{Adiabatic \, heat \, drop \, per \, stage}\)
c) \(\frac{Net \, work \, done \, on \, shaft \, per \, stage \, per \, kg \, of \, steam}{Total \, adiabatic \, heat \, drop}\)
d) \(\frac{Heat \, converted \, into \, useful \, work}{Net \, work \, done \, on \, shaft \, per \, stage \, per \, kg \, of \, steam}\)
View Answer
Explanation: Internal efficiency similar to stage efficiency, but unlike stage efficiency it covers the whole turbine.
The expression for internal efficiency is –
ηinternal = \(\frac{Heat \, converted \, into \, useful \, work}{Total \, adiabatic \, heat \, drop}\)
11. Which of the following is the correct formula for overall turbine efficiency in steam turbines?
a) \(\frac{Work \, delivered \, at \, the \, turbine \, cooupling \, in \, heat \, units \, per \, kg \, of vsteam}{Total \, adiabatic \, heat \, drop}\)
b) \(\frac{Work delivered \, at \, the \, turbine \, cooupling \, in \, heat \, units \, per \, kg \, of \, steam}{Adiabatic \, heat \, drop \, per \, stage}\)
c) \(\frac{Thermal \, efficiency \, on \, a \, Rankine \, cycle}{Brake \, thernal \, efficieny}\)
d) \(\frac{Heat \, converted \, into \, useful \, work}{Adiabatic \, heat \, drop \, per \, stage}\)
View Answer
Explanation: Overall turbine efficiency covers all kind of internal and external losses such as, leakage, radiation, bearing friction etc.
The expression for overall turbine efficiency is –
ηoverall = \(\frac{Work \, delivered \, at \, the \, turbine \, cooupling \, in \, heat \, units \, per \, kg \, of vsteam}{Total \, adiabatic \, heat \, drop}\)
12. Which of the following is the correct expression for net efficiency in steam turbines?
a) \(\frac{Brake \, thermal \, efficiency}{Thermal \, efficiency \, on \, the \, Rankine \, cycle}\)
b) \(\frac{Brake \, thermal \, efficiency}{Thermal \, efficiency \, on \, the \, Carnot \, cycle}\)
c) \(\frac{Thermal \, efficiency \, on \, the \, Rankine \, cycle}{Brake \, thermal \, efficiency}\)
d) \(\frac{Thermal \, efficiency \, on \, the \, Carnot \, cycle}{Brake \, thermal \, efficiency}\)
View Answer
Explanation: Net efficiency is also called as efficiency ratio. It is the ratio of brake thermal efficiency to thermal efficiency on the Rankine cycle.
Therefore,
ηnet = \(\frac{Brake \, thermal \, efficiency}{Thermal \, efficiency \, on \, the \, Rankine \, cycle}\)
13. Which of the following is the correct definition for ‘Adiabatic Power’?
a) It is the power developed at the rim
b) It is the actual power transmitted by the turbine
c) It is the power based on the total internal steam flow and adiabatic heat drop
d) It is the power developed by the blades
View Answer
Explanation: Adiabatic power is based on the total internal steam flow and adiabatic heat drop. Adiabatic power is calculated assuming that the expansion of the steam is isentropic or adiabatic.
Adiabatic power = ṁ * (isentropic enthalpy drop).
14. Which of the following is the correct definition of ‘Shaft Power’?
a) It is the power developed by the blades
b) It is the power developed at the rim
c) It is the power based on the total internal steam flow and adiabatic heat drop
d) It is the actual power transmitted by the turbine
View Answer
Explanation: Shaft power is the actual power transmitted by the turbine. Shaft power takes all possible types of power losses into account including, reheating due to friction, nozzle losses, blade friction, pressure variation through channels etc.
15. Which of the following statements regarding a Reaction turbine is FLASE?
a) The relative velocity of steam with respect to moving blade increases as the steam glides over the turbine blade
b) The degree of reaction for a reaction turbine is defined as the ratio of heat drop in moving blade to heat drop in the stage
c) If the degree of reaction of a reaction turbine is 50% then, the moving blade and the fixed blades have the same shape
d) The angles of receiving tips of fixed and moving blades are always equal
View Answer
Explanation: In a reaction turbine, the angles of receiving tips of moving and fixed blades are not necessarily equal. They are equal in case of Parson’s reaction turbine, which is a special case of reaction tubines. In Parson’s reaction turbine the shape of moving and fixed blades is same and degree of reaction is 50%.
Sanfoundry Global Education & Learning Series – Thermal Engineering
To practice all areas of Thermal Engineering, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Practice Chemical Engineering MCQs
- Check Mechanical Engineering Books
- Apply for Chemical Engineering Internship
- Check Chemical Engineering Books
- Apply for Mechanical Engineering Internship
