This set of Thermal Engineering Multiple Choice Questions & Answers (MCQs) focuses on “Reciprocating Compressor”.
1. What is the range of pressure ratio in case of compressors?
a) Always equals to 1
b) Always less than 1
c) Always greater than 1
d) Always less than 0
View Answer
Explanation: Pressure ratio is defined as the ratio of exit pressure to the inlet pressure. Since, the discharge (exit) pressure is always greater than the inlet pressure; the value of pressure ratio is always greater than 1.
2. Which of the following is the unit of compressor capacity?
a) Meter
b) Meter2
c) Meter3
d) Meter3/second
View Answer
Explanation: Compressor capacity is defined as the volume of air delivered by the compressor per unit time. It is expressed in “meter3/second”, “meter3/minute”, “liter3/second”, and “liter3/minute”.
3. In how many revolutions of the crankshaft, a single-acting reciprocating compressor completes one cycle?
a) One revolution
b) Two revolutions
c) Three revolutions
d) Four revolutions
View Answer
Explanation: During suction stroke, piston moves from top dead center (TDC) to bottom dead center (BDC) and crankshaft completes half-revolution. Then, during compression stroke, the piston moves from BDC to TDC, and the crankshaft completes another half-revolution, thus completing one complete revolution.
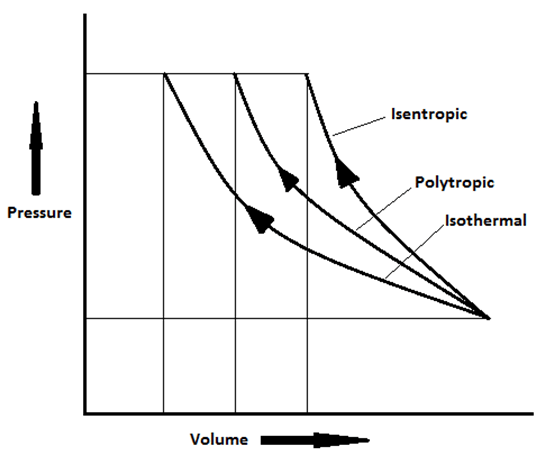
4. Which of the following comparisons holds true for the work required by the compressor during various compression processes?
a) Isothermal < Polytropic < Isentropic
b) Isothermal > Polytropic > Isentropic
c) Polytropic < Isentropic < Isothermal
d) Polytropic > Isentropic > Isothermal
View Answer
Explanation: From the pressure vs. volume diagram, it can be seen that the work done on the air is minimum when the compression is isothermal. The work done is maximum when the compression is isentropic, because isothermal line has lower slope than isentropic line.
5. Which of the following statements is incorrect with respect to reciprocating compressors?
a) Delivery of air is continuous
b) Delivery pressure is high
c) Pressure ratio is high
d) Flow rate of air is low
View Answer
Explanation: In reciprocating compressors in between a cycle there are two different processes, the suction, and the compression stroke. During the suction stroke, the suction valve is open and the delivery valve is closed. During compression, the suction valve is closed and the delivery valve is open for the compressed air to be delivered. Hence, only for half of the time the delivery of air occurs in a cycle, and that’s why delivery of compressed air is intermittent, i.e., discontinuous.
6. A single acting reciprocating compressor compresses 5kg of air from 1bar to 7bar. The initial temperature is 15°C. Calculate the work required if the compression process follows the law PV1.2 = Constant.
a) W = 150KJ
b) W = 288KJ
c) W = 205.42KJ
d) W = 949.93KJ
View Answer
Explanation:
Given: m = 5kg; P1 = 1bar; P2 = 7bar; T1 = 15°C = 15 + 273 = 288K; n = 1.2;
We know that work required by the compressor in polytropic process is given by,
W = \(\frac{n}{n-1}\) × mRT1 \(\bigg\{(\frac{P_2}{P_1})^{\frac{n-1}{n}}-1\bigg\}\)
Substituting the values in the above equation,
W = \(\frac{1.2}{1.2-1}\) × 5 × 287 × 288 \(\bigg\{(\frac{7}{1})^{\frac{1.2-1}{1.2}}-1\bigg\}\)
W = \(\frac{1.2}{1.2-1}\) × 413280 × {1.383 – 1}
We get, W = 949.93KJ.
7. Which of the following statements is incorrect related to multistage compression in reciprocating compressors?
a) Improves volumetric efficiency for the given pressure ratio
b) Reduces the leakage loss considerably
c) Reduces the cost of compressor
d) Temperature of air, at the end of compression, is too high
View Answer
Explanation: At the end of compression, the temperature of air is too high in single-stage compression. It may heat the cylinder head or it may burn the lubricating oil. In the multistage compression process, there is effective lubrication because of the lower temperature range.
8. Which of the following is the condition for which the required compressor work is minimum in a multistage compression process under perfect intercooling? Where P1 is the intake pressure, P2 is the intercooler pressure and P3 is the delivery pressure.
a) P2 = \(\sqrt{P_1 P_3}\)
b) P2 = P1 + P3
c) P2 = P3 / P1
d) P2 = P3 – P1
View Answer
Explanation: The minimum value of the intermediate or intercooler pressure is given by P2 = \(\sqrt{P_1 P_3}\) when the intake pressure P1 and the delivery pressure P3 are fixed. The obtained value of P2 denotes the pressure of the intercooler at which the work required to drive the compressor is minimum.
9. Which of the following is the correct value of intermediate pressure for minimum work required by the multistage compressor, with perfect intercooling to compress 1kg of air from 1bar to 25bar?
a) 4bar
b) 12bar
c) 15bar
d) 5bar
View Answer
Explanation:
Given: P1 = 1bar; P3 = 25bar
We know that the pressure of the intercooler at which the work required to drive the compressor is minimum is given by P2 = \(\sqrt{P_1 P_3}\) Substituting the given values, P2 = \(\sqrt{1 × 25}\) = 5bar.
10. Which of the following is the correct formula for the volumetric efficiency of a reciprocating compressor?
a) ηvol = 1 + C – C(P2 / P1)1/n
b) ηvol = 1 – C + C(P2 / P1)1/n
c) ηvol = 1 + C + C(P2 / P1)1/n
d) ηvol = 1 – C – C(P2 / P1)1/n
View Answer
Explanation:
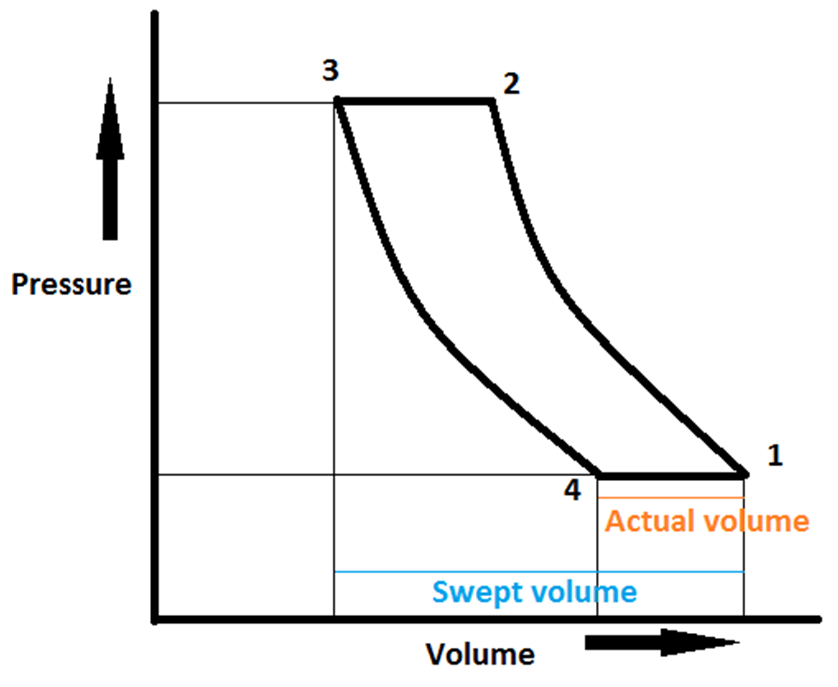
We know that volumetric efficiency is given by;
ηvol = \(\frac{V_{act}}{V_{swept}} = \bigg(\frac{V_1-V_4}{V_{swept}}\bigg) = \bigg(\frac{V_{swept}-(V_4-V_3)}{V_{swept}}\bigg)\)
ηvol = 1 – \(\frac{V_{clearance}}{V_{swept}}\bigg(\frac{V_4}{V_{clearance}} -1\bigg)\)
∵ Clearance ratio “C” = \(\frac{V_{clearance}}{V_{swept}}\)
∴ηvol = 1 – C\(\bigg(\frac{V_4}{V_{clearance}} – 1\bigg)\)
Also, we know that the process 3 to 4 is a polytropic process;
So, \(\frac{V_4}{V_3}\) = \((\frac{P_2}{P_1})^{\frac{1}{n}}\)
Therefore, ηvol = 1 – C\(\bigg((\frac{P_2}{P_1})^{\frac{1}{n}} – 1\bigg)\)
or ηvol = 1 + C – C\((\frac{P_2}{P_1})^{\frac{1}{n}}\)
Sanfoundry Global Education & Learning Series – Thermal Engineering
To practice all areas of Thermal Engineering, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Check Thermal Engineering Books
- Practice Mechanical Engineering MCQs
- Check Mechanical Engineering Books
- Check Chemical Engineering Books
- Apply for Chemical Engineering Internship
