Thermal Engineering Questions and Answers – Reaction Turbines – 1

This set of Thermal Engineering Multiple Choice Questions & Answers (MCQs) focuses on “Reaction Turbines – 1”.

1. The magnitude of velocity of steam relative to moving blade in case of an impulse turbine _____
a) always remains constant as steam glides over the blades
b) depending on friction present on the blades, increases or remains constant as the steam glides over the blades
c) depending on friction present on the blades, decreases or remains constant as the steam glides over the blades
d) depending on friction present on the blades, increases or decreases as the steam glides over the blades
View Answer

2. In case of reaction turbines, the magnitude of velocity of steam relative to moving blade increases as the steam progresses.
a) True
b) False
View Answer

3. Which of the following expressions for degree of reaction (R_d) of a reaction turbine stage is correct?
a) R_d=\(\frac{Heat \, drop \, in \, moving \, blades}{Heat \, drop \, in \, the \, stage}\)
b) R_d=\(\frac{Heat \, drop \, in \, the \, stage}{Heat \, drop \, in \, moving \, blades}\)
c) R_d=\(\frac{Heat \, drop \, in \, fixed \, blades}{Heat \, drop \, in \, the \, stage}\)
d) R_d=\(\frac{Heat \, drop \, in \, the \, stage}{Heat \, drop \, in \, fixed \, blades}\)
View Answer

4. Which of the following is the correct formula for calculating the degree of reaction of a reaction turbine?
a) R_d=\(\frac{2C_{bl}(C_{w1}+C_{w2})}{C_{r2}^2-C_{r1}^2} \)
b) R_d=\(\frac{C_{r2}^2-C_{r1}^2}{2C_{bl} (C_{w1}+C_{w2})} \)
c) R_d=\(\frac{C_{bl}(C_{w1}+C_{w2})}{2(C_{r2}^2-C_{r1}^2)} \)
d) R_d=\(\frac{2(C_{r2}^2-C_{r1}^2)}{C_{bl}(C_{w1}+C_{w2})} \)
View Answer

5. The degree of reaction of a Parson’s reaction turbine is _____
a) 0%
b) 25%
c) 50%
d) 100%
View Answer

6. Which of the following statements does NOT hold true for a Parson’s reaction turbine?
a) α = Ф
b) θ = β
c) C₁ = C_r2
d) C_r1 = C_r2
View Answer

7. What should be the ratio of blade speed to absolute velocity of steam leaving the nozzle for a Parson’s reaction turbine to work at maximum efficiency?
a) cos⁡α
b) cos⁡β
c) sin⁡α
d) sin⁡β
View Answer

8. The maximum value of efficiency for a Parson’s reaction turbine is _____
a) \(\frac{2(cos⁡)^2}{1+(cos ⁡α)^2} \)
b) \(\frac{2(cos α)^2}{1+(cos ⁡α)^2} \)
c) \(\frac{1+(cos ⁡α)^2}{2(cos α)^2} \)
d) \(\frac{2(cos α)^2}{1+(cos ⁡α)^2} \)
View Answer

9. Which of the following velocity diagram ccorresponds to a Parson’s reaction turbine?
a)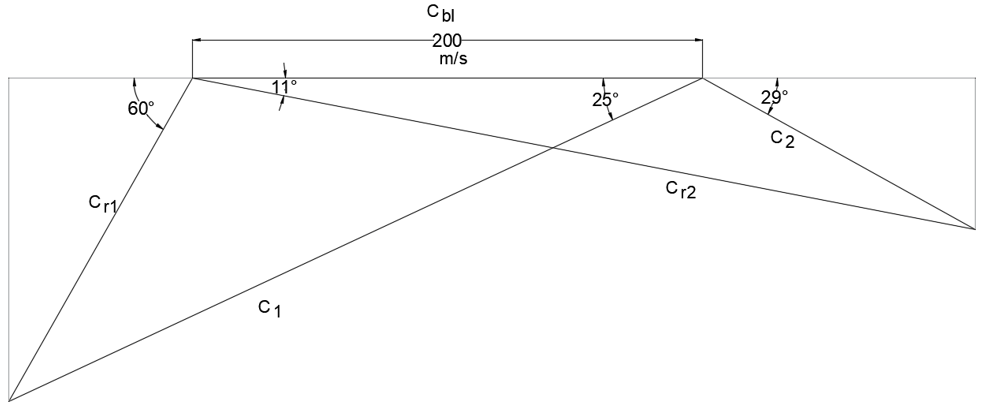
b)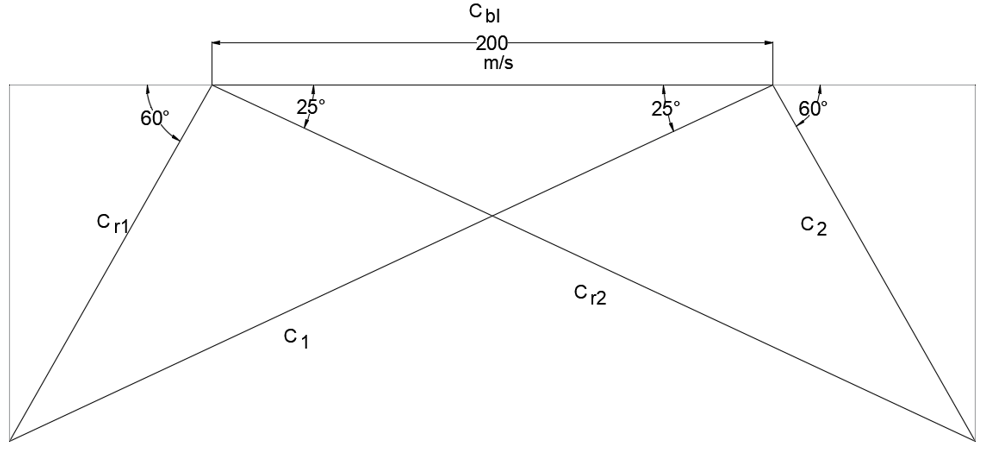
c)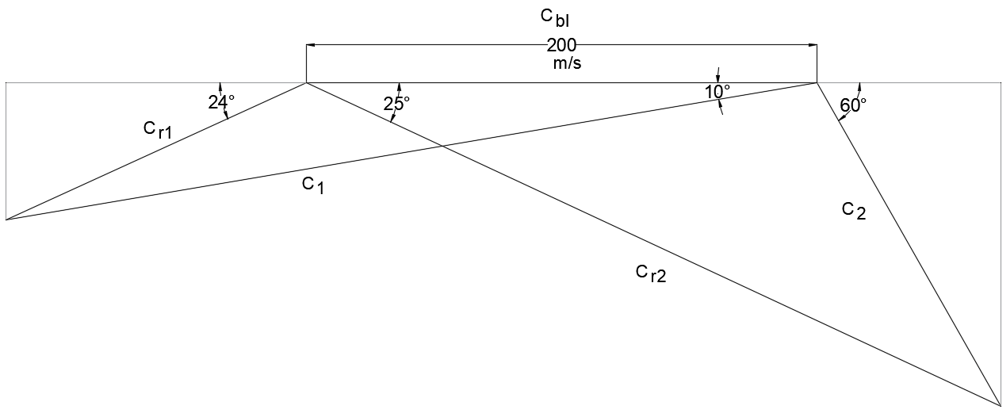
d)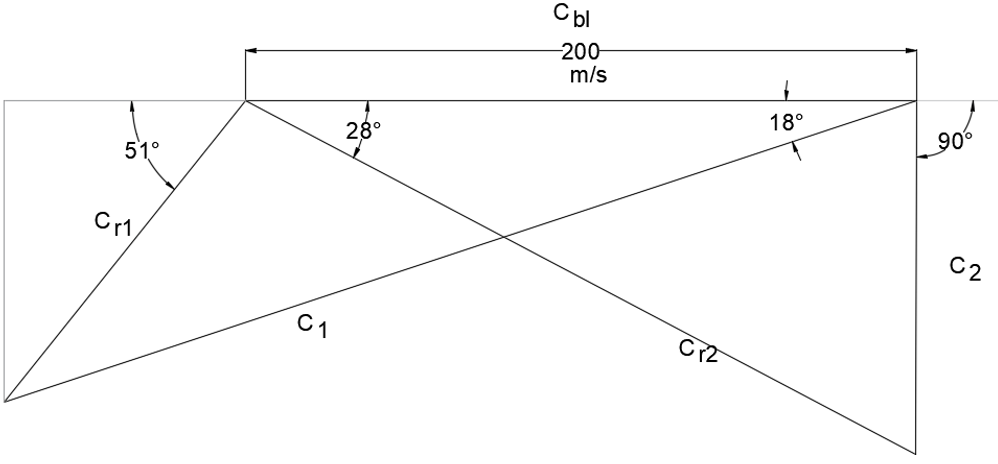
View Answer

Answer: b
Explanation: Parson’s reaction turbine has symmetrical moving and fixed blades which results in a symmetrical velocity diagram. The following properties are observed in a velocity diagram of a Parson’s reaction turbine.
θ = β and α = Ф,
C₁ = C_r2and C₂ = C_r1
Therefore, the correct answer is

10. The axial force on the blades in Parson’s reaction turbine is always zero.
a) True
b) False
View Answer

11. The following data refers to a particular stage of a Parson’s reaction turbine:
Mean blade speed = 90 m/s
Velocity of steam leaving the nozzle = 120 m/s
Nozzle angle = 20°
Mass flow rate of steam = 0.8 kg per second
Calculate the tangential force on the blade.
a) 203.54 N
b) 108.42 N
c) 65.32 N
d) 195.45 N
View Answer

Answer: b
Explanation: C_bl= 90 m/s, α = 20°, C₁ = 120 m/s, ṁ = 0.8 kg/s

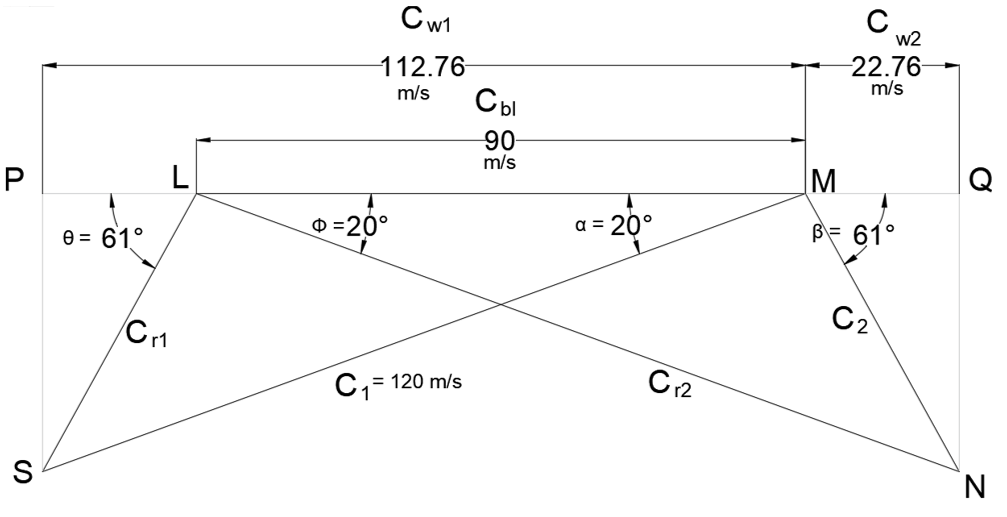
Steps of Construction:
Select a suitable scale and draw a line LM to represent C_bl (=90 m/s).
At point M, at an angle of 20° (α), cut a length MS to represent the velocity C₁ (=120 m/s). Join LS. Produce L to meet the perpendicular drawn from S at P. Thus inlet triangle is completed.
For a Parson’s turbine:
Ф = α = 20°
and C_r2=C₁ = 120 m/s
At L, at an angle of 20° (Ф), cut a length LN to represent C_r2(=120 m/s). Join MN.
Produce M to meet the perpendicular drawn from N at Q. Thus outlet triangle is completed.
By measurement:
C_w1 = 112.76 m/s and C_w2 = 22.76 m/s
Tangential force = ṁ(C_w1 + C_w2) = 0.8(112.76 + 22.76) = 108.42 N.

12. In a single stage Parson’s reaction turbine, the mean blade velocity is observed to be 60 m/s and the nozzle angle to be 20°. Determine the the entrance angle of moving blade if the absolute velocity of the steam leaving the nozzle is 120 m/s.
a) 38°
b) 56°
c) 23°
d) 28°
View Answer

Answer: a
Explanation: C_bl = 60 m/s, α = 20°, C₁ = 120 m/s

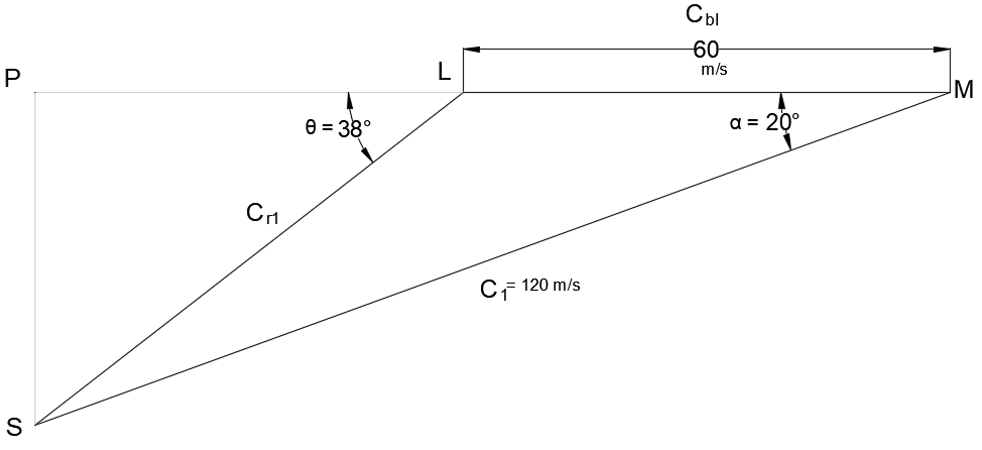
Steps of Construction:
Select a suitable scale and draw a line LM to represent C_bl (=60 m/s).
At point M, at an angle of 20° (α), cut a length MS to represent the velocity C₁ (=120 m/s). Join LS. Produce L to meet the perpendicular drawn from S at P. Thus inlet triangle is completed.
By measurement:
θ = 38°.

13. In a reaction turbine, the fixed blades and the moving blades are of the same shape but reversed in direction. The mean blade speed is 30 m/s. The absolute velocity of the steam leaving the nozzle is 90 m/s and the absolute velocity of steam leaving the moving blade is 64 m/s. Determine the nozzle angle.
a) 20°
b) 25°
c) 30°
d) 35°
View Answer

Answer: b
Explanation: Given, C_bl = 30 m/s, C₀ = C_r1 = 64 m/s, C₁ = 90 m/s

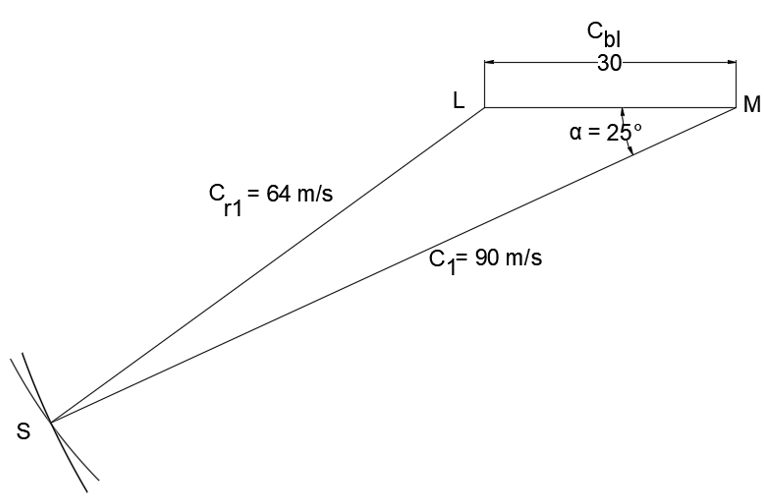
Steps of Construction:
Select a suitable scale and draw a line LM to represent C_bl (= 30 m/s).
At point M, draw an arc of length corresponding to C₁ (90 m/s). At point L, draw an arc of length corresponding to length 64 m/s, cutting the previous arc at S. The inlet triangle is complete.
By measurement:
α = ∠LMS = 25°.

14. In a Parson’s reaction turbine, the outlet angle of blade is 25°. Calculate the work done per second by the blades if the blade mean blade speed is 60 m/s and the absolute velocity of the steam leaving the nozzle is 120 m/s. The mass flow rate of steam is 0.1 kg per second.
a) 756 W
b) 854 W
c) 945.12 W
d) 1065 W
View Answer

Answer: c
Explanation: Given, α = Ф = 25°, C_bl = 60 m/s, C₁ = 120 m/s, ṁ = 0.1 kg/s

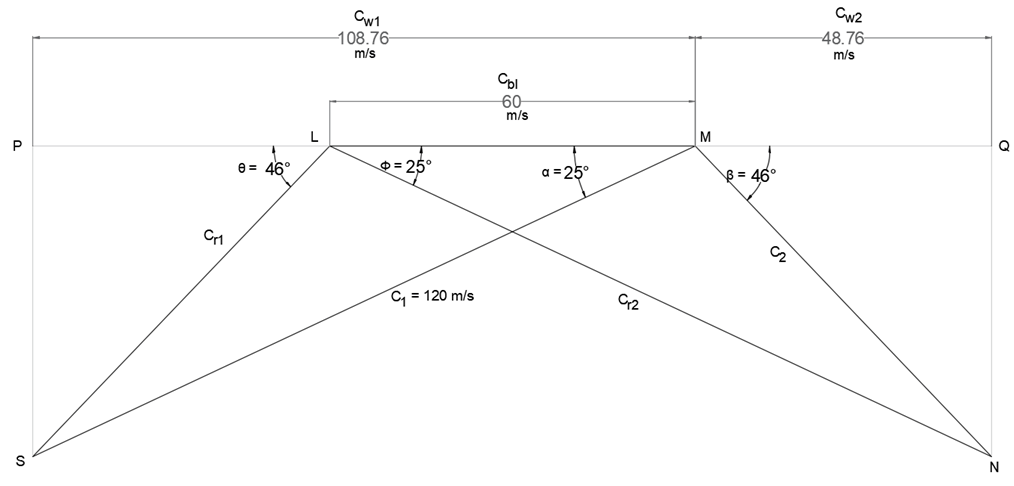
Steps of Construction:
Select a suitable scale and draw a line LM to represent C_bl (= 60 m/s).
At point M, at an angle of 25° (α), cut a length MS to represent the velocity C₁ (= 120 m/s). Join LS. Produce L to meet the perpendicular drawn from S at P. Thus inlet triangle is completed.
For a Parson’s turbine:
Ф = α = 25°
and C_r2= C1 = 120 m/s
At L, at an angle of 25° (Ф), cut a length LN to represent C_r2(= 120 m/s). Join MN.
Produce M to meet the perpendicular drawn from N at Q. Thus outlet triangle is completed.
By measurement:
C_w1 = 108.76 m/s and C_w2 = 48.76 m/s
Work done per second = ṁ (C_w1 + C_w2) C_bl = 0.1 (108.76 + 48.76) 60 = 945.12 W.

15. In a single stage reaction turbine, the mean blade velocity is observed to be 200 m/s and the nozzle angle is 20°. The absolute value of the steam leaving the nozzle is 350 m/s. The factor with which the relative velocity of steam changes wit respect to the moving is 2.1. If the moving blade inlet and outlet aangles are equal then calculate the degree of reaction of the turbine.
a) 50%
b) 66%
c) 75%
d) 84%
View Answer

Answer: b
Explanation: Given, C_bl = 200 m/s, α = 20°, C₁ = 350 m/s, K = 2.1, θ = Ф

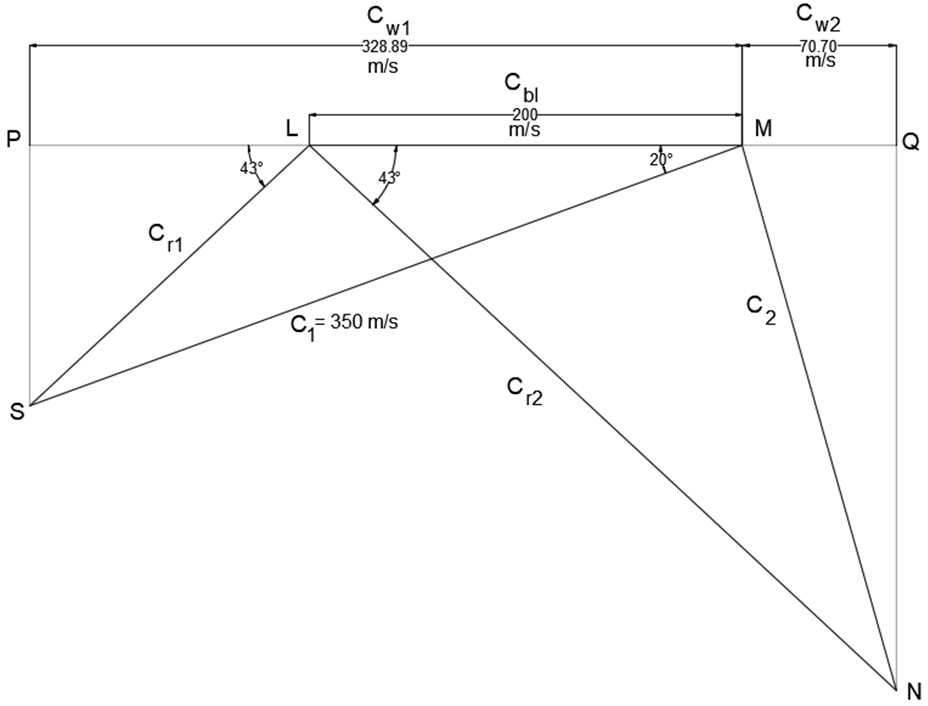
Steps of Construction:
Select a suitable scale and draw a line LM to represent C_bl (= 200 m/s).
At point M, at an angle of 20° (α), cut a length MS to represent the velocity C₁ (= 350 m/s). Join LS. Produce L to meet the perpendicular drawn from S at P. Thus inlet triangle is completed.
By measurement:
θ = 43° and C_r1 = 175.91 m/s
It Is givne that, Ф = θ = 43° and C_r2= KC_r1 = 2.1 (175.91) = 369.41 m/s
At L, at an angle of 43° (Ф), cut a length LN to represent C_r2(= 369.41 m/s). Join MN.
Produce M to meet the perpendicular drawn from N at Q. Thus outlet triangle is completed.
By measurement:
C_w1 = 328.89 m/s and C_w2 = 70.70 m/s
Degree of Reaction, R_d=\(\frac{C_{r2}^2-C_{r1}^2}{2C_{bl}(C_{w1}+C_{w2})} = \frac{369.41^2-175.91^2}{2*200(328.89+70.70)}\) = 0.66 or 66%.

Sanfoundry Global Education & Learning Series – Thermal Engineering

To practice all areas of Thermal Engineering, here is complete set of 1000+ Multiple Choice Questions and Answers.

If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]