Thermal Engineering Questions and Answers – Impulse Turbines – 2

This set of Thermal Engineering MCQs focuses on “Impulse Turbines – 2”.

1. In a simple impulse turbine, it is observed that 22.4 kJ energy is lost to blade friction. The uses steam at a rate of 1 kg/s. If the velocity of steam relative to the moving blade at an entrance is 300 m/s, determine the blade velocity coefficient.
a) 0.325
b) 0.456
c) 0.867
d) 0.951
View Answer

2. The maximum possible efficiency of a De-laval turbine is 88.3%. Determine the nozzle angle.
a) 15°
b) 20°
c) 25°
d) 30°
View Answer

3. In a De laval turbine, steam leaves nozzle with a velocity of 1300 m/s. The nozzle angle is 25° and the mean blade speed is 500 m/s. The inlet and outlet blade angles are equal. Find out work done per kg of steam if the blades of the turbine are frictionless.
a) 678.205 kJ
b) 798.562 kJ
c) 365.458 kJ
d) 456.321 kJ
View Answer

Answer: a
Explanation: C₁ = 1300 m/s, α = 25°, C_bl = 500 m/s, θ = Ф

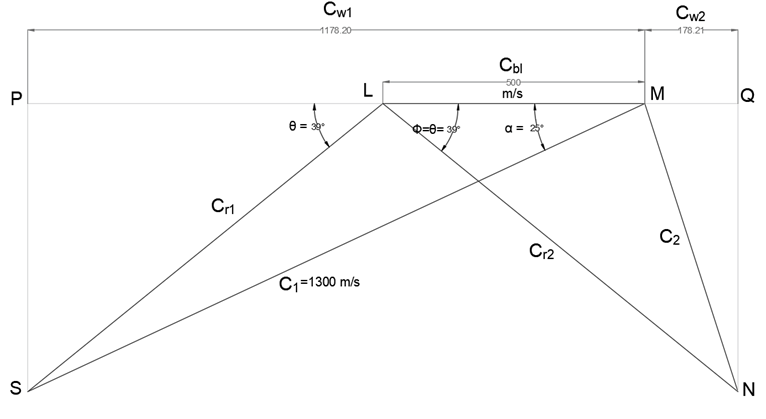
Steps for Construction –
Select a suitable scale and draw line LM corresponding to 500 m/s (C_bl).
At M, cut a length at S corresponding to 1300 m/s (C₁) at an angle of 25° (α). Join LS.
Produce L to meet perpendicular from S at P. The inlet triangle is complete.
By measurement –
C_r1 = 872.81 m/s, θ = 39°
Since the blades of the turbine are considered to be frictionless
C_r2=C_r1 = 872.81 m/s
Also, Ф = θ = 39°
At L, cut a length at N corresponding to 872.81 m/s (C_r2) at an angle of 39°. Join MN.
Produce M to meet perpendicular from N at Q. The outlet triangle is complete.
By measurement –
C_w1 = 1178.20 m/s and C_w2 = 178.21 m/s
Work done per kg of steam = (C_w1 + C_w2)*C_bl = (1178.20 + 178.21)*500 = 678205 J or 678.205 kJ.

4. In a De-Laval turbine, steam with absolute velocity of 950 m/s is supplied through a nozzle. The mean blade velocity is 300 m/s. If the turbine is working at its maximum possible efficiency, determine the work done per kg of steam.
a) 180 kJ
b) 200 kJ
c) 1705 kJ
d) 1805 kJ
View Answer

5. In a single row impulse turbine, the absolute velocity of steam leaving the turbine is 900 m/s. The nozzle angel is 20°. The mean blade speed is 300 m/s. The inlet blade angle is equal to the outlet blade angle. Determine the angle made by the discharging steam with the tangent of the wheel at the exit of moving blade. Neglect friction on turbine blades.
a) 27°
b) 36°
c) 51°
d) 90°
View Answer

Answer: c
Explanation: C₁ = 900 m/s, α = 20°, C_bl = 300, θ = Ф, K = 1

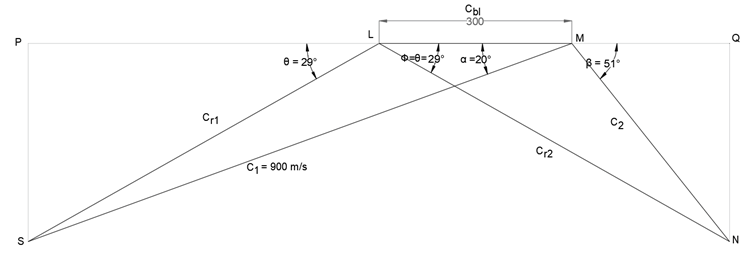
Steps for construction –
Select a suitable scale and draw line LM corresponding to 300 m/s (C_bl).
At M, at an angle of 20° cut a length corresponding to 900 m/s at S. Join LS.
Produce L to meet perpendicular from S at P. The inlet triangle is complete.
By measurement –
C_r1 = 626.55 m/s, θ = 29°
Since the blades of the turbine are considered to be frictionless
C_r2 = C_r1 = 626.55 m/s
Also, Ф = θ = 29°
At L, cut a length at N corresponding to 626.55 m/s (C_r2) at an angle of 29°. Join MN.
Produce M to meet perpendicular from N at Q. The outlet triangle is complete.
By measurement, β = 51°.

6. In a single row impulse turbine, steam leaves the nozzle at 600 m/s. The nozzle angle and the mean blade speed is 25° and 200 m/s. The blade velocity coefficient is 0.8. Determine the blade outlet angle if the steam leaves the turbine blades axially.
a) 54°
b) 60°
c) 66°
d) 74°
View Answer

Answer: a
Explanation: C₁ = 600 m/s, α = 25°, C_bl = 200 m/s, K = 0.8, β = 90°

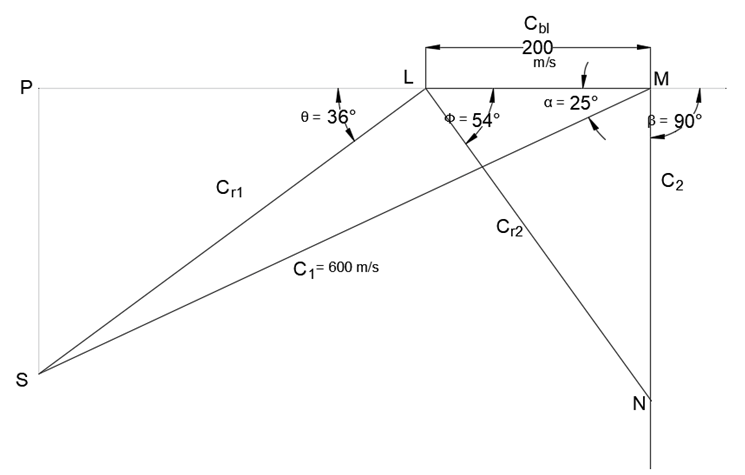
Steps for construction –
Select a suitable scale and draw line LM corresponding to 200 m/s (C_bl).
At M, at an angle of 25° cut a length corresponding to 600 m/s at S. Join LS.
Produce L to meet perpendicular from S at P. The inlet triangle is complete.
By measurement –
C_r1 = 427.18 m/s, θ = 36°
C_r2 = KC_r1 = 0.8(427.18) = 341.74 m/s
Through M, draw a ray perpendicular to LM.
Join L to a point N on ray through M such that the length LN should correspond to 341.74 m/s.
By measurement, Ф = 54°.

7. In a simple impulse turbine, steam leaves nozzle at 1200 m/s. The mean blade speed and nozzle angle is 300 m/s and 20° respectively. The inlet and outlet blade angles are equal. The blades of the turbine are frictionless. Determine the stage efficiency if the nozzle efficiency is 85%.
a) 58.65%
b) 62.32%
c) 75.45%
d) 84.37%
View Answer

Answer: a
Explanation: C₁ = 1200 m/s, C_bl = 300 m/s, α = 20°, θ = Ф, K=1, η_nozzle = 0.85

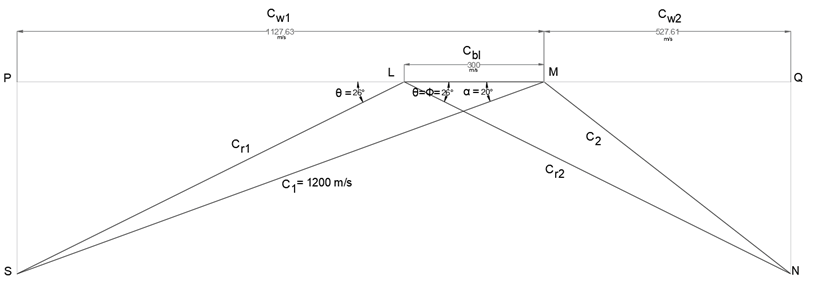
Steps for Construction –
Select a suitable scale and draw line segment LM corresponding to C_bl (300 m/s).
At M, at an angle of 20° (α), cut a length at S corresponding to C₁ (1200 m/s). Join LS.
Produce L to meet perpendicular from S at P. The inlet triangle is complete.
By measurement –
θ = 26°, C_r1 = 923.81 m/s
Since the turbine blades are frictionless,
C_r2= C_r1 = 923.81 m/s
Also, Ф = θ = 26°
At L, at an angle of 26° (Ф) cut a length at N corresponding to C_r2(923.81 m/s). Join MN.
Produce M to meet perpendicular from N at Q. The outlet triangle is complete.
By measurement –
C_w1 = 1127.63 m/s and C_w2 = 527.61 m/s
Blade efficiency, η_blade = \(\frac{2*C_{bl}(C_{w1}+C_{w2})}{C_1^2} = \frac{2*300*(1127.63+527.61)}{1200^2}\) = 0.69
Stage efficiency, η_stage = η_blade * η_nozzle = 0.69*0.85 = 0.5865 or 58.65%.

8. A simple impulse turbine has one ring of moving blades running at 400 m/s. The steam velocity leaving the nozzle is 1300 m/s. If the nozzle angle is 25°, determine the blade inlet angle.
a) 15°
b) 20°
c) 25°
d) 35°
View Answer

Answer: d
Explanation: C_bl = 400 m/s, C₁ = 1300 m/s, α = 25°

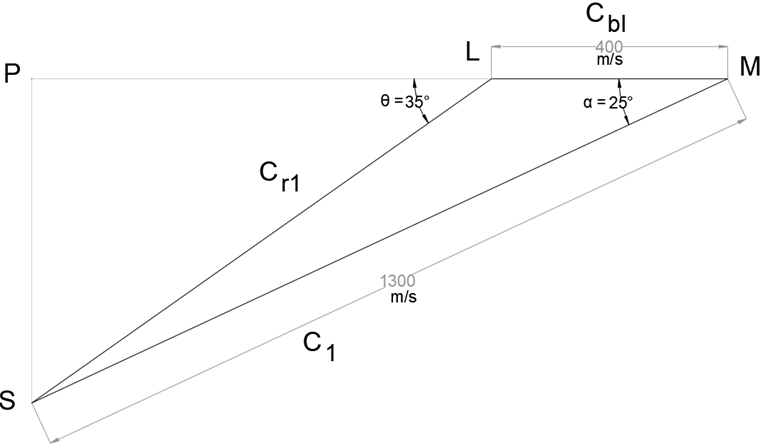
Steps for Construction-
Select a suitable scale and draw line segment LM corresponding to C_bl (400 m/s).
At M, at an angle of 25° (α), cut a length at S corresponding to C₁ (1300 m/s). Join LS.
Produce L to meet perpendicular from S at P. The inlet triangle is complete.
By measurement –
θ = 35°.

9. In a single stage impulse turbine nozzle angle is 20° and the mean blade speed is 300 m/s. Steam leaves the nozzle at a velocity of 700 m/s. Determine the exit velocity of the steam if the turbine blades are equiangular and frictionless.
a) 154.65 m/s
b) 195.65 m/s
c) 246.30 m/s
d) 321.32 m/s
View Answer

Answer: c
Explanation: C_bl = 300 m/s, C₁ = 700 m/s, α = 20°, θ = Ф, K=1

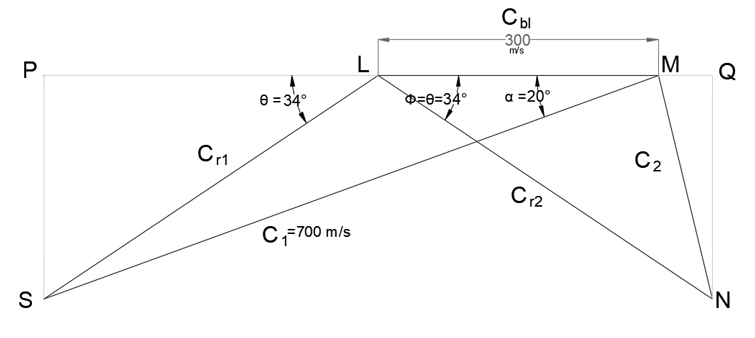
Steps for Construction –
Select a suitable scale and draw line segment LM corresponding to C_bl (300 m/s).
At M, at an angle of 20° (α), cut a length at S corresponding to C₁ (700 m/s). Join LS.
Produce L to meet perpendicular from S at P. The inlet triangle is complete.
By measurement –
θ = 34°, C_r1 = 430.50 m/s
Since the turbine blades are frictionless,
C_r2 = C_r1 = 430.50 m/s
Also, Ф = θ = 34°
At L, at an angle of 34° (Ф) cut a length at N corresponding to C_r2(430.50 m/s). Join MN.
Produce M to meet perpendicular from N at Q. The outlet triangle is complete.
By measurement –
C₂ = 246.30 m/s.

10. In a single stage impulse turbine, the exit velocity of the steam is 90 m/s at an angle of 45° from the tangential direction. The mean blade speed is 200 m/s. The blades are equiangular and velocity coefficient of the blades is 0.8. Determine the velocity of steam leaving the nozzles.
a) 472.32 m/s
b) 535.50 m/s
c) 624.84 m/s
d) 784.36 m/s
View Answer

Answer: b
Explanation: C₂ = 90 m/s, β = 45°, C_bl = 200 m/s, θ = Ф, K = 0.8

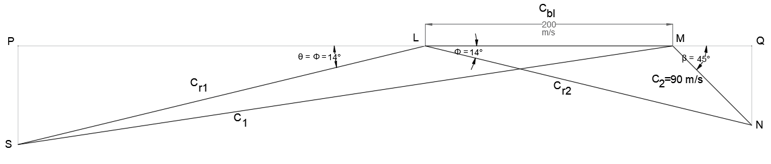
Steps for Construction-
Select a suitable scale and draw line segment LM corresponding to C_bl (200 m/s).
At M, at an angle of 45° (β) cut a length at N corresponding to C₂ (90 m/s). Join LN.
Produce M to meet perpendicular from N at Q. The outlet triangle is complete.
By measurement –
Ф = 14°, C_r2 = 271.22 m/s
C_r2=\(\frac{C_{r1}}{K} = \frac{271.22}{0.8}\) = 339.02 m/s
Also, θ = Ф = 14°
At L, at an angle of 14° (θ) cut a length at S corresponding to 339.02 m/s. Join MS.
Produce L to meet perpendicular from S at P. The inlet triangle is complete.
By measurement,
C₁ = 535.50 m/s.

11. Which of the following statement regarding work done in impulse turbines is TRUE, if the blade speed ratio is equal to zero?
a) Maximum possible work done takes place
b) Work done becomes zero
c) Nothing can be stated about work done
d) work done per kg of steam is equal to
View Answer

12. Which of the following statement about efficiency of impulse turbines is TRUE, when the blade speed ratio is made equal to half of cosine of the nozzle angle?
a) Efficiency is minimum and is equal to \(\frac{cos⁡α^2}{2} \)
b) Efficiency is maximum and is equal to \(\frac{cos⁡α^2}{2} \)
c) Efficiency is minimum and is equal to cos⁡ α²
d) Efficiency is maximum and is equal to cos⁡ α²
View Answer

13. Which of the following statement about the work done per kg of steam in impulse turbines is TRUE, when the blade speed ratio is equals \(\frac{cos⁡ α}{2}\)? (α is the nozzle angle)
a) Work done per kg of steam is maximum and is equal to 2C₁²
b) Work done per kg of steam is minimum and is equal to 2C₁²
c) Work done per kg of steam is maximum and is equal to 2C_bl²
d) Work done per kg of steam is minimum and is equal to 2C_bl²
View Answer

14. Work done per kg of steam in an impulse turbine when the blade speed ratio (ρ) is equal to one is _____
a) 0
b) C_bl²
c) 2C_bl²
d) 2C_bl(C_f1+C_f2)
View Answer

15. In an impulse turbine, the axial force on the blades is zero if _____
a) the whirl components of the inlet and outlet absolute velocities are equal
b) the flow components of the inlet and outlet absolute velocities are equal
c) the exit velocity of steam is axial
d) the flow and whirl component of inlet velocity are equal
View Answer

Sanfoundry Global Education & Learning Series – Thermal Engineering

To practice MCQs on all areas of Thermal Engineering, here is complete set of 1000+ Multiple Choice Questions and Answers.

If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]