This set of Advanced Pavement Design Questions and Answers focuses on “GI and Triaxial Method – 2”.
1. A higher value of the group index indicates a strong subgrade.
a) True
b) False
View Answer
Explanation: The group index value is based on the soil type and its physical properties. A higher value of the group index suggests that the soil is of low quality and hence the subgrade will be weak.
2. The triaxial method is based on which equation?
a) Boussinesq’s stress
b) Boussinesq’s displacement
c) Burmister’s stress
d) Burmister’s displacement
View Answer
Explanation: The subgrade soil is considered as a homogeneous elastic single layer. Boussinesq’s theory can be applied to the soil. in the triaxial method of design, the displacement equation by Boussinesq is made use of.
3. What indicates that the traffic is light traffic in case of group index design chart?
a) CVPD < 20
b) CVPD < 50
c) AADT < 20
d) AADT < 50
View Answer
Explanation: The traffic volume is considered, so CVPD i.e. commercial vehicles per day is taken into account. AADT is the annual average daily traffic and it is considered in the R-value method. For light traffic, the number of commercial vehicles per day must be < 50.
4. In the triaxial method, the equation for the thickness of the pavement can be obtained by bringing ______ term to one side.
a) p
b) z
c) a
d) E
View Answer
Explanation: The Boussinesq’s deflection equation is given by \(Δ=\frac{3pa^2}{2E(a^2+z^2)^{1∕2}}\) . In this equation, the term z represents depth at which deflection is to be found out. So, the terms in the equation are rearranged and the equation for z is formulated. By assuming that the pavement is incompressible, z can be taken as the thickness of the pavement.
5. Find the group index of the soil having the following details:
Percentage passing 0.074 mm sieve = 45%
Liquid limit = 40%
Plastic limit = 33%
a) 5
b) 1
c) 0
d) 2
View Answer
Explanation: The equation to find the group index is given by GI =0.2a+0.005ac+0.01bd.
where “a” represents the portion of material passing 0.074 mm sieve, greater than 35 but not exceeding 75% (represented as a whole number in the range 0-40),
“b” represents the portion of material passing 0.074 mm sieve, greater than 15 but not exceeding 35% (expressed as a whole number in the range 0-40),
“c” represents the liquid limit in excess of 40 but less than 60 (expressed as a whole number in the range 0-20),
“d” represents the plasticity index in excess of 10 but less than 30 (expressed as a whole number in the range 0-20)
Using the data from the question,
Plasticity index = liquid limit – plastic limit = 40 – 33 = 7
a=45-35=10
b=45-15=30
c=40-40=0
d=7-10=0 (whole number)
GI =0.2×10+0.005×10×0+0.01×30×0=2
6. The GI value can be calculated using group index charts.
a) True
b) False
View Answer
Explanation: There are two methods to find the group index of soil. It can be done either by using the group index charts or by using the equation. There are two charts and the sum of GI from both charts is taken as the final GI.
7. Find the group index of the soil having the following details using the graphical method.
Percentage passing 0.074 mm sieve = 55%
Liquid limit = 45%
Plastic limit = 31%
a) 6
b) 7
c) 5
d) 8
View Answer
Explanation: There are two graphs available to find the value of the group index, GI of soil. The sum of GI values from both the graphs is taken as the GI value. The GI values from both the graphs can be read using the group index chart provided by the Highway Research Board, USA. The calculation and interpretation of GI value from both the graphs is explained below using a sample plot of the actual chart showing the data pertaining to the question.
The graph on the upper right-side shows % passing No. 200 sieve vs plasticity index values. The plasticity index, PI is obtained as the difference of liquid limit and plastic limit, 45 – 31 = 14%. From the graph, for percentage passing No. 200 sieve as 55 and PI of 14%, the group index is 1.7.
The graph on the lower left side shows % passing No. 200 sieve vs liquid limit values. The percentage passing is 55 and liquid limit, LL is 45%, so the group index is 4.4.
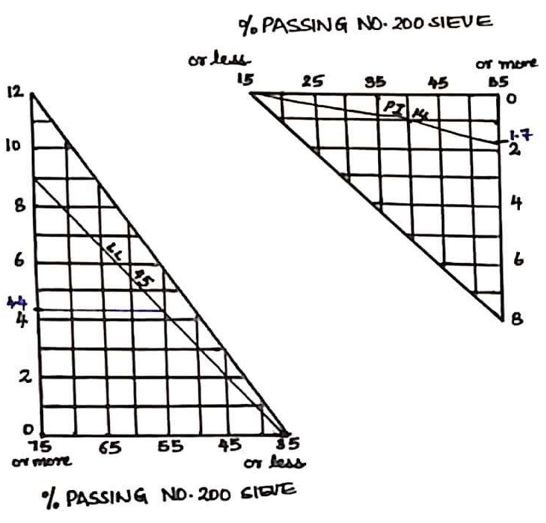
The GI values from both graphs are found to be 4.4 and 1.7. So, the GI = 4.4 + 1.7 = 6.1 ≈ 6
8. Find the thickness of pavement if the triaxial test is conducted on a sample and the data obtained are:
Wheel load, P = 4100 kg
Radius of contact area, a = 15 cm
Traffic coefficient, X = 1.5
Rainfall coefficient, Y = 0.7
Deflection, = 0.25 cm
Modulus of elasticity, E = 100 kg/cm2
a) 79.84 cm
b) 82.84 cm
c) 80.84 cm
d) 81.84 cm
View Answer
Explanation: The equation for finding the thickness of pavement using the triaxial method can be written as:
\(T=\sqrt{\left(\frac{3PXY}{2πEΔ}\right)^2-a^2}\)
Substituting the values from the question,
\(T=\sqrt{\left(\frac{3×4100×1.5×0.7}{2π×100×0.25}\right)^2-15^2}=80.84 cm\).
9. The parameters a, b, c and d for the group index computation are obtained as 23, 28, 10 and 12 respectively. The CVPD is found to be 450. Find the thickness of the surface and base of the pavement for the above details.
a) 29 cm
b) 39 cm
c) 30 cm
d) 20 cm
View Answer
Explanation: The group index can be calculated as GI =0.2a+0.005ac+0.01bd=0.2×23+0.005×23×10+0.01×28×12=9.11≈9. The traffic is 450 CVPD (≥300CVPD), so it comes under the heavy traffic condition. The design chart provided by the Highway Research Board, USA is used. A sample of the graph with the thickness of sub-base material represented by curve A and combined thickness of the surface, base and sub-base course represented by curve B for heavy traffic condition is shown below.
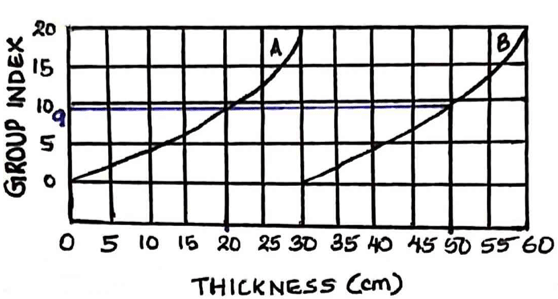
The group index value is 9 and it indicates poor subgrade. So, from the design chart, the thickness of sub-base material is taken and then the combined thickness is found out.
From the chart, the thickness of sub-base material (from curve A) = 20 cm
The combined thickness of surface, base and sub-base (from curve B) = 50 cm
Thickness of surface and base = 50 – 20 = 30 cm
10. What would be the thickness of pavement layers for a soil subjected to the triaxial test with the following data?
Wheel load, P = 4100 kg
Radius of contact area, a = 17 cm
Traffic coefficient, X = 8/6
Rainfall coefficient, Y = 0.8
Deflection, = 0.25 cm
Modulus of elasticity, Es = 100 kg/cm2
Modulus of elasticity of base course, Eb = 400 kg/cm2
Modulus of elasticity of 7 cm thick bituminous concrete surface course, Ebc = 1000 kg/cm2
a) 44.52 cm base course
b) 55.74 cm base course
c) 51.52 cm base course
d) 42.04 cm base course
View Answer
Explanation: The equation including the stiffness factor\(\left(\frac{E_s}{E_p}\right)^{1/3}\) is written as
T= \(\sqrt{(\frac{3PXY}{2\pi E_s\Delta})^2-a^2} x (\frac{E_s}{E_p})^{1/3}\)
Ep represents the modulus of elasticity of a pavement layer.
Finding the thickness of the base course,
T= \(\sqrt{(\frac{3×4100×8/6×0.8}{2π×100×0.25})^2-17^2} x (\frac{100}{400})^{1/3}=51.52 cm\)
51.52 cm is the total thickness of the base course. The thickness of the surface course is 7 cm and let it be equivalent to the thickness tb of the base course. So, the equivalent replacement tb for 51.52 cm with respect to the surface course of 7 cm can be obtained using the relation,
\( \frac{t_{bc}}{t_b} =(\frac{E_b}{E_{bc}} )^{1∕3}\)
\( t_b=t_{bc} (\frac{E_{bc}}{E_b })^{1∕3}=7×(\frac{1000}{400})^{1∕3}=9.5 cm\)
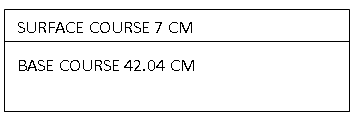
The required thickness of base course = 51.52 – 9.5 = 42.04 cm
The diagrammatic representation of the pavement layer is as below.
11. What is the lateral pressure applied to the soil in the triaxial test?
a) 1.4 kg/mm2
b) 1.4 kg/cm3
c) 1.4 kg/cm2
d) 1.4 kg/mm3
View Answer
Explanation: In order to find the values of modulus of elasticity of various materials, a lateral pressure of 1.4 kg/cm2 is applied on the soil subgrade. The value has been arbitrarily assumed by the Kansas State Highway Department, USA as the lateral confinement on their pavement layers.
Sanfoundry Global Education & Learning Series – Pavement Design.
To practice advanced questions and answers on all areas of Pavement Design, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Practice Civil Engineering MCQs
- Check Pavement Analysis and Design Books
- Check Civil Engineering Books
- Apply for Civil Engineering Internship
