This set of Engineering Physics Multiple Choice Questions & Answers (MCQs) focuses on “Fermi-Dirac Distribution”.
1. Fermi-Dirac statistics is for the ________
a) Distinguishable particles
b) Symmetrical Particles
c) Particles with half integral spin
d) Particles with integral spin
View Answer
Explanation: The Maxwell-Boltzmann statistics is for the distinguishable particles, which are basically the classical particles like atoms and molecules.
2. The difference between fermions and bosons is that bosons do not obey ______
a) Aufbau principle
b) Pauli’s Exclusion Principle
c) Hund’s Rule of Maximum Multiplicity
d) Heisenberg’s Uncertainty Principle
View Answer
Explanation: The particles that follow Pauli’s Exclusion Principle are defined as Fermions while that don’t are called bosons. Bosons have an integral spin number.
3. The Maxwell-Boltzmann law is given by the expression ni = ________
a) \(\frac{g}{e^{\alpha+\beta E}} \)
b) \(\frac{g}{e^{\alpha+\beta E}-1} \)
c) \(\frac{g}{e^{\alpha+\beta E}+1} \)
d) \(\frac{g}{e^{\alpha+\beta E}+k} \)
View Answer
Explanation: The correct expression for the Maxwell-Boltzmann law is ni = \(\frac{g}{e^{\alpha+\beta E}+1} \), where α depends on the volume and the temperature of the gas and β is equal to 1/kT.
4. The wave function of fermions is not _________
a) Continuous
b) Single Valued
c) Symmetric
d) Differentiable
View Answer
Explanation: The particles which have antisymmetric wave function having half odd integral spin number and obey Pauli’s principle are called fermions.
5. Fermi-Dirac statistics cannot be applied to ________
a) Electrons
b) Photons
c) Fermions
d) Protons
View Answer
Explanation: Fermi-Dirac Statistics can be applied to particles having half odd integral spin number and obey Pauli’s principle which are electrons, fermions and protons. Photon has an integral spin number.
6. The distribution function is given by ________
a) \(\frac{1}{Ae\frac{E}{nT}+1}\)
b) \(\frac{1}{Ae\frac{E}{nT}-1}\)
c) \(\frac{1}{e\frac{E}{nT}+A}\)
d) \(\frac{1}{e\frac{E}{nT}-A}\)
View Answer
Explanation: The distribution function is given by \(\frac{1}{Ae\frac{E}{nT}+1}\), where A = \(e^{\frac{-E_F}{nT}}\) The energy EF is called the Fermi energy and is constant for a given system.
7. At T > 0K, the probability of a state with E > EF filled is zero.
a) True
b) False
View Answer
Explanation: At T > 0 K, the probability that a state with E > EF is filled is 1⁄2. Hence, fermi energy is the energy at which the probability of occupation is 1⁄2 at any temperature above 0 K.
8. The expression for mean energy is given by ________
a) \(\frac{3}{5}NE_F\)
b) \(\frac{2}{5}NE_F\)
c) \(\frac{3}{5}E_F\)
d) \(\frac{2}{5}E_F\)
View Answer
Explanation: The expression for the mean energy of an electron at absolute zero is given by \(\frac{3}{5}NE_F\). The expression \(\frac{3}{5}E_F\) is called the zero point energy.
9. For all the quantum states with energy greater than Fermi energy to be empty in a Fermi-Dirac system, the temperature should be ______
a) 273 K
b) 373 K
c) 0 K
d) 100 K
View Answer
Explanation: We know that the Fermi-Dirac distribution is given by:
FFD(E) = \( \frac{1}{e\frac{E-E_F}{nT}+1}\)
For all the quantum states with energy greater than Fermi energy to be empty,
FFD(E) = 0, for E > EF and FFD(E) = 1, for E < EF
Therefore, for E < EF \( \frac{1}{e\frac{E-E_F}{nT}+1}=1\)
\(e\frac{E-E_F}{nT}= 0\)
As, E < EF, E- EF < 0. Therefore, to satisfy the given statement,
T = 0 K
Thus, we can define Fermi energy as the energy of the uppermost occupied level at 0 K.
10. What is the relationship between T1 and T2?
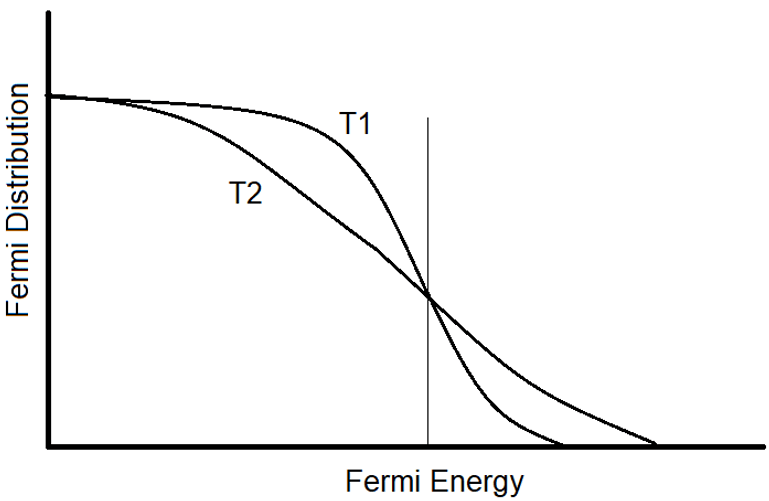
a) T1 > T2
b) T1 < T2
c) T1 = T2
d) Insufficient Information
View Answer
Explanation: The given figure shows the variation of Fermi-Dirac distribution with energy E. In this case, T2 > T1, according to the expression: FFD(E) =\( \frac{1}{e\frac{E-E_F}{nT}+1}\).
11. The density of silver is 10.5 g/cm3 and its atomic weight is 108. If each atom contributes one electron for conduction, what is the fermi energy?
a) 2.12 eV
b) 3.31 eV
c) 4.69 eV
d) 5.51 eV
View Answer
Explanation: Fermi Energy, \(E_F = \frac{h^2}{8m} (\frac{3N}{\pi v})^{2∕3}\)
Here, N /V = 10.5 X 6.02 X 1023/108
= 5.85 X 1028 m-3
Therefore, \(E_F = \frac{6.626 X 6.626}{8 X 9.1} \times 10^{-19} \times \frac{3 \times 5.585}{\pi}^{2∕3}\)
= 8.816 X 10-19J
= 5.51 eV.
12. The Fermi energy of a material is 3.45 eV. What is the zero-point energy of the material?
a) 1.02 eV
b) 2.07 eV
c) 3.45 eV
d) 4.16 eV
View Answer
Explanation: As we know, the fermi energy of the material is 3.45 eV.
Now, zero-point energy =\(\frac{3}{5}E_F\)
= 3/5 X 3.45 eV
= 2.07 eV.
13. The average energy of one electron silver is 3.306 eV. What is the fermi-energy of Silver at 0 K?
a) 2.32 eV
b) 3.78 eV
c) 4.12 eV
d) 5.51 eV
View Answer
Explanation: We know, Average Energy, E =\(\frac{3}{5}NE_F\)
Here, E = 3.306 eV, N = 1
Therefore, we get: EF = 5E/3
= 5.51 eV.
14. In Fermi-Dirac Statistics, one energy state can be occupied by more than one particle.
a) True
b) False
View Answer
Explanation: In Fermi-Dirac statistics, one energy state can be occupied by only one particle. Therefore, when one state is filled, the particle will go on to another state.
15. Which of the following is the curve for Fermi-Dirac statistics?
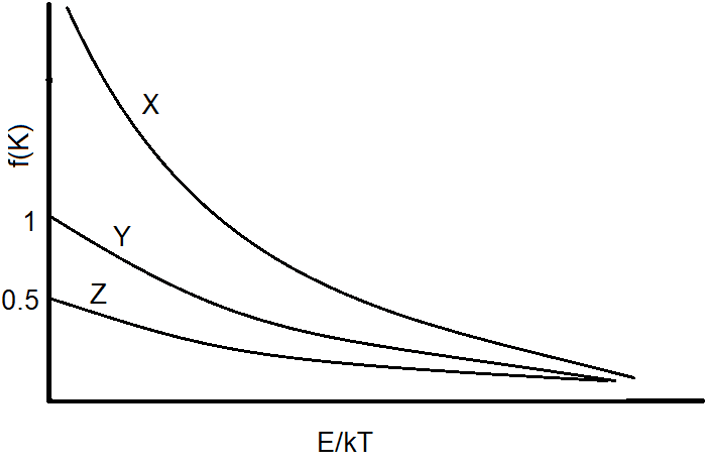
a) X
b) Y
c) Z
d) None
View Answer
Explanation: As seen the curve the order of the ration of f(K) with E/kT is in the order X > Y > Z. Here, Y is Maxwell-Boltzmann Statistics, X is Bose-Einstein Statistics and Z is Fermi-Dirac Statistics.
Sanfoundry Global Education & Learning Series – Engineering Physics.
To practice all areas of Engineering Physics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
