This set of Engineering Physics Multiple Choice Questions & Answers (MCQs) focuses on “Quantum Nature of Elastic Waves”.
1. Elastic waves in crystals are made up of _______________
a) Photons
b) Nano particles
c) Atoms
d) Phonons
View Answer
Explanation: In a crystal, when energy is provided, the lattice absorbs energy and gets excited to a higher state. When it de-excites to ground state, it releases radiation in sound-wave region, known as phonons. These waves are quantized.
2. The energy of elastic waves is given by _____________
a) nω
b) n ħω
c) nħω/2
d) (n + 1⁄2)ħω
View Answer
Explanation: The energy of a lattice vibration is quantized which is given by the expression: E = (n + ½)ħω, where w is the angular frequency of the waves.
3. Waves in the wave packets are such that they interfere constructively over a large region of space.
a) True
b) False
View Answer
Explanation: A wave packet consists of a group of waves, each of which have phases and amplitudes such that they interfere constructively over a small region of space where the particle can be located. Outside that region, they interfere destructively.
4. Which of the following is the correct expression for the group velocity?
a) υλ
b) dω/dυ
c) dE/dk
d) dE/ħdk
View Answer
Explanation: The velocity with which the wave packet moves is called the group velocity. It is equal to dω/dk, which can be further simplified to dE/ħdk, as E =ħω.
5. Which of the following is the correct relation between the group velocity and the phase velocity?
a) vg = vp + λdvp/dλ
b) vp = vg + λdvp/dλ
c) vp = vg – λdvp/dλ
d) vg = vp – λdvp/dλ
View Answer
Explanation: The relation between the phase velocity and the group velocity is given by: vg = vp – λdvp/dλ. Thus, when dvp/dλ = 0, vg = vp.
6. The motion of a wave packet is similar to _____________
a) Photons
b) Waves
c) Classical Particle
d) Quantum Particle
View Answer
Explanation: The motion of a material/classical particle is equivalent to a group of waves or a wave packet. Such an expression can be derived by using the basic principles of motion.
7. Which of the following is not a characteristic of wave function?
a) Continuous
b) Single valued
c) Differentiable
d) Physically Significant
View Answer
Explanation: The wave function has no physical significance. It merely helps in determining the state of a particle. It is the square of the wave function that has a physical significance.
8. There is an inextensible string of linear density µ. If it is given that ω = \(k\sqrt{\frac{T}{μ}}\), then what is the group velocity of the string?
a) \(\sqrt{\frac{T}{μ}}\)
b) ħ\(\sqrt{\frac{T}{μ}}\)
c) \(\frac{\hbar}{2}\sqrt{\frac{T}{μ}}\)
d) \(\frac{1}{\hbar}\sqrt{\frac{T}{μ}}\)
View Answer
Explanation: As we know, vg = dω/dk
Therefore, vg = d( k\(\sqrt{\frac{T}{μ}}\))/dk
= \(\sqrt{\frac{T}{μ}}\).
9. Ψ must be normalizable.
a) True
b) False
View Answer
Explanation: Ψ must fo to 0 as x-> infinity, y-> infinity and z -> infinity in order that ∫|Ψ|2 dv all over space be a finite constant. Thus, Ψ must be normalizable.
10. Calculate the minimum uncertainty in the momentum of a 4He atom confined to 0.40 nm.
a) 2.02 X 10-25 kg m/s
b) 2.53 X 10-25 kg m/s
c) 2.64 X 10-25 kg m/s
d) 2.89 X 10-25 kg m/s
View Answer
Explanation: We know that 4He atom is somewhere in the 0.40 nm region, therefore, Δx = 0.40 nm.
Using, Δpx ≥ \(\frac{\hbar}{\Delta x}\)
For minimum uncertainty, Δpx = 6.626 X 10-34 Js/2π X 0.40 X 10-9
= 2.64 X 10-25 kg m/s.
11. The following is a possible wave function.
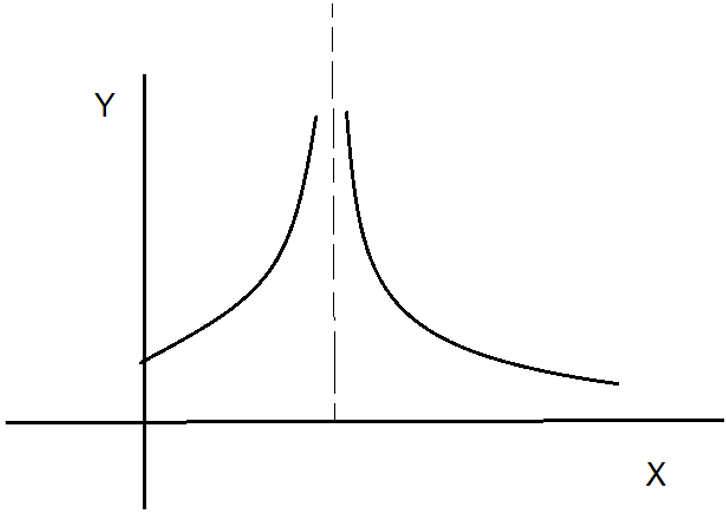
a) True
b) False
View Answer
Explanation: The following cannot be the graph of a wave function as the graph is discontinuous. A wave function should be continuous and single valued.
12. The uncertainty in the location of a particle moving with velocity 7.28 X 107m /s is two times its de-Broglie wavelength. What is the uncertainty in measuring the velocity?
a) 5.79 X 106 m/s
b) 6.12 X 106 m/s
c) 7.63 X 106 m/s
d) 8.45 X 106 m/s
View Answer
Explanation: De-Broglie wavelength, λ = h/mv
Given: Δx = 2λ = 2h/mv
Now, Δx.m.Δv = ħ
Δv = v/4π
= 5.79 X 106 m/s.
13. Energy of a wave divided by its momentum gives _____________
a) Group velocity
b) Classical Velocity
c) Phase Velocity
d) Wave velocity
View Answer
Explanation: We know, E = ħω and P = ħk. Therefore, E/P gives us w/k which is the phase velocity of the wave. Hence, Energy of a wave divided by its momentum gives us phase velocity.
14. Which of the following can be a wave function?
a) tan x
b) sin x
c) cot x
d) sec x
View Answer
Explanation: Out of all the given options, sin x is the only function, that is continuous and single-valued. All the rest of the functions are either discontinuous or double-valued.
15. At what condition, vp = vg?
a) dvp/dk = 0
b) dvp/dω = 0
c) dvp/dλ = 0
d) dvp/dμ= 0
View Answer
Explanation: As we know, the relation between the phase and group velocity is vg = vp – λdvp/dλ. Thus, as dvp/dλ = 0, vp = vg.
Sanfoundry Global Education & Learning Series – Engineering Physics.
To practice all areas of Engineering Physics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
