This set of Engineering Physics Multiple Choice Questions & Answers (MCQs) focuses on “Mass Energy Relation”.
1. The basic theorem/principle used to obtain mass-energy relation is _____________
a) Heisenberg’s Uncertainty Principle
b) Work-Energy Theorem
c) Momentum Conservation Theorem
d) Maxwell Theorem
View Answer
Explanation: To derive Einstein’s mass-energy relation, the basic principle used is Work-Energy Theorem. It states that the kinetic energy of a moving body is equal to the work done by the external force on the body from rest.
2. Which of the following is Einstein’s mass energy relation?
a) Ek = (m – m0)c2
b) E = mc2
c) E2 – p2c2 = m02c4
d) Ek = mv2/c2
View Answer
Explanation: E = mc2 is the famous Einstein mass-energy relation. It states a universal equivalence between mass and energy.
3. For Pair Production phenomenon to occur to photon must have energy, greater than or equal to ____________
a) 0.51 MeV
b) 1.02 MeV
c) 0.32 MeV
d) 0.85 MeV
View Answer
Explanation: In Pair Production, a proton with energy, greater than or equal to 1.02 MeV is required to create a pair of electron and positron. 1.02 MeV is the minimum required energy for their creation.
4. Which of the following is the momentum-energy relation?
a) E2 – p2c2 = m02c2
b) E2 – p2c2 = m02c4
c) E2 – p2c2 = m02c3
d) E2 – p2c2 = m0c2
View Answer
Explanation: Einstein’s famous momentum-energy relation shows that a particle may have energy and momentum even if its rest mass is zero, i.e., if m0 = 0.
5. In Relativistic case, as the velocity of the particle approaches the speed of light, the Kinetic energy approaches ___________
a) Zero
b) Kinetic Energy as in Non-Relativistic case
c) Rest Energy
d) Infinite
View Answer
Explanation: In Relativistic case, the expression for Kinetic Energy is: Ek = \((\frac{m_0}{\sqrt{1-\frac{v^2}{c^2}}} – m_0)c^2\)
Thus, as v -> c, v/c -> 1.
Thus, the Kinetic Energy approaches infinity, which would require an infinite amount of external work.
6. If a star radiates energy at the rate of 5 x 1020 Js-1, what is the rate at which its mass is decreasing?
a) 5.54 x 109 kgs-1
b) 4.44 x 109 kgs-1
c) 3.44 x 109 kgs-1
d) 2.44 x 109 kgs-1
View Answer
Explanation: As we know from Einstein’s mass energy relation, E = mc2.
Therefore, ΔE = Δmc2
ΔE = 5 x 1020 Js-1, c = 3 x 108 ms-1.
Δm = 5 x 1020 Js-1/ 9 x 1016m2s-2
Δm = 5.54 x 103 kgs-1.
7. What will be the rest energy of an electron?
a) 0.41 MeV
b) 0.51 MeV
c) 0.61 MeV
d) 0.71 MeV
View Answer
Explanation: We Know, rest energy = mc2
Here, m = 3.1 X 10-31 kg, c = 3 X 108 m/s
Therefore, E = 9.109 X 10-31 kg X 9 X 1016 m2/s2
= 8.198 X 10-14 J
= 0.51 MeV.
8. The binding energy of an electron to a proton (i.e., hydrogen atom) is 13.6 eV. The loss of mass in the formation of one atom of hydrogen is _____________
a) 2.42 X 10-35 Kg
b) 3.34 X 10-35 Kg
c) 4.58 X 10-35 Kg
d) 5.19 X 10-35 Kg
View Answer
Explanation: E = 13.6 eV = 13.6 X 1.6 X 10-19 J
Using Einstein’s Mass-energy relation, the loss of mass Δm = E/c2
Δm = 13.6 X 1.6 X 10-19/9 X 1016
= 2.42 X 10-35 Kg.
9. The momentum of a photon having energy 10-17J is ____________
a) 1.11 X 10-26 Kg m/s
b) 2.22 X 10-26 Kg m/s
c) 3.33 X 10-26 Kg m/s
d) 4.44 X 10-26 Kg m/s
View Answer
Explanation: We know that the rest mass of a photon is zero.
Therefore, from the momentum-energy relation
P = E/c = 10-17/3 X 108
= 3.33 X 10-26 Kg m/s.
10. Which phenomenon is shown in the figure?
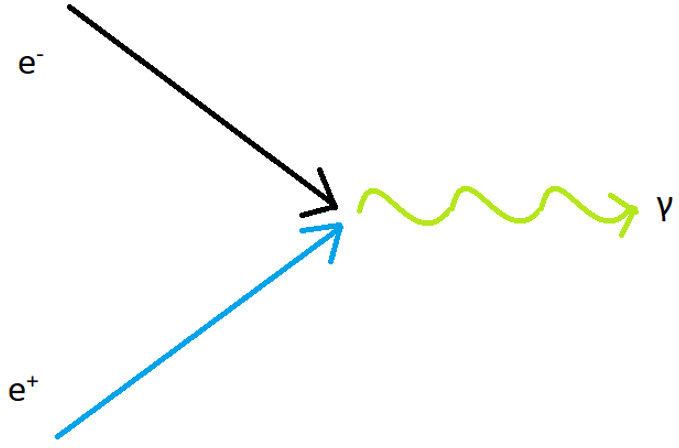
a) Pair Production
b) Photoelectric Effect
c) Compton effect
d) Pair annihilation
View Answer
Explanation: In the figure, an electron and a positron annihilate each other and release the equivalent amount of energy. This process is called Pair annihilation.
Sanfoundry Global Education & Learning Series – Engineering Physics.
To practice all areas of Engineering Physics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
