This set of Engineering Physics Multiple Choice Questions & Answers (MCQs) focuses on “Schrodinger Equation (Time Dependent Form)”.
1. Which of the following is the correct expression for the Schrödinger wave function?
a) \(i\hbar \frac{d\Psi}{dt} = -i\frac{\hbar}{2m} \frac{\partial\Psi}{\partial x}+ U\Psi\)
b) \(i\hbar \frac{d\Psi}{dt} = -i\frac{\hbar}{2m} \frac{\partial^2 \Psi}{\partial x^2}+ U\Psi\)
c) \(i\hbar \frac{d\Psi}{dt} = -i\frac{\hbar^z}{2m} \frac{\partial\Psi}{\partial x}+ U\Psi\)
d) \(i\hbar \frac{d\Psi}{dt} = -i\frac{\hbar^z}{2m} \frac{\partial^2\Psi}{\partial x^2}+ U\Psi \)
View Answer
Explanation: The correct expression for the Schrödinger wave equation is \(i\hbar \frac{d\Psi}{dt}= -i\frac{\hbar^z}{2m} \frac{\partial^2\Psi}{\partial x^2}+ U\Psi \). Schrodinger equation is a basic principle in itself.
2. For a quantum wave particle, E = _____________
a) ℏ k
b) ℏ ω
c) ℏ ω/2
d) ℏ k/2
View Answer
Explanation: The Energy of a wave particle is given as ℏ ω while the momentum of the particle is given as ℏ k. These are the desired relation.
3. Schrodinger Wave equation can be derived from Principles of Quantum Mechanics.
a) True
b) False
View Answer
Explanation: Schrodinger equation is a basic principle in itself. It cannot be derived from other principles of physics. Only, it can be verified with other principles.
4. Which of the following can be a wave function?
a) tan x
b) sin x
c) cot x
d) sec x
View Answer
Explanation: Out of all the given options, sin x is the only function, that is continuous and single-valued. All the rest of the functions are either discontinuous or double-valued.
5. Which of the following is not a characteristic of wave function?
a) Continuous
b) Single valued
c) Differentiable
d) Physically Significant
View Answer
Explanation: The wave function has no physical significance. It merely helps in determining the state of a particle. It is the square of the wave function that has a physical significance.
6. Find the function, f(x), for which X f(x) = \(-\frac{i}{\hbar}a^2p_xf(x),\) where a is the real quantity.
a) ke-x2
b) ke-x2/2a
c) ke-x2/2a2
d) ke-x2/2a
View Answer
Explanation: Now, given that, X f(x) = \(-\frac{i}{\hbar}a^2p_xf(x).\)
X f(x) = \(-\frac{i}{\hbar}a^2p_xf(x)/dx\)
df/f = -xdx/a2
ln f = -x2/2a2 + C
f = ke-x2/2a2.
7. dΨ/dx must be zero.
a) True
b) False
View Answer
Explanation: For a wave function, dΨ/dx, must be continuous and single-valued everywhere, just like Ψ. Also, Ψ must be normalizable.
8. Any wave function can be written as a linear combination of _________________
a) Eigen Vectors
b) Eigen Values
c) Eigen Functions
d) Operators
View Answer
Explanation: A wave function describes the state of a particle. It does not have a physical significance. Moreover, it can be written as a linear combination of Eigen functions, i.e., Ψ(x) = AF(x) + BG(x).
9. The Schrödinger is a differential equation.
a) True
b) False
View Answer
Explanation: The Schrodinger wave equation generated is a partial differential equation. It is a basic principle in itself and cannot be derived from other principles of physics. There are two types of partial differential equation time dependent form and steady-state form.
10. Which of the following can be a solution of Schrodinger equation?
a) 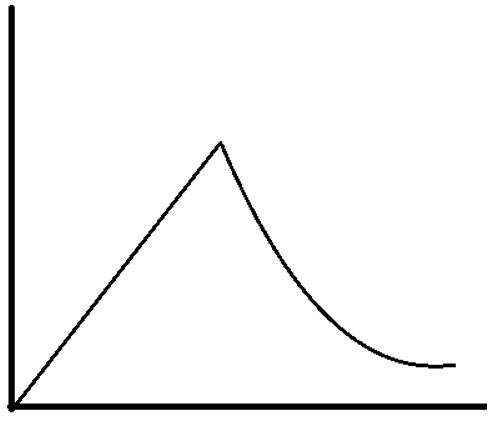
b) 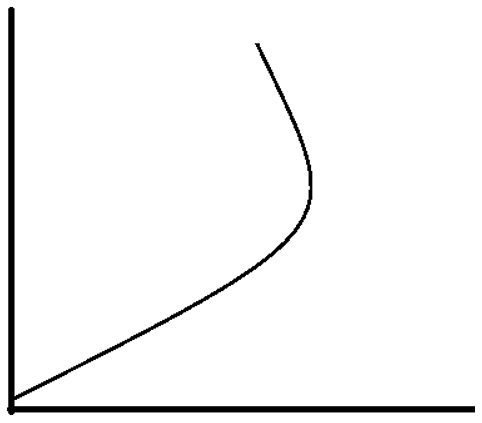
c) 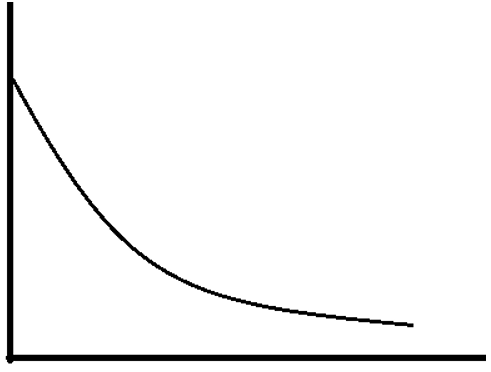
d) 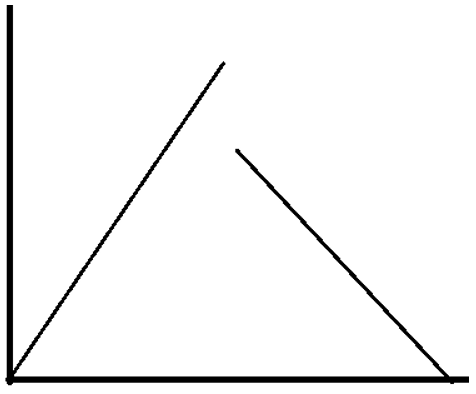
View Answer
Explanation: Out of the following, only the below diagram can be the solution of the Schrodinger Wave equation. because other diagram does not have a continuous dΨ/dx. Some diagrams are double valued and discontinuous also.

Sanfoundry Global Education & Learning Series – Engineering Physics.
To practice all areas of Engineering Physics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
