This set of Engineering Physics Multiple Choice Questions & Answers (MCQs) focuses on “Finite Potential Well”.
1. In a finite Potential well, the potential energy outside the box is ____________
a) Zero
b) Infinite
c) Constant
d) Variable
View Answer
Explanation: In a finite potential well, the potential energy of the particle outside the box is a finite constant unlike infinite potential well, where the potential energy outside the box was infinite.
2. The Schrodinger for the particle inside a finite potential well becomes ____________
a) x > 0
b) x < 0
c) 0 < X < L
d) x > L
View Answer
Explanation: The particle cannot exist outside the box, as it cannot have infinite amount of energy. Thus, it’s wave function is between 0 and L, where L is the length of the side of the box.
3. When the particle strikes the wall of the well, it bounces off completely.
a) True
b) False
View Answer
Explanation: Whenever the particle is incident on the wall of the potential well, there is a probability that the particle may move on to the next region even though it’s energy is less than the potential energy of the barrier.
4. The Energy of the particle is proportional to ____________
a) n
b) n-1
c) n2
d) n-2
View Answer
Explanation: In a particle inside a box, the energy of the particle is directly proportional to the square of the quantum state in which the particle currently is n2.
5. For a particle inside a box of finite potential well, the particle is most stable at what position of x?
a) x > L
b) x < 0
c) 0 < x < L
d) Not stable in any state
View Answer
Explanation: The particle is most stable when it is inside the box of finite potential well. In that case, the potential energy of the particle is zero.
6. When the Schrodinger equation is solved for E > Vo, the solutions will be __________
a) Non-oscillatory
b) Oscillatory Inside
c) Oscillatory Outside
d) Oscillatory inside as well as outside
View Answer
Explanation: If we solve the time-independent Schrödinger equation for an energy E > Vo, the solutions will be oscillatory both inside and outside the well. Thus, the solution is never square integrable; that is, it is always a non-normalizable state.
7. Particle in a box of finite potential can never be at rest.
a) True
b) False
View Answer
Explanation: If the particle in a box has zero energy, it will be at rest inside the well and it violates the Heisenberg’s Uncertainty Principle. Thus, the minimum energy possessed by a particle is not equal to zero.
8. What is the minimum Energy possessed by the particle in a box?
a) Zero
b) \(\frac{\pi^2\hbar^2}{2mL^2}\)
c) \(\frac{\hbar^2}{2m}\)
d) \(\frac{\pi^2\hbar}{2m}\)
View Answer
Explanation: The minimum energy possessed by a particle inside a box in a finite potential well is equal to \(\frac{\hbar^2}{2m}\). The particle can never be at rest, as it will violate Heisenberg’s Uncertainty Principle.
9. The wave function of a particle in a box is given by ____________
a) A sin(kx)
b) A cos(kx)
c) Asin(kx) + Bcos(kx)
d) A sin(kx) – B cos(kx)
View Answer
Explanation: The wave function for the particle in a box is given by: Asin(kx)+Bcos(kx). The Energy possessed by the particle is given by: \(\frac{n^2\hbar}{2m}\).
10. What does the following figure shows?
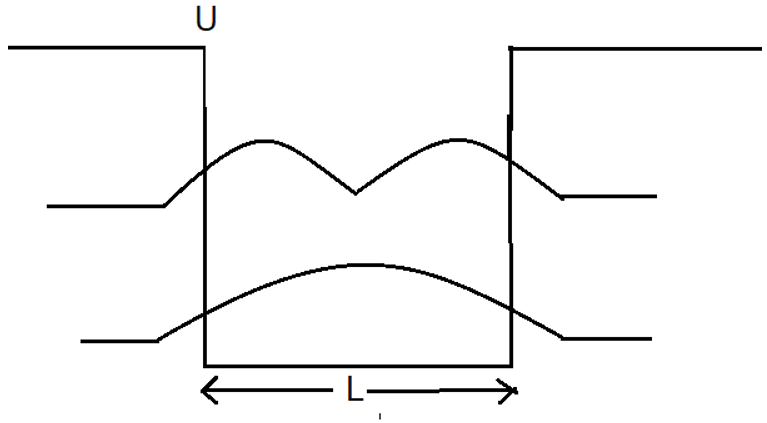
a) Wave function for Infinite Potential Well
b) Wave function for Finite Potential Well
c) Probability Density function for Infinite Potential Well
d) Probability Density function for Finite Potential Well
View Answer
Explanation: The given figure shows the probability densities of a particle in a finite potential well. The particle has a certain probability of being outside the well.
Sanfoundry Global Education & Learning Series – Engineering Physics.
To practice all areas of Engineering Physics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
