This set of Engineering Physics Multiple Choice Questions & Answers (MCQs) focuses on “Bose-Einstein Distribution”.
1. Bosons have symmetrical wave functions. They do not obey ______
a) Aufbau principle
b) Pauli’s Exclusion Principle
c) Hund’s Rule of Maximum Multiplicity
d) Heisenberg’s Uncertainty Principle
View Answer
Explanation: The particles that follow Pauli’s Exclusion Principle are defined as Fermions while that don’t are called bosons. Bosons have an integral spin number.
2. Bose-Einstein statistics is for the ________
a) Distinguishable particles
b) Symmetrical Particles
c) Particles with half integral spin
d) Particles with integral spin
View Answer
Explanation: The Bose-Einstein statistics is for the indistinguishable particles with integral spin. They do not obey Pauli’s exclusion principle.
3. The Bose-Einstein Statistics is given by the expression ni = _______
a) \(\frac{g}{e^{\alpha+\beta E}}\)
b) \(\frac{g}{e^{\alpha+\beta E}-1}\)
c) \(\frac{g}{e^{\alpha+\beta E}+1}\)
d) \(\frac{g}{e^{\alpha+\beta E}+k}\)
View Answer
Explanation: The correct expression for the Bose-Einstein law is ni = \(\frac{g}{e^{\alpha+\beta E}-1}\), where α depends on the volume and the temperature of the gas and β is equal to 1/kT.
4. The difference between fermions and bosons is that bosons’ wave function is _______
a) Continuous
b) Single Valued
c) Symmetric
d) Differentiable
View Answer
Explanation: Bosons are the particles which have symmetric wave function. Fermions are the particles with asymmetric wave function.
5. Bose-Einstein statistics can be applied to _______
a) Electrons
b) Photons
c) Fermions
d) Protons
View Answer
Explanation: Bose-Einstein Statistics can be applied to particles having integral spin number and do not obey Pauli’s principle. Photon comes under this category.
6. In Bose-Einstein Statistics, one energy state can be occupied by more than one particle.
a) True
b) False
View Answer
Explanation: In Bose-Einstein statistics, one energy state can be occupied by only one particle, as we already know that the Pauli’s exclusion principle is not obeyed in their case. The particles have integral spin and have a symmetric wave function.
7. When bosons are cooled to a low enough temperature, their behavior changes.
a) True
b) False
View Answer
Explanation: The given statement is true. This process of cooling down bosons is called Bose-Einstein condensation and the product formed is called Bose-Einstein condensate.
8. Helium shows Bose-Einstein condensation below what temperature?
a) 100.5 K
b) 12.3 K
c) 5.12 K
d) 2.13 K
View Answer
Explanation: When cooled below 2.13 K, a transition occurs and liquid helium in this state shows super fluidity. It shows to have no viscosity and it can go through very narrow slits. It becomes a Bose-Einstein Condensate.
9. During Bose-Einstein condensation all the atoms fall back to the _______
a) Ground state
b) First exited state
c) Highest Exited state
d) Insufficient information
View Answer
Explanation: During Bose-Einstein Condensation, the temperature of the material is so low, that all the atoms fall to the ground state. This low-temperature collection of ground-state bosons is called Bose-Einstein Condensate.
10. Which of the following is the curve for Bose-Einstein statistics?
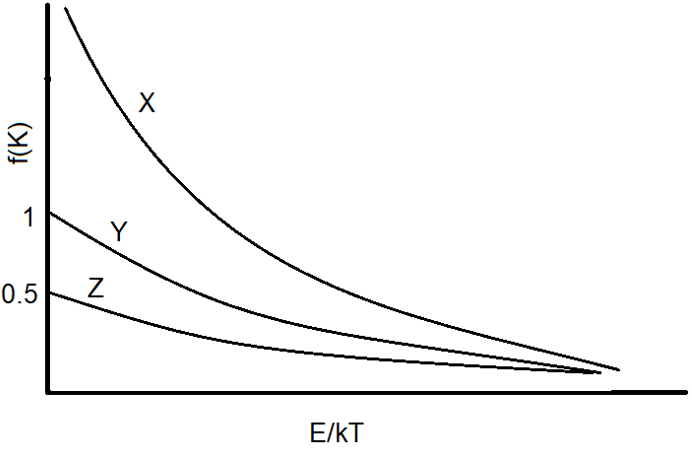
a) X
b) Y
c) Z
d) None
View Answer
Explanation: As seen the curve the order of the ration of f(K) with E/kT is in the order X > Y > Z. Here, Y is Maxwell-Boltzmann Statistics, X is Bose-Einstein Statistics and Z is Fermi-Dirac Statistics.
Sanfoundry Global Education & Learning Series – Engineering Physics.
To practice all areas of Engineering Physics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
