This set of Engineering Physics Multiple Choice Questions & Answers (MCQs) focuses on “Particle in a Box”.
1. The walls of a particle in a box are supposed to be ____________
a) Small but infinitely hard
b) Infinitely large but soft
c) Soft and Small
d) Infinitely hard and infinitely large
View Answer
Explanation: The simplest quantum-mechanical problem is that of a particle in a box with infinitely hard walls and are infinitely large.
2. The wave function of the particle lies in which region?
a) x > 0
b) x < 0
c) 0 < X < L
d) x > L
View Answer
Explanation: The particle cannot exist outside the box, as it cannot have infinite amount of energy. Thus, it’s wave function is between 0 and L, where L is the length of the side of the box.
3. The particle loses energy when it collides with the wall.
a) True
b) False
View Answer
Explanation: The total energy of the particle inside the box remains constant. It does not loses energy when it collides with the wall.
4. The Energy of the particle is proportional to __________
a) n
b) n-1
c) n2
d) n-2
View Answer
Explanation: In a particle inside a box, the energy of the particle is directly proportional to the square of the quantum state in which the particle currently is.
5. For a particle inside a box, the potential is maximum at x = ___________
a) L
b) 2L
c) L/2
d) 3L
View Answer
Explanation: In a box with infinitely high barriers with infinitely hard walls, the potential is infinite when x = 0 and when x = L.
6. The Eigen value of a particle in a box is ___________
a) L/2
b) 2/L
c) \(\sqrt{L/2}\)
d) \(\sqrt{2/L}\)
View Answer
Explanation: The wave function for the particle in a box is normalizable, when the value of the coefficient of sin is equal to \(\sqrt{2/L}\)
. It is the Eigen value of the wave function.
7. Particle in a box can never be at rest.
a) True
b) False
View Answer
Explanation: If the particle in a box has zero energy, it will be at rest inside the well and it violates the Heisenberg’s Uncertainty Principle. Thus, the minimum energy possessed by a particle is not equal to zero.
8. What is the minimum Energy possessed by the particle in a box?
a) Zero
b) \(\frac{\pi^2\hbar^2}{2mL^2}\)
c) \(\frac{\pi^2\hbar^2}{2mL}\)
d) \(\frac{\pi^2\hbar}{2mL}\)
View Answer
Explanation: The minimum energy possessed by a particle inside a box with infinitely hard walls is equal to \(\frac{\pi^2\hbar^2}{2mL^2}\). The particle can never be at rest, as it will violate Heisenberg’s Uncertainty Principle.
9. The wave function of a particle in a box is given by ____________
a) \(\sqrt{\frac{2}{L}}sin\frac{nx}{L}\)
b) \(\sqrt{\frac{2}{L}}sin\frac{n\pi x}{L}\)
c) \(\sqrt{\frac{2}{L}}sin\frac{x}{L}\)
d) \(\sqrt{\frac{2}{L}}sin\frac{\pi x}{L}\)
View Answer
Explanation: The wave function for the particle in a box is given by: \(\sqrt{\frac{2}{L}}sin\frac{n\pi x}{L}\). The Energy possessed by the particle is given by: \(\frac{n^2\pi^2\hbar^2}{2mL^2}\).
10. The wave function for which quantum state is shown in the figure?
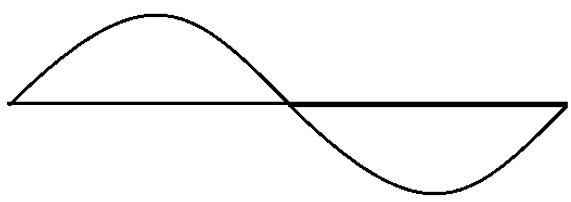
a) 1
b) 2
c) 3
d) 4
View Answer
Explanation: The shown wave function is for the 2nd principal quantum number, i.e., it is the wave function for the state when n = 2.
11. Calculate the Zero-point energy for a particle in an infinite potential well for an electron confined to a 1 nm atom.
a) 3.9 X 10-29 J
b) 4.9 X 10-29 J
c) 5.9 X 10-29 J
d) 6.9 X 10-29 J
View Answer
Explanation: Here, m = 9.1 X 10-31 kg, L = 10-9m.
Therefore, E = \(\frac{\pi^2\hbar^2}{2mL^2}\)
= 3.14 X 3.14 X 1.05 X 1.05 X 10-68/ 2 X 9.1 X 10-31 X 10-9
= 5.9 X 10-29 J.
Sanfoundry Global Education & Learning Series – Engineering Physics.
To practice all areas of Engineering Physics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
