This set of Engineering Physics Multiple Choice Questions & Answers (MCQs) focuses on “Schrodinger Equation (Steady State Form)”.
1. Which of the following is the correct expression for the steady-state form of Schrödinger wave function?
a) \(P\Psi= -i\frac{\hbar}{2m}\frac{\partial\Psi}{\partial x}+U\Psi\)
b) \(E\Psi= -i\frac{\hbar}{2m}\frac{\partial^2\Psi}{\partial x^2}+U\Psi\)
c) \(E\Psi = -i\frac{\hbar^z}{2m}\frac{\partial\Psi/\partial x}+U\Psi\)
d) \(E\Psi = -i\frac{\hbar^z}{2m}\frac{\partial^2\Psi}{\partial x^2}+U\Psi\)
View Answer
Explanation: The correct expression for the Steady state form of the Schrödinger wave equation is \(E\Psi = -i\frac{\hbar^z}{2m}\frac{\partial^2\Psi}{\partial x^2}+U\Psi\). It is different from the time-dependent for, as it depends on position of the particle only.
2. Which function is considered independent of time to achieve the steady state form?
a) Ψ
b) dΨ/dt
c) d2Ψ/dx2
d) U
View Answer
Explanation: The potential energy of a particle is considered to not depend on time explicitly, the forces that act on it, and hence U, vary with the position only.
3. For 3-D system, the Schrödinger equation changes.
a) True
b) False
View Answer
Explanation: Schrodinger equation is a basic principle. When considered for a 3-D system, only the new dimensions, in which the equation was considered, are added.
4. The Steady-state form of Schrodinger wave equation is _____________
a) Linear
b) Quadratic
c) Differential equation
d) Derivable
View Answer
Explanation: The Steady-state Schrodinger Wave equation is a linear in the wave function Ψ. It means, that no term has \Psi with a degree greater than 1.
5. The values of Energy for which Schrodinger’s steady state equation can be solved is called as _____________
a) Eigen Vectors
b) Eigen Values
c) Eigen Functions
d) Operators
View Answer
Explanation: Eigen values are the value of Energy for which Schrodinger’s steady state equation can be solved. The corresponding wave function is called Eigen Function.
6. The Energy levels are proportional to ______________
a) n
b) n-1
c) n2
d) n-2
View Answer
Explanation: The energy levels for which the Schrodinger’s steady state equation can be solved is inversely proportional to the square of quantum number.
7. Total Energy is quantized but not angular momentum of the quantum particle.
a) True
b) False
View Answer
Explanation: Both the Total energy and the angular momentum of the quantum particle is quantized. In case of Hydrogen atoms, L = \(\sqrt{l(l+1)\hbar}\), where l = 0, 1, 2, …. (n-1).
8. Which quantity is said to be degenerate when HΨn = EnΨn?
a) Eigen Vectors
b) Eigen Values
c) Eigen Functions
d) Operators
View Answer
Explanation: In such a case, when there is corresponding to each Eigen value there is only one Eigen function, the Eigen function is known as degenerate.
9. For a box with infinitely hard walls, the potential is maximum at _____________
a) L
b) 2L
c) L/2
d) 3L
View Answer
Explanation: In a box with infinitely high barriers with infinitely hard walls, the potential is infinite when x = 0 and when x = L.
10. Which device is shown in the following figure?
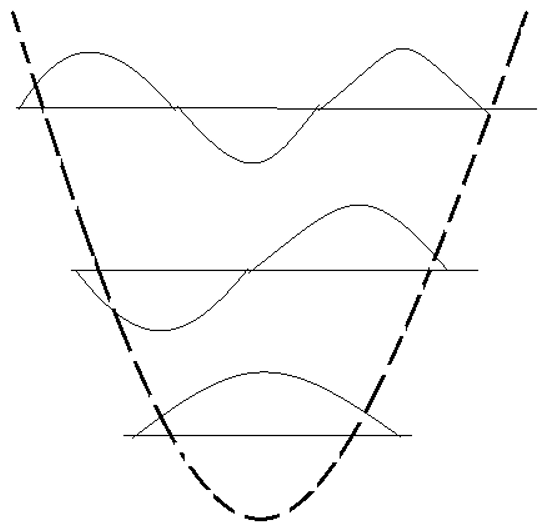
a) Particle in a Box
b) Harmonic Oscillator
c) SHM
d) Atomic spectroscope
View Answer
Explanation: The following figure shows a Harmonic oscillator. The energy levels in this device are quantize and the lowest energy is not equal to zero.
Sanfoundry Global Education & Learning Series – Engineering Physics.
To practice all areas of Engineering Physics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
