This set of Engineering Physics Multiple Choice Questions & Answers (MCQs) focuses on “Maxwell Boltzmann Statistics”.
1. Phase space is a ________
a) 3 Dimensional Space
b) 4 Dimensional Space
c) 5 Dimensional Space
d) 6 Dimensional Space
View Answer
Explanation: Phase space is a 6 Dimensional space, consisting of the position in x, y, and z directions and its momentum in these directions.
2. Maxwell-Boltzmann law is for the ________
a) Distinguishable particles
b) Indistinguishable Particles
c) Particles with half integral spin
d) Particles with integral spin
View Answer
Explanation: The Maxwell-Boltzmann statistics is for the distinguishable particles, which are basically the classical particles like atoms and molecules.
3. The Maxwell-Boltzmann law is given by the expression ________
a) \(\frac{1}{e^{(\frac{E}{kT})}} \)
b) \(\frac{1}{e^{(1+\frac{E}{kT})}} \)
c) \(\frac{1}{e^{(α+\frac{E}{kT})}} \)
d) \(\frac{1}{e^{(α+\frac{nE}{kT})}}\)
View Answer
Explanation: The correct expression for the Maxwell-Boltzmann law is \(\frac{1}{e^{(α+\frac{E}{kT})}} \), where k is the Boltzmann constant with value 1.98 X 10-23 J/K and T is the Temperature. The constant α depends on the volume and the temperature of the gas.
4. Maxwell-Boltzmann statistics cannot be applied to _____________
a) Atoms
b) Molecules
c) Photons
d) Lattice
View Answer
Explanation: Maxwell-Boltzmann can only be applied to particles which are distinguishable. Photons are indistinguishable from one other.
5. The ratio of rms velocity to most probable velocity is ________
a) √3 : √2
b) √2 : √3
c) 3 : 2
d) 2 : 3
View Answer
Explanation: As we know, vrms = \(\sqrt{\frac{3RT}{M}}\, and\, v_p = \sqrt{\frac{2RT}{M}}\). They are derived from Maxwell’s speed distribution law. By dividing them, we get: vrms:vp = √3 : √2
6. The average kinetic energy associated with each degree of freedom is ________
a) kT
b) 2kT
c) kT/2
d) kT/4
View Answer
Explanation: According to the law of equipartition of energy, the average kinetic energy associated with each degree of freedom is kT/2. The total number of independent quantities are called its degree of freedom.
7. The density of molecules is maximum at which speed?
a) Vrms
b) Vp
c) Vmean
d) Vinst
View Answer
Explanation: Most of the particles are moving with the most probable speed. As the velocity increases further, the density of molecules moving with that particular speed decreases.
8. What would be the most probable velocity for one Oxygen molecule at 300 K?
a) 612 m/s
b) 714 m/s
c) 798 m/s
d) 821 m/s
View Answer
Explanation: Mass of one Oxygen molecule = 32 g/mol
= 32 X 10-3/6.022 X 1023
= 5.31 X 10-26 Kg
Now,\(V_p = \sqrt{\frac{2kT}{M}}\)
Here, T = 300 K, k = 1.98 X 1023 and M = 32
Therefore, \(V_p = \sqrt{\frac{2X 1.98X 30}{5.31}} \) X 104
= 714 m/s.
9. Mass of A is 4 times that of B. What is the ratio of their mean velocities?
a) 1 : 4
b) 4 : 1
c) 1 : 2
d) 2 : 1
View Answer
Explanation: As we know, mean velocity = \(\sqrt{\frac{8kT}{\pi M}}\)
Now, Ma = 4Mb
Therefore, Va = \(\sqrt{\frac{8kT}{\pi M}}\)
And Vb = \(\sqrt{\frac{8kT}{4\pi M}}\)
Dividing we get: Va : Vb = 1:√4
= 1 : 2.
10. From the figure, what is the highest temperature?
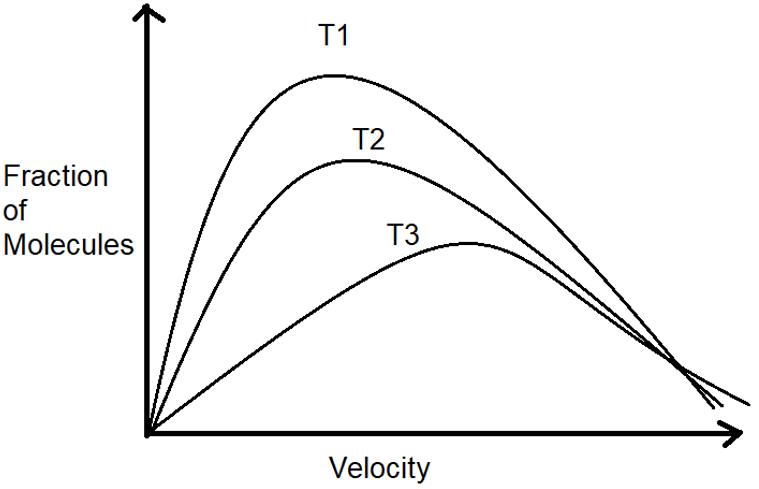
a) T1
b) T2
c) T3
d) Insufficient Information
View Answer
Explanation: As we know, as the temperature increases, the maximum velocity of the particle decreases and the density of the particles moving with higher speed increases. Thus, the correct option is T3.
11. The total Kinetic Energy of the gas particles is dependent on Temperature only.
a) True
b) False
View Answer
Explanation: As we know, the total kinetic energy of the gas particles = 3nRT/2. Hence, it depends on temperature as well as the number of moles of the gas particle.
12. As the temperature is increased, molecules moving with lower speed increases.
a) True
b) False
View Answer
Explanation: As the temperature is increased, the number of molecules travelling with lower speeds decreases whereas those travelling with higher speeds increases.
13. What is the Kinetic Energy of 2 g of oxygen at -23℃?
a) 186.2 J
b) 194.86 J
c) 201.45 J
d) 256.32 J
View Answer
Explanation: As we know, KE = 3nRT/2
Here, T = 250 K and R = 8.314 J/K
n = 2/32 = 1/16 mol
Therefore, KE = 3 X 8.314 X 250/32
= 194.86 J.
14. What is the rms speed of methane at 27℃?
a) 450 m/s
b) 532 m/s
c) 678 m/s
d) 745 m/s
View Answer
Explanation: As we know, \(v_{rms} = \sqrt{\frac{3kT}{M}}\)
Here, T = 300 K, k = 1.38 X 10-23 J/K, M = 16/6.022 X 10-26 = 2.65 X 10-26
Therefore, \(v_{rms} = \sqrt{\frac{3X 30 X 1.38}{2.65}}\) X 102
= 678 m/s.
15. Which one of the following is the most probable speed?
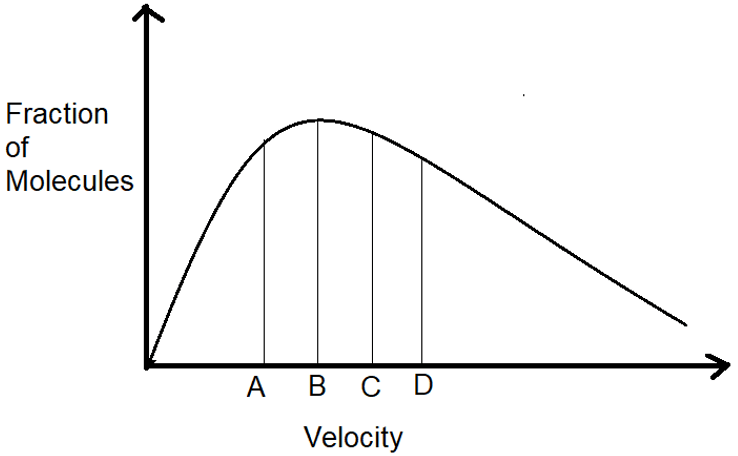
a) A
b) B
c) C
d) D
View Answer
Explanation: As we know, the most probable speed is the speed at which most of the particles are moving. Thus, as we can see, most of the particles are moving when the velocity is B. Thus, it is the most probable velocity.
Sanfoundry Global Education & Learning Series – Engineering Physics.
To practice all areas of Engineering Physics, here is complete set of 1000+ Multiple Choice Questions and Answers.
