This set of Class 10 Maths Chapter 7 Multiple Choice Questions & Answers (MCQs) focuses on “Coordinate Geometry – Area of Triangle”.
1. What will be the area of a triangle whose vertices are (3, 1), (0, 4) and (5, 9)?
a) 5 units
b) -5 units
c) -15 units
d) 15 units
View Answer
Explanation: We know that, area of triangle = \(\frac {1}{2}\){x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2 )}
The coordinates of vertices of the triangle are (3, 1), (0, 4) and (5, 9).
The area of triangle = \(\frac {1}{2}\){3(4 – 9) + 0(9 – 1) + 5(1 – 4) } = \(\frac {1}{2}\) {-15 + 0 – 15} = \(\frac {-30}{2}\) = -15 units
Since area of triangle cannot be zero. So area of triangle is 15 units.
2. What will be the area of the quadrilateral ABCD whose vertices are A (8, 6), B (9, 0), C (1, 2) and D (3, 4)?
a) -20 units
b) 26 units
c) 23 units
d) 3 units
View Answer
Explanation: Area of quadrilateral = Area of ∆ABC + Area of ∆ADC
We know that, area of triangle = \(\frac {1}{2}\){x1 (y2 – y3) + x2(y3 – y1) + x3(y1 – y2)}
The coordinates of vertices of the triangle are (8, 6), (9, 0) and (1, 2).
The area of triangle = \(\frac {1}{2}\){8(0 – 2) + 9(2 – 6) + 1(6 – 0)} = \(\frac {1}{2}\) { – 16 – 36 + 6} = \(\frac {-46}{2}\) = – 23 units
The area of triangle cannot be zero. So, Area of ∆ABC = 23 units
We know that, area of triangle = \(\frac {1}{2}\){x1(y2 – y3) + x2(y3 – y1) + x3 (y1 – y2)}
The coordinates of vertices of the triangle are (8, 6), (3, 4) and (1, 2).
The area of triangle = \(\frac {1}{2}\) {8(4 – 2) + 3(2 – 6) + 1(6 – 4)} = \(\frac {1}{2}\) {16 – 12 + 2} = \(\frac {6}{2}\) = 3 units
So, Area of ∆ADC = 3 units
Area of quadrilateral = Area of ∆ABC + Area of ∆ADC = 23 + 3 = 26 units
3. What will be the area of triangle PQR formed by joining the midpoints of the sides of the triangle whose vertices are (3, 3), (9, 9) and (4, 6)?
a) \(\frac {1}{2}\) units
b) \(\frac {3}{2}\) units
c) \(\frac {3}{5}\) units
d) \(\frac {5}{2}\) units
View Answer
Explanation:
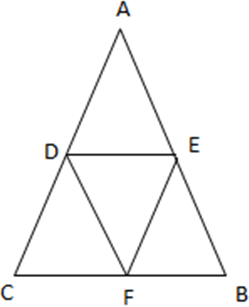
ABC is the triangle formed by the coordinates A (3, 3), B (9, 9) and C (4, 6) and DEF is the triangle formed by joining the midpoints of AC, BC, AB.
D is the midpoint of AC. Coordinates of D = \( ( \frac {x_1+x_2}{2}, \frac {y_1+y_2}{2} ) = ( \frac {3+4}{2}, \frac {3+6}{2} ) = ( \frac {7}{2}, \frac {9}{2} ) \)
E is the midpoint of AB. Coordinates of E = \( ( \frac {x_1+x_2}{2}, \frac {y_1+y_2}{2} ) = ( \frac {3+9}{2}, \frac {3+9}{2} ) = ( \frac {12}{2}, \frac {12}{2} ) \) = (6, 6)
F is the midpoint of BC. Coordinates of F = \( ( \frac {x_1+x_2}{2}, \frac {y_1+y_2}{2} ) = ( \frac {9+4}{2}, \frac {9+6}{2} ) = ( \frac {13}{2}, \frac {15}{2} ) \)
The area of triangle formed by D \( ( \frac {7}{2}, \frac {9}{2} ) \), E (6, 6) and F\( ( \frac {13}{2}, \frac {15}{2} ) \)
We know that, area of triangle = \(\frac {1}{2}\){x1 (y2 – y3 ) + x2 (y3 – y1 ) + x3 (y1 – y2 )}
The coordinates of vertices of the triangle are \( ( \frac {7}{2}, \frac {9}{2} ) \), (6, 6) and \( ( \frac {13}{2}, \frac {15}{2} ) \).
The area of triangle = \(\frac {1}{2} \{ \frac {7}{2}\) (6 – \(\frac {15}{2}\)) + 6(\(\frac {15}{2} – \frac {9}{2}\)) + \(\frac {13}{2} ( \frac {9}{2} – 6 ) \} \) = \(\frac {1}{2} \{ – \frac {21}{4}\) + 18 – \(\frac {39}{4} \} = \frac {3}{2} \) units
4. If the points A, B, C is collinear then the area of the triangle will be zero.
a) True
b) False
View Answer
Explanation: We know that, area of triangle = \(\frac {1}{2}\){x1 (y2 – y3 ) + x2 (y3 – y1 ) + x3 (y1 – y2 )}
Let us assume the vertices of the triangle are (0, 0), (0, 4) and (0, 9).
The area of triangle = \(\frac {1}{2}\) {0(4 – 9) + 0(9 – 0) + 0(0 – 4) } = \(\frac {1}{2}\){0} = 0 units
Hence, the area of triangle will be zero if the points are collinear.
5. What will be the area of triangle formed by joining the points P (2, 3), Q (4, 6) and R (6, 9)?
a) 0
b) 2
c) 3
d) 4
View Answer
Explanation: We know that, area of triangle = \(\frac {1}{2}\){x1 (y2 – y3 ) + x2 (y3 – y1 ) + x3 (y1 – y2 )}
Let us assume the vertices of the triangle are (2, 3), (4, 6) and (6, 9).
The area of triangle = \(\frac {1}{2}\) {2(6 – 9) + 4(9 – 3) + 6(3 – 6) } = \(\frac {1}{2}\){0} = 0 units
Hence, the area of triangle is zero, the points are collinear.
6. What will be the value of p, for which the points (-3, p), (-1, 2) and (1, 1) are collinear?
a) p = -4
b) p = 4
c) p = 3
d) p = -3
View Answer
Explanation: We know that, area of triangle = \(\frac {1}{2}\){x1 (y2 – y3 ) + x2 (y3 – y1 ) + x3 (y1 – y2 )}
The vertices of the triangle are (-3, p), (-1, 2) and (1, 1)
The area of triangle = \(\frac {1}{2}\) {-3(2 – 1) + (-1)(1 – p) + 1(p – 2)} = \(\frac {1}{2}\) {-3 – 1 + p + p – 2} = \(\frac {-6 + 2p}{2}\) = – 3 + p
Since, the points are collinear; the area of triangle will be zero.
-3 + p = 0
p = 3
7. The points A (3, 0), B (4, 5) and C (6, 7) are collinear.
a) True
b) False
View Answer
Explanation: We know that, area of triangle = \(\frac {1}{2}\){x1 (y2 – y3 ) + x2 (y3 – y1 ) + x3 (y1 – y2 )}
Let us assume the vertices of the triangle are A (3, 0), B (4, 5) and C (6, 7)
The area of triangle = \(\frac {1}{2}\) {3(5 – 7) + 4(7 – 0) + 6(0 – 5)} = \(\frac {1}{2}\) {-8} = – 4 units
Since, the area of triangle is not zero.
Therefore, the points are not collinear.
8. Three points A (x1, y1), B (x2, y2) and C (x3, y3) are collinear only when \(\frac {1}{2}\) {x1 (y2 – y3 ) + x2 (y3 – y1 ) + x3 (y1 – y2 ) } = 0.
a) False
b) True
View Answer
Explanation: Consider three points (-3, 3), (-1, 2) and (1, 1)
We know that, area of triangle = \(\frac {1}{2}\){x1 (y2 – y3 ) + x2 (y3 – y1 ) + x3 (y1 – y2)}
The area of triangle = \(\frac {1}{2}\) {-3(2 – 1) + (-1)(1 – 3) + 1(3 – 2)} = \(\frac {1}{2}\) {-3 – 1 + 3 + 3 – 2} = \(\frac {0}{2}\) = 0
Hence if the points are collinear the area of triangle is zero.
9. If A (x1, y1), B (x2, y2) and C (x3, y3) are the vertices of a triangle ABC, then its area is given by \(\frac {1}{2}\) {x1 (y2 – y3 ) + x2 (y3 – y1 ) + x3 (y1 – y2 ) }
a) True
b) False
View Answer
Explanation:
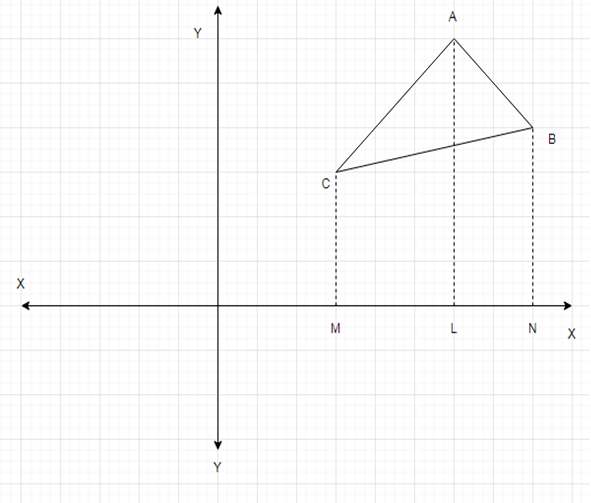
A (x1, y1), B (x2, y2) and C (x3, y3) are the vertices of a triangle ABC.
Draw AL, CM, BN perpendicular to x – axis.
Then, ML = (x1 – x2), LN = (x3 – x1) and MN = (x3 – x2).
∴ area of ∆ABC = ar(trap.BMLA) + ar(trap.ALNC) + ar(trap.BMNC)
= {\(\frac {1}{2}\) (AL + BM) × ML} + {\(\frac {1}{2}\) (AL + CN) × LN} – {\(\frac {1}{2}\) (CN + BM) × MN}
= {\(\frac {1}{2}\) (y1 + y2 ) × (x1 – x2)} + {\(\frac {1}{2}\) (y1 + y3 ) × (x3 – x1)} – {\(\frac {1}{2}\) (y2 + y3 ) × (x3 – x2)}
= \(\frac {1}{2}\) {x1 (y1 + y2 – y1 – y3 ) + x2 (y2 + y3 – y1 – y2 ) – x3 (y1 + y3 – y2 – y3 ) }
= \(\frac {1}{2}\) {x1 (y2 – y3 ) + x2 (y3 – y1 ) + x3 (y1 – y2 ) }
10. If the points A (a, 0), B (0, b) and C (c, 0) are collinear then a = -c.
a) False
b) True
View Answer
Explanation: We know that, area of triangle = \(\frac {1}{2}\){x1(y2 – y3 ) + x2(y3 – y1 ) + x3(y1 – y2 )}
The three points are A (a, 0), B (0, b) and C (c, 0)
Since the points are collinear, the area of triangle will be zero.
The area of triangle = \(\frac {1}{2}\) {a(b – 0) + 0(c – 0) + c(0 – b) } = \(\frac {1}{2}\) {ab + 0 – bc}
\(\frac {1}{2}\) {ab – bc} = 0
{ab – bc} = 0
a = c
Sanfoundry Global Education & Learning Series – Mathematics – Class 10.
To practice all chapters and topics of class 10 Mathematics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Practice Class 9 Mathematics MCQs
- Practice Class 8 Mathematics MCQs
- Check Class 10 - Mathematics Books
