Class 10 Maths MCQ – Applications of Trigonometry

This set of Class 10 Maths Chapter 9 Multiple Choice Questions & Answers (MCQs) focuses on “Applications of Trigonometry”. These MCQs are created based on the latest CBSE syllabus and the NCERT curriculum, offering valuable assistance for exam preparation.

1. The distance between two objects can be known using trigonometric ratios.
a) True
b) False
View Answer

2. One of the applications of trigonometry is used for astronomers to find the distance between two planets.
a) False
b) True
View Answer

3. _____ is drawn from the eye of an observer to the targeted object.
a) A parallel line
b) Line of sight
c) Elevation line
d) Depression line
View Answer

4. What happens to the angle of elevation if the height of a tower, the distance between the tower and the observer is doubled?
a) Doubled
b) halved
c) Tripled
d) Remains the same
View Answer

5. The angle of depression is always a/an _____ angle.
a) right
b) obtuse
c) complete
d) acute
View Answer

6. A pole stands vertically on the floor. From a point, it is 120 meters away from the foot of the pole and the angle of elevation is 45° then find the height of the pole.
a) 100 meters
b) 180 meters
c) 120 meters
d) 10 meters
View Answer

Answer: c
Explanation: In the figure, BC is the height of the pole.

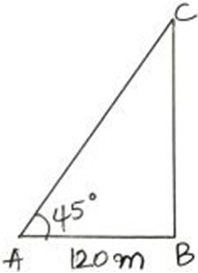
In ∆ABC, Tan 45° = \(\frac {BC}{AB}\)
1 = \(\frac {BC}{AB}\)
1 = \(\frac {BC}{120}\)
BC = 120 meters

7. A slope is built against a wall which makes an angle 30° with the ground and the height of the wall is 2 meters. Find the length of the slope in meters.
a) 2
b) 4
c) 1
d) 3
View Answer

Answer: b
Explanation: AC is the length of the slope in ∆ABC.

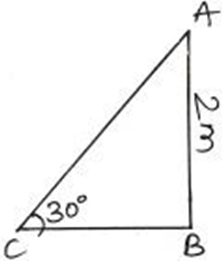
sin 30° = \(\frac {AB}{AC}\)
\( \frac {1}{2} = \frac {2}{AC}\)
AC = 4 meters

8. A slide should be built in a park that has to be set up at 10 meters height and also 10 meters away from the support. What should be the angle of elevation?
a) 45°
b) 30°
c) 60°
d) 90°
View Answer

Answer: a
Explanation: The angle between AC and BC is the angle of elevation that has to be found.

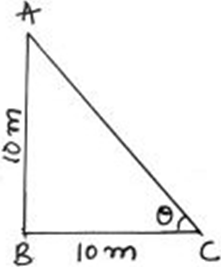
tan⁡ θ = \(\frac {AB}{BC} = \frac {10}{10} \)
Tan θ = 1
θ = 45°

9. A tree trunk of height 12 meters is erected with the support of three metal chains. An angle of 60° is made by each metal chain with the tree trunk. Find the length of the metal chain.
a) 32 meters
b) 10meters
c) 24 meters
d) 18 meters
View Answer

Answer: c
Explanation: We have to find the length of the metal chain AC.

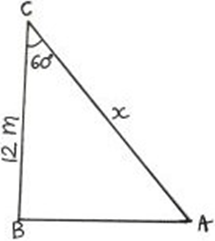
cos 60° = \(\frac {BC}{AC}\)
\( \frac {1}{2} = \frac {12}{AC}\)
AC = 24 meters

10. A ship has to cross a sea by making an angle of 30° and with a distance of 200 meters to reach the shore then find the width of the sea.
a) 300 meters
b) 100 meters
c) 110 meters
d) 50 meters
View Answer

Answer: b
Explanation: The width of the river is BC in the figure.

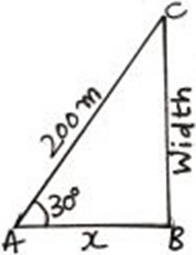
sin 30° = \(\frac {BC}{AC}\)
\( \frac {1}{2} = \frac {BC}{200}\)
BC = 100 meters

To practice all chapters and topics of class 10 Mathematics, here is complete set of 1000+ Multiple Choice Questions and Answers.

If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]