Solution of Quadratic Equation by Squaring Method - Class 10 Maths MCQ

This set of Class 10 Maths Chapter 4 Multiple Choice Questions & Answers (MCQs) focuses on “Solution of Quadratic Equation by Squaring Method”.

1. What are the roots of the equation x²-9x-10?
a) 9, 1
b) -9, -1
c) -10, 1
d) 10, -1
View Answer

Answer: d
Explanation: x²-9x-10=0
Shifting -10 to RHS
x²-9x=10
Adding \(\frac {b^2}{4}\) on both sides, where b=-9
x² – 9x + \(\frac {-9^2}{4} = \frac {-9^2}{4}\) + 10
x² – 9x + \(\frac {81}{4} = \frac {81}{4}\) + 10
x² – 9x + \(\frac {81}{4} = \frac {121}{4}\)
\((x-\frac {9}{2})\)²=\((\frac {11}{2})\)²
x – \(\frac {9}{2}\) = ± \(\frac {11}{2}\)
x = \(\frac {11}{2}+\frac {9}{2}=\frac {20}{2}\) = 10 and x = \(\frac {-11}{2} + \frac {9}{2} = \frac {-2}{2}\) = -1
The roots of the equation are 10 and -1.

2. How many methods are there to find the roots of a quadratic equation?
a) 1
b) 2
c) 3
d) 4
View Answer

Answer: d
Explanation: There are four methods of solving quadratic equations namely, factorization, completing the square method, using quadratic formula and using square roots.

3. A metro travels at the speed of 396 km at a uniform speed. If the speed had been 5 km/hr. more, it would have taken 2 hours less for the same journey. What is the speed of the train?
a) 32 km/hr
b) 30 km/hr
c) 20.06 km/hr
d) 29.06 km/hr
View Answer

Answer: d
Explanation: Let the speed of the metro train be x km/hr
Time taken to cover 396 km at x km/hr = \(\frac {396}{x}\) hrs
Time taken to cover 396 km at x+5 km/hr = \(\frac {396}{x+5}\) hrs
∴ \(\frac {396}{x}-\frac {396}{(x+5)}\)=2
\(\frac {x+5-x}{x(x+5)}=\frac {2}{396}\)
\(\frac {5}{x^2+5x}=\frac {1}{198}\)
990=x²+5x
x²+5x=990
Adding \(\frac {b^2}{4}\) on both sides, where b=5
x² + 5x + \(\frac {5^2}{4}=\frac {5^2}{4}\) + 990
x² + 5x + \(\frac {25}{4}=\frac {25}{4}\) + 990
\((x + \frac {5}{2})\)²=\((\frac {\sqrt {3985}}{2})\)²
x + \(\frac {5}{2}\) = ±\(\frac {\sqrt {3985}}{2}\)
x = \(\frac {63.12}{2} -\frac {5}{2}=\frac {58.12}{2}\) = 29.06 and x = \(\frac {-63.12}{2} -\frac {5}{2} = \frac {-68.12}{2}\) = -34.06
Since, speed cannot be negative hence x=29.06 km/hr

4. The sum of areas of two squares is 625m². If the difference in their perimeter is 20m then, what will be the sides of squares?
a) 10, 15
b) 15.28, 20.28
c) 13, 67.34
d) 35.67, 46.78
View Answer

Answer: b
Explanation: Let the sides of two squares be x and y.
Their areas will be x² and y² respectively.
Sum of their areas is 625 m²
x²+y²=625 (1)
Their perimeters will be 4x and 4y
Difference in their perimeters is 20 m
4x-4y=20
x-y=5
x=5+y (2)
Substituting (2) in (1) we get,
(y+5)²+y²=625
y²+10y+25+y²=625
2y²+10y+25=625
2y²+10y-620=0
y²+5y=310
Adding \(\frac {b^2}{4}\) on both sides, where b=5
y² + 5y + \(\frac {5^2}{4}=\frac {5^2}{4}\) + 310
y² + 5y + \(\frac {25}{4}=\frac {25}{4}\) + 310
y² + 5y + \(\frac {25}{4}=\frac {1265}{4}\)
\((y+\frac {5}{2})\)² = \((\frac {\sqrt {1265}}{2})\)²
y+\(\frac {5}{2}\) = ±\(\frac {\sqrt {1265}}{2}\)=±\(\frac {35.56}{2}\)
y = \(\frac {35.56}{2}-\frac {5}{2}=\frac {30.56}{2}\) = 15.28 and y = \(\frac {-35.56}{2}-\frac {5}{2}=\frac {-40.56}{2}\) = -20.28
Since, length cannot be negative hence, y=15.28
Now, x=5+y=5+15.28=20.28

5. The diagonal of rectangular field is 20 more than the shorter side. If the longer side is 10 more than shorter side what will be the area of the rectangular field?
a) 1000
b) 1100
c) 1200
d) 1500
View Answer

Answer: c
Explanation: Let the length of shorter side be x.
Length of longer side = x+10
Length of diagonal = x+20

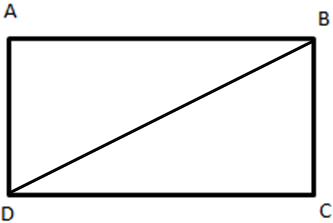
Here, ∆BDC forms a right-angled triangle. Hence by Pythagoras Theorem,
BD²=BC²+DC²
(x+20)²=x²+(x+10)²
x²+40x+400=x²+x²+20x+100
40x+400=x²+20x+100
x²-20x-300=0
x²-20x=300
Adding \(\frac {b^2}{4}\) on both sides, where b=-20
x² – 20x + \(\frac {-20^2}{4}=\frac {-20^2}{4}\) + 300
x² – 20x + \(\frac {400}{4}=\frac {400}{4}\) + 300
x² – 20x + \(\frac {400}{4}=\frac {1600}{4}\)
\((x-\frac {20}{2})\)² = \((\frac {40}{2})\)²
x – \(\frac {20}{2}\) = ±\(\frac {40}{2}\)
x = \(\frac {40}{2}+\frac {20}{2}=\frac {60}{2}\) = 30 and x = \(\frac {-40}{2}+\frac {20}{2}=\frac {-20}{2}\) = -10
Since length cannot be negative, hence x = 30
The length of the other side is x + 10 = 30 + 10 = 40
Area of rectangle = 40 × 30 = 1200 units

Subscribe Now: Class 10 - Mathematics Newsletter | Important Subjects Newsletters

6. A rectangular field is 50 m long and 20 m wide. There is a path of equal width all around it having an area of 121 m². What will be the width of the path?
a) 10.205 m
b) 11.205 m
c) 12.56 m
d) 13.76 m
View Answer

Answer: b
Explanation:

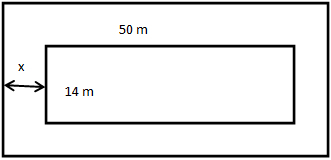
Let the width of the path be x metres.
Length of the field including the path = 50+2x m
Breadth of the field including the path = 14+2x m
Area of the field including the path = (50+2x)(14+2x) m²
Area of the field excluding the path = 50×14=700 m²
∴ area of the path = [(50+2x)(14+2x)]-700
∴ [(50+2x)(14+2x)]-700=121
700+100x+28x+4x²-700=121
4x²+128x-121=0
x²+42x=\(\frac {121}{4}\)
Adding \(\frac {b^2}{4}\) on both sides, where b=42
x² + 42x + \(\frac {42^2}{4}=\frac {42^2}{4}+\frac {121}{4}\)
x² + 42x + \(\frac {1764}{4}=\frac {1764}{4}+\frac {121}{4}\)
x² + 42x + \(\frac {1764}{4}=\frac {1885}{4}\)
\((x+\frac {21}{2})\)²=\((\frac {\sqrt {1885}}{2})\)²
x + \(\frac {21}{2}\) = ±\(\frac {\sqrt {1885}}{2}\) = ±\(\frac {43.41}{2}\)
x = \(\frac {43.41}{2}-\frac {21}{2}=\frac {22.41}{2}\) = 11.205 and x = \(\frac {-43.41}{2}-\frac {21}{2}=\frac {-64.41}{2}\) = -32.20
Since, the length cannot be negative; therefore, x=11.205 m

7. The area of right angled triangle is 500 cm². If the base of the triangle is 10 less than the altitude of the triangle, what are the dimensions of the triangle?
a) base = 32 cm, altitude = 42 cm
b) base = 42 cm, altitude = 62 cm
c) base = 76 cm, altitude = 42 cm
d) base = 32 cm, altitude = 55 cm
View Answer

Answer: a
Explanation: Let the altitude of the triangle be x cm.
The base will be x-10 cm.
The area of triangle is 500 cm²
\(\frac {1}{2}\) × base × altitude = 672
\(\frac {1}{2}\) × (x-10) × x = 672
x²-10x=1344
Adding \(\frac {b^2}{4}\) on both sides, where b=-10
x² – 10x + \(\frac {-10^2}{4}=\frac {-10^2}{4}\) + 1344
x² – 10x + \(\frac {100}{4}=\frac {100}{4}\) + 1344
x² – 10x + \(\frac {100}{4}=\frac {5476}{4}\)
\((x-\frac {10}{2})\)²=\((\frac {74}{2})\)²
x-\(\frac {10}{2}\)=±\(\frac {74}{2}\)
x = \(\frac {74}{2}+\frac {10}{2}=\frac {84}{2}\) = 42 and x = \(\frac {-74}{2}+\frac {10}{2}=\frac {-64}{2}\) = -32
Since, length cannot be negative, hence x=42 cm
Base will be x-10=42-10=32 cm

8. The perimeter of rectangle is 24 cm and area of rectangle is 35cm². What are the dimensions of the rectangle?
a) l=9, b=5
b) l=12, b=5
c) l=5, b=7
d) l=5, b=5
View Answer

Answer: c
Explanation: Let the length of the rectangle be l cm and breadth be b cm.
Perimeter of rectangle = 24
2(l+b)=24
l+b=12
l=12-b (1)
Now, the area of rectangle is 35 cm²
l×b=35 (2)
Substituting (1) in (2)
(12-b)b=35
12b-b²=35
b²-12b+35=0
b²-12b=-35
Adding \(\frac {b^2}{4}\) on both sides, where b=-12
b² – 12b + \(\frac {-12^2}{4}=\frac {-12^2}{4}\) – 35
b² – 12b + \(\frac {144}{4}=\frac {144}{4}\) – 35
b² – 12b + \(\frac {144}{4}=\frac {4}{4}\)
\((b-\frac {12}{2})\)²=\((\frac {2}{2})\)²
b-\(\frac {12}{2}\)=±\(\frac {2}{2}\)
b = \(\frac {2}{2}+\frac {12}{2}=\frac {14}{2}\) = 7 and b = \(\frac {-2}{2}+\frac {12}{2}=\frac {10}{2}\) = 5
The length of the rectangle is l=12-b=12-7=5 and l=12-5=7
The length and breadth of the rectangle are 7 and 5 or 5 and 7.

9. The sum of ages of Eera and her sister is 46 and the product of their ages is 465. What are their ages?
a) Eera 31, Her sister 15
b) Eera 5, Her sister 10
c) Eera 12, Her sister 37
d) Eera 57, Her sister 12
View Answer

Answer: a
Explanation: Let the age of Eera be x years. The age of her sister will be 46-x years.
The product of their ages is 465.
x(46-x)=465
46x-x²=465
x²-46x+465=0
x²-46x=-465
Adding \(\frac {b^2}{4}\) on both sides, where b=-46
x² – 46x + \(\frac {-46^2}{4}=\frac {-46^2}{4}\) – 465
x² – 46x + \(\frac {2116}{4}=\frac {2116}{4}\) – 465
x² – 46x + \(\frac {2116}{4}=\frac {256}{4}\)
\((x-\frac {46}{2})\)²=\((\frac {16}{2})\)²
x-\(\frac {46}{2}\)=±\(\frac {16}{2}\)
x = \(\frac {16}{2}+\frac {46}{2}=\frac {62}{3}\) = 31 and x = \(\frac {-16}{2}+\frac {46}{2}=\frac {30}{2}\) = 15
The ages of Eera and her sister are 31 and 15 respectively or 15 and 31 years.

10. The sum of a number and its square root is 110. What is the number?
a) 100
b) 102
c) 99
d) 98
View Answer

Answer: a
Explanation: Let the number be x. It square root will be √x
Sum of the number and its square root is 110.
x+√x=110
Let √x=y, x=y²
The equation becomes,
y²+y=110
Adding \(\frac {b^2}{4}\) on both sides, where b=1
y² + y + \(\frac {1^2}{4}=\frac {1^2}{4}\) + 110
y² + y + \(\frac {1}{4}=\frac {1}{4}\) + 110
y² + y + \(\frac {1}{4}=\frac {441}{4}\)
\((y+\frac {1}{2})\)² = \((\frac {21}{2})\)²
y + \(\frac {1}{2}\) = ±\(\frac {21}{2}\)
y = \(\frac {21}{2}-\frac {1}{2}=\frac {20}{2}\) = 10 and y = \(\frac {-20}{2}-\frac {1}{2}=\frac {-21}{2}\) = -10.5
x = y² = 10² = 100 and x = y² = -10.5² = 110.25
The numbers are 100 and 110.25.

Sanfoundry Global Education & Learning Series – Mathematics – Class 10.

To practice all chapters and topics of class 10 Mathematics, here is complete set of 1000+ Multiple Choice Questions and Answers.

If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]

« Prev - Class 10 Maths MCQ – Quadratic Equations

» Next - Class 10 Maths MCQ – Quadratic Equations – Determination of Types of Roots

Related Posts:

Recommended Articles: