Class 10 Maths MCQ – Pythagoras Theorem

This set of Class 10 Maths Chapter 6 Multiple Choice Questions & Answers (MCQs) focuses on “Pythagoras Theorem”.

1. ∆ABC is a right angled triangle, where AB = 5cm, BC = 10cm, AC = 15cm.
a) False
b) True
View Answer

2. A man travels A to B, B to C, C to D and then finally D to E. What will be the shortest route the man could have taken?

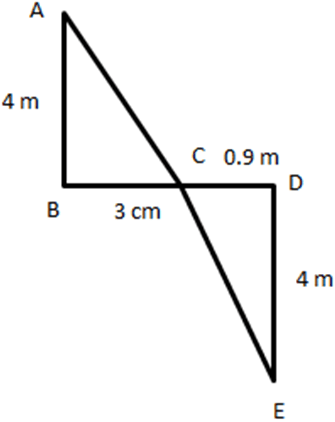
a) 9.3 m
b) 9.2 m
c) 9.1 m
d) 9 m
View Answer

3. What will be the distance of the foot of ladder from the building, if the ladder of 12 m high reaches the top of a building 35 m high from the ground?
a) 32.65 m
b) 32.87 m
c) 31.87 m
d) 32.85 m
View Answer

Answer: b
Explanation:

Here, AB is the building and AC is the ladder.
Now, the BC can be found out by Pythagoras Theorem.
AC² = AB² + BC²
35² = 12² + BC²
1225 = 144 + BC²
BC² = 1225 – 144 = 1081
BC = √1081 = 32.87 m
The distance between the foot of the ladder and the building is 32.87 m.

4. The heights of two vertical lamp posts are 33 m and 24 m high. If the distance between them is 40 m, then what will be the distance between their tops?
a) 47.89m
b) 56.56m
c) 32.81m
d) 41m
View Answer

Answer: d
Explanation:

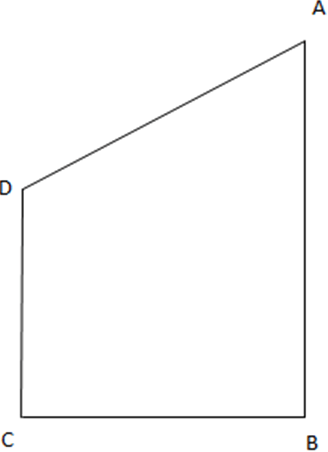
Here, DC and AB are two lampposts of height 24 m and 33 m respectively.
The distance BC is 40m.
Now, draw a line perpendicular to AB from D.

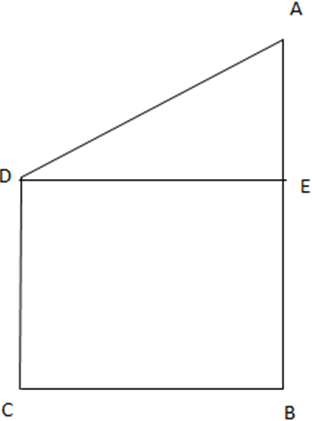
Now, AED is a right-angled triangle, right angled at E.
AB = AE + EB
33 = AE + DC
33 = AE + 24
33 – 24 = AE
AE = 9m
In ∆AED,
AD² = DE² + EA²
AD² = 40² + 9²
AD² = 1600 + 81
AD² = 1681
AD = √1681 = 41 m
The distance between the two lampposts is 41 m.

5. ∆ABC is a right-angled triangle, right angled at B and BD ⊥ AC. If BD = 10cm, AB = 5 cm and BC = 5 cm then AC will be?
a) 44.72 cm
b) 5.59 cm
c) 18.11 cm
d) 22.36 cm
View Answer

Answer: d
Explanation: The figure according to the given data is:

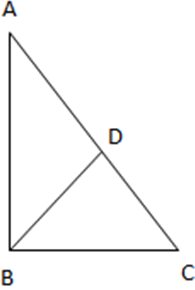
BD = 10cm and AB = 5cm
Now, in ∆ADB
AD² = AB² + BD²
AD² = 5² + 10²
AD² = 25 + 100
AD² = 125
AD = √125 = 11.18 cm
Now, in ∆ABD and ∆CBD
BD = BD     (Common Side)
∠ADB = ∠CDB     (Both 90°)
AB = BC     (Given)
∆ABD ≅ ∆CDB (RHS Congruency)
Therefore, AD = DC
AC = AD + DC = 2AD = 2 × 11.18cm = 22.36cm

6. Which of triangle whose sides are given below are right angled?
a) AB = 89, AC = 80, BC = 39
b) AB = 57, AC = 50, BC = 45
c) AC = 34, AB = 20, BC = 21
d) AC = 50, AB = 32, BC = 20
View Answer

7. The lengths of diagonals of a rhombus are 10 cm and 8 cm. What will be the length of the sides of rhombus?
a) 6.40 cm
b) 5.25 cm
c) 2.44 cm
d) 3.29 cm
View Answer

Answer: a
Explanation:

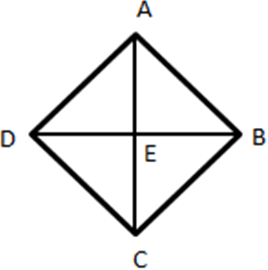
ABCD is a rhombus. The length of diagonal is 10 cm and the length of other diagonal is 8 cm.
Since, diagonals of a rhombus bisect each other. Therefore, AE = 4cm and DE = 5 cm
Now, in ∆AED
AD² = AE² + DE²
AD² = 4² + 5 ²     (Since, AD is the altitude of the triangle it will bisect BC)
AD² = 16 + 25
AD² = 41
AD = √41 cm = 6.40 cm

8. If the side of rhombus is 13 cm and one of its diagonals is 24 cm, then what will be length of the other diagonal?
a) 8.4 cm
b) 4 cm
c) 11 cm
d) 10 cm
View Answer

Answer: d
Explanation:

ABCD is a rhombus. The side of the rhombus is 13 cm and the length of one of its diagonal is 24 cm.
Let the length of other diagonal be 2x cm.
Since, diagonals of a rhombus bisect each other. Therefore, AE = x cm and DE = 12 cm
Now, in ∆AED
AD² = AE² + DE²
13² = x² + 12²     (Since, AD is the altitude of the triangle it will bisect BC)
x² = 169 – 144
x² = 25
x = √25 = 5 cm
AC = 2 × AE = 2 × 5 = 10 cm

9. What will be the length of the altitude of an equilateral triangle whose side is 9 cm?
a) 4.567 cm
b) 7.794 cm
c) 8.765 cm
d) 4.567 cm
View Answer

Answer: b
Explanation:

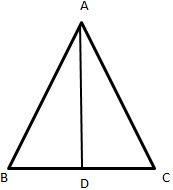
Here, ABC is an equilateral triangle and AD is the altitude of the triangle.
Now, in ∆ADB
AB² = AD² + BD²
9² = AD² + 4.5²     (Since, AD is the altitude of the triangle it will bisect BC)
AD² = 81 – 20.25
AD² = 60.75
AD = √60.75 = \(\frac {9\sqrt {3}}{2}\) cm = 7.794 cm

10. What will be the length of the square inscribed in a circle of radius 5 cm?
a) 2.34 cm
b) 3.45 cm
c) 5√2 cm
d) 2.45 cm
View Answer

Answer: c
Explanation:
The diagram according to the given data is:

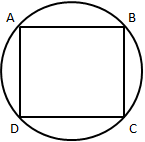
ABCD is a square inscribed in a circle of radius 5 cm.
Now, joining the diagonals of the square we get

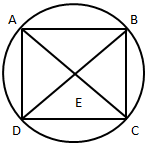
The diagonals intersect at E. We know that the diagonals of square are perpendicular to each other.
In ∆AED, using Pythagoras Theorem,
AD² = DE² + AE²
DE and EA are the radius of the circle, ∴ DE = EA
AD² = 2DE²
AD² = 2 × 5² = 2 × 25 = 50
AD² = 50
AD² = 125
AD = √50 = 5√2 cm

Sanfoundry Global Education & Learning Series – Mathematics – Class 10.

To practice all chapters and topics of class 10 Mathematics, here is complete set of 1000+ Multiple Choice Questions and Answers.

If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]