This set of Class 10 Maths Chapter 2 Multiple Choice Questions & Answers (MCQs) focuses on “Polynomials”. These MCQs are created based on the latest CBSE syllabus and the NCERT curriculum, offering valuable assistance for exam preparation.
1. The graph of the polynomial 4x2-8x+3 cuts the x-axis at ________ and ________ points.
a) (\(\frac {3}{4}\), 0), (\(\frac {1}{2}\), 0)
b) (\(\frac {3}{2}\), 0), (\(\frac {1}{2}\), 0)
c) (\(\frac {3}{2}\), 0), (\(\frac {1}{6}\), 0)
d) (\(\frac {7}{2}\), 0), (\(\frac {3}{2}\), 0)
View Answer
Explanation: The graph of the polynomial cuts the x-axis. Only the zeros of the polynomial cut the x-axis.
4x2-8x+3=0
4x2-6x-2x+3=0
2x(2x-3)-1(2x-3)=0
(2x-3)(2x-1)=0
x=\(\frac {3}{2}, \frac {1}{2}\)
Hence, the graph of the polynomial cuts the x-axis at (\(\frac {3}{2}\), 0) and (\(\frac {1}{2}\), 0).
2. The graph of the polynomial 2x2-8x+5 cuts the y-axis at __________
a) (6, 0)
b) (0, 7)
c) (0, 5)
d) (8, 9)
View Answer
Explanation: The graph of the polynomial 2x2-8x+5 cuts the y-axis.
Hence, the value of x will be 0.
y(0)=2(0)2-8(0)+5
y=5
The graph cuts the y-axis at (0,5)
3. How many points will the graph of x2+2x+1 will cut the x-axis?
a) 3
b) 1
c) 2
d) 0
View Answer
Explanation: The graph of x2+2x+1 does not cut the x-axis, because it has imaginary roots.
x2+2x+1=0
x2+x+x+1=0
x(x+1)+(x+1)=0
(x+1)(x+1)=0
x=-1, -1
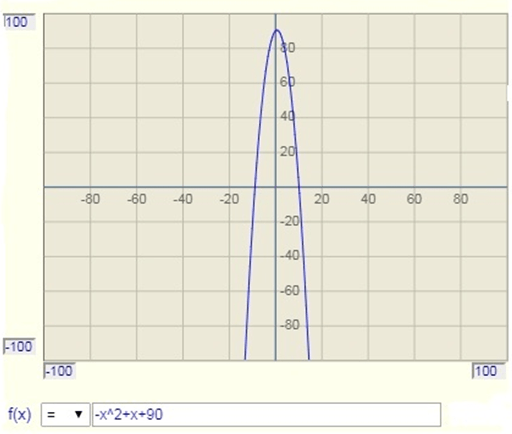
4. The graph of the quadratic polynomial -x2+x+90 will open upwards.
a) False
b) True
View Answer
Explanation: The graph of the polynomial will have a downward opening since, a<0
The graph for the same can be observed here,
5. If the graph of a polynomial cuts the x-axis at 3 points, then the polynomial is ______
a) Linear
b) Quadratic
c) Cubic
d) Biquadratic
View Answer
Explanation: Since, the graph of the polynomial cuts the x-axis at 3 points, hence, it will be a cubic polynomial. A polynomial is said to be linear, quadratic, cubic or biquadratic according to the degree of the polynomial.
6. What will be the nature of the zeros of a quadratic polynomial if it cuts the x-axis at two different points?
a) Real
b) Distinct
c) Real, Distinct
d) Complex
View Answer
Explanation: The zeros of the quadratic polynomial cut the x-axis at two different points.
∴ b2 – 4ac ≥ 0
Hence, the nature of the zeros will be real and distinct.
7. The graph of a quadratic polynomial cuts the x-axis at only one point. Hence, the zeros of the quadratic polynomial are equal and real.
a) True
b) False
View Answer
Explanation: If the graph meets x-axis at one point only, then the quadratic polynomial has coincident zeros. Also, the discriminant of the quadratic polynomial is zero, therefore roots will be real.
8. A real number is called zeros of the polynomial p(x) if _________
a) p(α)=4
b) p(α)=1
c) p(α)≠0
d) p(α)=0
View Answer
Explanation: A number is called zero of polynomial when it satisfies the equation of the polynomial.
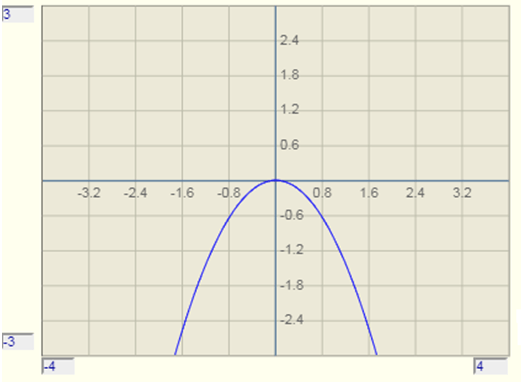
9. If a < 0, then the graph of ax2+bx+c, has a downward opening.
a) True
b) False
View Answer
Explanation: The leading coefficient of the polynomial is less than zero, hence, it has downward opening. For example, the graph of -x2 is
10. A polynomial is said to be linear, quadratic, cubic or biquadratic according to the degree of the polynomial.
a) False
b) True
View Answer
Explanation: The degree of the polynomial is the highest of the degree of the polynomial. Hence, a polynomial with highest degree one is linear, two as quadratic and so on.
11. Which of the following is a polynomial?
a) x2+2x+5
b) √x+2x+4
c) x\(\frac {2}{3}\)+10x
d) 5x+\(\frac {5}{x}\)
View Answer
Explanation: An expression in the form of (x)=a0+a1x+a2x2+…+anxn, where an≠0, is called a polynomial where a1, a2 … an are real numbers and each power of x is a non-negative integer.
In case of √x+2x+4 , the power of √x is not an integer. Similarly for x\(\frac {2}{3}\)+10x, \(\frac {2}{3}\) is a fraction.
Now, 5x+\(\frac {5}{x}\) in this case the power of x is a negative integer. Hence it is not a polynomial.
12. The biquadratic polynomial from the following is ______
a) (x2+3)(x2-3)
b) x2-7
c) x7+x6+x5
d) 5x-3
View Answer
Explanation: A biquadratic polynomial has highest power 4.
Hence, the polynomial with the highest power as 4 is x4-9 or (x2+3)(x2-3).
13. Which of the following is not a polynomial?
a) x2+5x+10
b) √x+2x+4
c) x10+10x
d) 5x+4
View Answer
Explanation: An expression in the form of (x)=a0+a1x+a2x2+…+anxn, where an≠0, is called a polynomial where a1, a2 … an are real numbers and each power of x is a non-negative integer.
In case of √x+2x+4, the power of x is not an integer.
Therefore it is not a polynomial.
14. If the zeros of a polynomial are 3 and -5, then they cut the x-axis at ____ and _____ points.
a) (8, 0) and (-4, 0)
b) (3, -3) and (-5, 5)
c) (-3, 0) and (5, 0)
d) (3, 0) and (-5, 0)
View Answer
Explanation: Since, the zeros of the polynomial are 3 and -5.
Therefore, x = 3 and x = -5 and they cut the x-axis so the y-coordinate will be zero.
Hence, the points it cuts the x-axis will be (3, 0) and (-5, 0).
15. If the graph of the quadratic polynomial is completely above or below the x-axis, then the nature of roots of the polynomial is _____
a) Real and Distinct
b) Distinct
c) Real
d) Complex
View Answer
Explanation: Since, the graph is completely above or below the x-axis, hence, it has no real roots. If a polynomial has real roots only then it cuts the x-axis. If it lies above or below, the roots are complex in nature.
More MCQs on Class 10 Maths Chapter 2:
- Chapter 2 – Polynomials MCQ (Set 2)
- Chapter 2 – Polynomials MCQ (Set 3)
- Chapter 2 – Polynomials MCQ (Set 4)
To practice all chapters and topics of class 10 Mathematics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Practice Class 8 Mathematics MCQs
- Practice Class 9 Mathematics MCQs
- Check Class 10 - Mathematics Books
