This set of Class 10 Maths Chapter 7 Multiple Choice Questions & Answers (MCQs) focuses on “Coordinate Geometry”. These MCQs are created based on the latest CBSE syllabus and the NCERT curriculum, offering valuable assistance for exam preparation.
1. What will be the coordinates of the point which divides the line segment joining the points A(-2, 2) and B(-1, 5) in the ratio 2:5?
a) (\(\frac {-4}{3}, \frac {-20}{9}\))
b) (\(\frac {-4}{3}, \frac {20}{9}\))
c) (\(\frac {4}{3}, \frac {20}{9}\))
d) (\(\frac {4}{3}, \frac {-20}{9}\))
View Answer
Explanation: Using, section formula x = \(\frac {mx_2+nx_1}{m+n}\) and y = \(\frac {my_2+ny_1}{m+n}\)
The points are A(-2, 2) and B(-1, 5) and the ratio is 2:5
∴ x = \(\frac {2(-1)+5(-2)}{2+7} = \frac {-2-10}{9} = \frac {-12}{9} = \frac {-4}{3}\)
y = \(\frac {2(5)+5(2)}{2+7} = \frac {10+10}{9} = \frac {20}{9} = \frac {20}{9}\)
Hence, the point is (\(\frac {-4}{3}, \frac {20}{9}\)).
2. What will be the coordinates of the midpoint of the line segment joining the points (-5, 10) and(15, 2)?
a) (-5, -6)
b) (-5, 6)
c) (5, 6)
d) (5, -6)
View Answer
Explanation: Midpoint lies in the center of the line segment
Hence, it divides the line in the ratio 1:1
Using, section formula x = \(\frac {mx_2+nx_1}{m+n}\) and y = \(\frac {my_2+ny_1}{m+n}\)
The points are A(-5, 10) and B(15, 2) and the ratio is 1:1
∴ x = \(\frac {1(-5)+1(15)}{2} = \frac {-5+15}{2} = \frac {10}{2}\) = 5
y = \(\frac {1(2)+1(10)}{2} = \frac {2+10}{2} = \frac {12}{2}\) = 6
Hence, the point is (5,6).
3. In what ratio does the point (\(\frac {-19}{3}, \frac {7}{3}\)) divide the line segment joining A(3, 7) and B(-11, 0)?
a) 1:2 (externally)
b) 1:2 (internally)
c) 2:1 (externally)
d) 2:1 (internally)
View Answer
Explanation: Let the ratio in which the point (\(\frac {-19}{3}, \frac {7}{3}\)) divides the line segment joining the points A(3, 7) and B(-11, 0) be k:1
Using, section formula x = \(\frac {mx_2+nx_1}{m+n}\) and y = \(\frac {my_2+ny_1}{m+n}\)
The points are A(3, 7) and B(-11, 0) and the ratio is k:1
∴ x = \(\frac {k(-11)+1(3)}{k+1} = \frac {-11k+3}{k+1}\)
y = \(\frac {k(0)+1(7)}{k+1} = \frac {7}{k+1}\)
Since, the point is (\(\frac {-19}{3}, \frac {7}{3}\)).
∴ \(\frac {-19}{3} = \frac {-11k+3}{k+1}\)
-19(k + 1) = 3(-11k + 3)
-19k – 19 = -33k + 9
-19k + 33k = 19 + 9
14k = 28
k = \(\frac {28}{14}\) = 2
The ratio is 2:1.
4. What will be the value of y, if the ratio in which the point (\(\frac {3}{4}\), y) divides the line segment joining the points A(-1, 4) and B(6, 5)is 1:3?
a) y = \(\frac {9}{2}\)
b) y = \(\frac {5}{2}\)
c) y = \(\frac {9}{4}\)
d) y = \(\frac {5}{2}\)
View Answer
Explanation: Using, section formula x = \(\frac {mx_2+nx_1}{m+n}\) and y = \(\frac {my_2+ny_1}{m+n}\)
The points are (-1, 4)and B(6, 5)in the ratio 1:3
∴ x = \(\frac {1(6)+3(-1)}{1+3} = \frac {6-3}{4} = \frac {3}{4}\)
y = \(\frac {1(6)+3(4)}{1+3} = \frac {6+12}{4} = \frac {18}{4}\)
Therefore y = \(\frac {9}{2}\)
5. What will be ratio in which the line 3x + y – 11 = 0 divides the line segment joining the points (0, -1) and (-3, -4)?
a) 1:2 (internally)
b) 1:2 (externally)
c) 2:1 (externally)
d) 2:1 (internally)
View Answer
Explanation: Let the ratio in which the line 3x + y – 11 = 0 divides the line segment joining the points (0, -1) and (-3, -4) be k:1.
Using, section formula x = \(\frac {mx_2+nx_1}{m+n}\) and y = \(\frac {my_2+ny_1}{m+n}\)
The points are A(0, -1) and B(-3, -4) and the ratio is k:1.
∴ x = \(\frac {k(-3)+1(0)}{k+1} = \frac {-3k}{k+1}\)
y = \(\frac {k(-4)+1(-1)}{k+1} = \frac {-4k-1}{k+1}\)
Since, the point \((\frac {-3k}{k+1}, \frac {-4k-1}{k+1} )\) lies on the line 3x+y-11 = 0.
3 \((\frac {-3k}{k+1} + \frac {-4k-1}{k+1} )\)-11 = 0
3(-3k) + (-4k – 1) – 11(k + 1) = 0
-9k – 4k – 1 – 11k – 11 = 0
-24k – 12 = 0
-24k = 12
k = \(\frac {12}{-24} = \frac {-1}{2}\)
The ratio is 1:2 (externally).
6. In what ratio is the line segment joining the points A(-5, 2) and B(3, 9) divided by the x-axis?
a) 2:5 (internally)
b) 2:5 (externally)
c) 2:9 (externally)
d) 2:9 (internally)
View Answer
Explanation: Let the ratio in which the x-axis divides the line segment joining the points A(-5, 2) and B(3, 9) be k:1
Using, section formula x = \(\frac {mx_2+nx_1}{m+n}\) and y = \(\frac {my_2+ny_1}{m+n}\)
The points are A(-5, 2) and B(3, 9) and the ratio is k:1
∴ x = \(\frac {k(3)+1(-5)}{k+1} = \frac {3k-5}{k+1}\)
y = \(\frac {k(9)+1(2)}{k+1} = \frac {9k+2}{k+1}\)
Since, the point is on x-axis.
Hence, the y-coordinate will be zero.
∴ 0 = \(\frac {9k+2}{k+1}\)
0 = 9k+2
k = \(\frac {-2}{9}\)
The ratio in which the y-axis cuts the line segment joining the points A(-5, 2) and B(3, 9) will be 2:9 (externally).
7. In what ratio is the line segment joining the points A(2, 4) and B(6, 5) divided by the y-axis?
a) 2:1 (internally)
b) 2:1 (externally)
c) 3:1 (internally)
d) 3:1 (externally)
View Answer
Explanation: Let the ratio in which the y-axis divides the line segment joining the points A(2, 4) and B(6, 5) be k:1
Using, section formula x = \(\frac {mx_2+nx_1}{m+n}\) and y = \(\frac {my_2+ny_1}{m+n}\)
The points are A(2, 4) and B(6, 5) and the ratio is k:1
∴ x = \(\frac {k(6)+1(2)}{k+1} = \frac {6k+2}{k+1}\)
y = \(\frac {k(5)+1(4)}{k+1} = \frac {5k+4}{k+1}\)
Since, the point is on y-axis.
Hence, the x-coordinate will be zero.
∴ 0 = \(\frac {6k+2}{k+1}\)
0 = 6k + 2
k = \(\frac {-6}{2}\) = -3
The ratio in which the y-axis cuts the line segment joining the points A(2, 4) and B(6, 5) will be 3:1 (externally).
8. What will be the coordinates of B, if the point C\((\frac {29}{7}, \frac {46}{7} )\), divides the line segment joining A (5, 8) and B (a, b) in the ratio 2:5?
a) a = 2, b = 3
b) a = -2, b = 3
c) a = 2, b = -3
d) a = -2, b = -3
View Answer
Explanation: Using, section formula x = \(\frac {mx_2+nx_1}{m+n}\) and y = \(\frac {my_2+ny_1}{m+n}\)
The points are A(5, 8)and B(a, b)in the ratio 2:5
∴ x = \(\frac {2(a)+5(5)}{2+5} = \frac {2a+25}{7}\)
y = \(\frac {2(b)+5(8)}{2+5} = \frac {2b+40}{7}\)
But the coordinates of C are \((\frac {29}{7}, \frac {46}{7} )\)
Therefore, \(\frac {2a+25}{7} = \frac {29}{7}\)
a = 2
\(\frac {2b+40}{7} = \frac {46}{7}\)
b = 3
9. What will be the length of the median through the vertex A, if the coordinates of the vertices of ∆ABC are A(2, 5), B(5, 0), C(-2, 5)?
a) \(\sqrt {\frac {113}{3}}\) units
b) \(\sqrt {\frac {13}{2}}\) units
c) \(\sqrt {\frac {113}{2}}\) units
d) \(\sqrt {\frac {13}{2}}\) units
View Answer
Explanation:
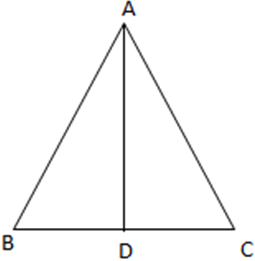
The median through A will bisect the line BC.
Hence, D is the midpoint of BC
Coordinates of D = \((\frac {x_1+x_2}{2}, \frac {y_1+y_2}{2} ) = ( \frac {5-2}{2}, \frac {0-5}{2} ) =( \frac {3}{2}, \frac {-5}{2} )\)
Distance between A and D = \( \sqrt {(x_2-x_1)^2 + (y_2-y_1)^2} \)
= \( \sqrt {(2-\frac {3}{2})^2+ (5+\frac {5}{2})^2} \)
= \( \sqrt {(\frac {1}{2})^2+ (\frac {15}{2})^2} \)
= \( \sqrt {\frac {1}{4}+ \frac {225}{4}} \)
= \( \sqrt {\frac {113}{2}} \) units
10. What will be the coordinates of the fourth vertex S, if P(-1, -1), Q(2, 0), R(2, 3) are the three vertices of a parallelogram?
a) (-5, -12)
b) (5, -12)
c) (5, 12)
d) (-5, 12)
View Answer
Explanation:
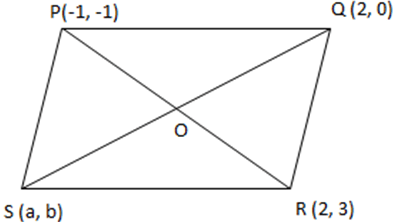
PQRS is a parallelogram. The opposite side of the parallelogram is equal and parallelogram. Also, the diagonals of the parallelogram bisect each other.
∴ O is the mid-point SQ and PR.
Midpoint of PR
Using, section formula x = \(\frac {mx_2+nx_1}{m+n}\) and y = \(\frac {my_2+ny_1}{m+n}\)
The points are P(-1, -1) and R(2, 3) and the ratio is 1:1
∴ x = \(\frac {1(-1)+1(2)}{2} = \frac {-1+2}{2} = \frac {1}{2}\)
y = \(\frac {1(3)+1(-1)}{2} = \frac {3-1}{2} = \frac {2}{2}\) = 1
Hence, the coordinates of O is (5, 6)
Midpoint of QS
Using, section formula x = \(\frac {mx_2+nx_1}{m+n}\) and y = \(\frac {my_2+ny_1}{m+n}\)
The points are Q(2, 0) and S(a, b) and the ratio is 1:1
∴ x = \(\frac {1(a)+1(2)}{2} = \frac {a+2}{2}\)
y = \(\frac {1(b)+1(0)}{2} = \frac {b}{2}\)
The coordinates of O is (5, 6)
Therefore, \(\frac {a+2}{2}\) = 5
a = 8
\(\frac {b}{2}\) = 6, b = 12
The coordinates of S are (5, 12).
11. What will be the value of a and b, if (-5, a), (-3, -3), (-b, 0) and (-3, 3) are the vertices of the parallelogram?
a) a = 0, b = -1
b) a = -1, b = 1
c) a = 1, b = 1
d) a = 0, b = 1
View Answer
Explanation:
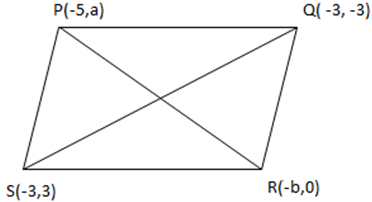
PQRS is a parallelogram. The opposite side of the parallelogram is equal and parallelogram. Also, the diagonals of the parallelogram bisect each other.
∴ O is the mid-point SQ and PR.
Midpoint of PR
Using, section formula x = \(\frac {mx_2+nx_1}{m+n}\) and y = \(\frac {my_2+ny_1}{m+n}\)
The points are P(-5, a) and R(-b, 0) and the ratio is 1:1
∴ x = \(\frac {1(-b)+1(-5)}{2} = \frac {-b-5}{2}\)
y = \(\frac {1(0)+1(a)}{2} = \frac {a}{2}\)
Midpoint of QS
Using, section formula x = \(\frac {mx_2+nx_1}{m+n}\) and y = \(\frac {my_2+ny_1}{m+n}\)
The points are Q(-3, -3) and S(-3, 3) and the ratio is 1:1
∴ x = \(\frac {1(-3)+1(-3)}{2} = \frac {-6}{2}\) = -3
y = \(\frac {1(3)+1(-3)}{2} = \frac {0}{2}\) = 0
Therefore, \(\frac {-b-5}{2}\) = -3
b = 1
\(\frac {a}{2}\) = 0
a = 0
12. What will be the centroid of the ∆ABC whose vertices are A(-2, 4), B(0, 0) and C(4, 2)?
a) (\(\frac {2}{3}\), 2)
b) (\(\frac {2}{3}\), 1)
c) (\(\frac {2}{5}\), 2)
d) (\(\frac {1}{3}\), 2)
View Answer
Explanation: We know, xcentroid = \(\frac {x_1+x_2+x_3}{3}\) and ycentroid = \(\frac {y_1+y_2+y_3}{3}\)
xcentroid = \(\frac {-2+0+4}{3} = \frac {2}{3}\)
ycentroid = \(\frac {4+0+2}{3}\) = 2
The coordinates of the centroid are (\(\frac {2}{3}\), 2).
13. The coordinates of one end of the diameter AB of a circle are A (-2, -3) and the coordinates of diameter are (-2, 0). What will be the coordinates of B?
a) (2, -3)
b) (-2, 3)
c) (2, 3)
d) (-2, -3)
View Answer
Explanation: We know that the diameter is twice the radius.
Hence, the center is the midpoint of the diameter.
Using, section formula x = \(\frac {mx_2+nx_1}{m+n}\) and y = \(\frac {my_2+ny_1}{m+n}\)
The points are A(-2, -3) and center is (-2, 0) and the ratio is 1:1
Let the coordinates of other side of the radius be (x, y).
∴ -2 = \(\frac {1(-2)+1(x)}{2} = \frac {-2+x}{2}\)
-4 = -2 + x
-4 + 2 = x
x = -2
0 = \(\frac {1(-3)+1(y)}{2} = \frac {-3+y}{2}\)
0 = -3 + y
y = 3
Hence, the point is (-2, 3).
14. The coordinates of the ends of the diameter AB of a circle are A (-4, 7) and B(4, 7). What will be the coordinates of the center of the circle?
a) (0, -8)
b) (0, 8)
c) (0, 7)
d) (0, -7)
View Answer
Explanation: We know that the diameter is twice the radius.
Hence, the center is the midpoint of the diameter.
Using, section formula x = \(\frac {mx_2+nx_1}{m+n}\) and y = \(\frac {my_2+ny_1}{m+n}\)
The points are A(-4, 7) and B(4, 7) and the ratio is 1:1
∴ x = \(\frac {1(-4)+1(4)}{2} = \frac {0}{2}\) = 0
y = \(\frac {1(7)+1(7)}{2} = \frac {7+7}{2} = \frac {14}{2}\) = 7
Hence, the point is (0, 7).
15. The two vertices of ∆ABC are given by A(-3, 0) and B(-8, 5) and its centroid is (-2, 1).What will be the coordinates of the third vertex C?
a) (-5, -2)
b) (5, 2)
c) (-5, 2)
d) (5, -2)
View Answer
Explanation: The two vertices of triangle are A (-3, 0) and B (-8, 5). Its centroid is (-2, 1).
We know, xcentroid = \(\frac {x_1+x_2+x_3}{3}\) and ycentroid = \(\frac {y_1+y_2+y_3}{3}\)
Now, xcentroid = \(\frac {-3-8+x_3}{3}\)
xcentroid = -2
-2 = \(\frac {-3 – 8 + x_3}{3}\)
-6 = -3 – 8 + x3
5 = x3
Now, ycentroid = \(\frac {0+5+y_3}{3}\)
ycentroid = 1
1 = \(\frac {0 + 5 + y_3}{3}\)
3 = 5 + y3
-2 = y3
The third coordinate is (5, -2).
More MCQs on Class 10 Maths Chapter 7:
To practice all chapters and topics of class 10 Mathematics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Practice Class 8 Mathematics MCQs
- Practice Class 9 Mathematics MCQs
- Check Class 10 - Mathematics Books
