Class 10 Maths Chapter 8 Trigonometry MCQ

This set of Class 10 Maths Chapter 8 Multiple Choice Questions & Answers (MCQs) focuses on “Trigonometry”. These MCQs are created based on the latest CBSE syllabus and the NCERT curriculum, offering valuable assistance for exam preparation.

1. If sin (A + B) = \(\frac {\sqrt {3}}{2}\) and tan (A – B) = 1. What are the values of A and B?
a) 37, 54
b) 35.7, 40.7
c) 50, 10
d) 52.5, 7.5
View Answer

Answer: d
Explanation: The value of sin (A + B) = \(\frac {\sqrt {3}}{2}\) and sin 60° = \(\frac {\sqrt {3}}{2}\)
∴ A + B = 60 (1)
The value of tan (A – B) = 1 and tan 45° = 1
∴ A – B = 45 (2)
Adding equation (1) and (2)
A + B = 60
+ A – B = 45
– – – – – – – – – – – – –
2 A = 105
A = 52.5
∴ B = 7.5

2. If cos θ = \(\frac {3}{4}\) then value of cos 2θ is ___________
a) \(\frac {1}{6}\)
b) \(\frac {1}{4}\)
c) \(\frac {1}{8}\)
d) \(\frac {3}{8}\)
View Answer

Answer: c
Explanation: cos 2θ = 2cos θ² – 1
cos θ = \(\frac {3}{4}\)
cos 2θ = 2(\(\frac {3}{4}\))² – 1
= \(\frac {1}{8}\)

3. If sin A = \(\frac {8}{17}\), what will be the value of cos A sec A?
a) 2
b) -1
c) 1
d) 0
View Answer

Answer: c
Explanation: sin A = \(\frac {8}{17}\)
cos A sec A can be written as cos⁡A × \(\frac {1}{sec⁡A}\) = 1
∴ cos A sec A = 1

4. The value of each of the trigonometric ratios of an angle depends on the size of the triangle and does not depend on the angle.
a) True
b) False
View Answer

Answer: b
Explanation:

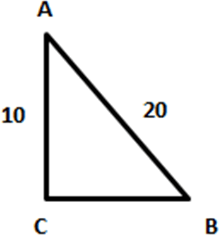
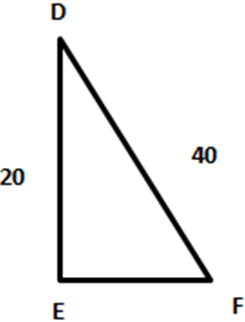
Consider, two triangles ABC and DEF
In ∆ABC,
sin B = \(\frac {AC}{AB} = \frac {10}{20} = \frac {1}{2}\) i.e. B = 30°
Now, in ∆DEF,
sin F = \(\frac {DE}{DF} = \frac {20}{40} = \frac {1}{2}\) i.e. F = 30°
From these examples it is evident that the value of the trigonometric ratios depends on their angle and not on their lengths.

5. If tan α = √3 and cosec β = 1, then the value of α – β?
a) -30°
b) 30°
c) 90°
d) 60°
View Answer

Answer: a
Explanation: tan α = √3 and tan 60° = √3
∴ α = 60°
Cosec β = 1 and cosec 90° = 1
∴ β = 90°
α – β = 60 – 90 = -30°

Sanfoundry Certification Contest of the Month is Live. 100+ Subjects. Participate Now!

6. In triangle ABC, right angled at C, then the value of cosec (A + B) is __________
a) 2
b) 0
c) 1
d) ∞
View Answer

Answer: c
Explanation:
Since the triangle is right angles at C,
The sum of the remaining two angles will be 90
∴ cosec(A + B) = Cosec 90° = 1

7. If tan θ = \(\frac {3}{4}\) then the value of sinθ is _________
a) \(\frac {3}{5}\)
b) \(\frac {4}{4}\)
c) \(\frac {3}{4}\)
d) \(\frac {-3}{5}\)
View Answer

Answer: a
Explanation:

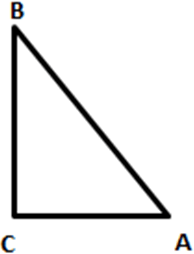
tanθ = \(\frac {BC}{AC} = \frac {3}{4} = \frac {3k}{4k}\)
Hence, BC = 3k, AC = 4k
Using Pythagoras theorem
AB² = AC² + BC²
AB² = 4k² + 3k²
AB = 5k
sinθ = \(\frac {BC}{AB} = \frac {3k}{5k} = \frac {3}{5}\)

8. What is the value of sin30°cos15° + cos30°sin15°?
a) \(\frac {1}{2}\)
b) 0
c) 1
d) \(\frac {1}{\sqrt {2}}\)
View Answer

Answer: d
Explanation:
sin30°cos15° + cos30°sin15° = sin⁡45° = \(\frac {1}{\sqrt {2}}\)

9. What is the value of cos A sec A + sin A cosec A – tan A cot A?
a) 0
b) 2
c) 1
d) 3
View Answer

Answer: c
Explanation:
Cos A sec A = 1
Similarly sin A cosec A = 1 and tan A cot A = 1
∴ cos A sec A + sin A cosec A – tan A cot A = 1 + 1 – 1 = 1

10. In a right angled triangle, the trigonometric function that is equal to the ratio of the side opposite a given angle to the hypotenuse is called cosine.
a) False
b) True
View Answer

Answer: a
Explanation: