Criteria for Similarity of Triangle - Class 10 Maths MCQ

This set of Class 10 Maths Chapter 6 Multiple Choice Questions & Answers (MCQs) focuses on “Criteria for Similarity of Triangle”.

1. In the given figure DE∥BC, if AD = 5.9cm, DB = 4cm and AE = 7cm then, what will be the value of AC?

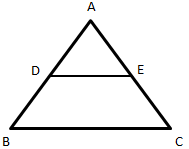
a) 2.3 cm
b) 5.1 cm
c) 11.74 cm
d) 10.9 cm
View Answer

Answer: c
Explanation: In ∆ABC DE∥BC, by Thales Theorem,
∴ \(\frac {AD}{DB}=\frac {AE}{EC}\)
\(\frac {5.9}{4}=\frac {7}{EC}\)
EC = \(\frac {7\times4}{5.9}\) = 4.74 cm
AC = EC + AE = 7 + 4.74 = 11.74 cm

2. What is the value of x?

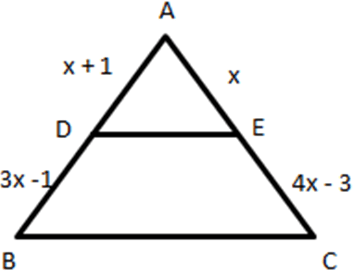
a) 0
b) 1
c) 2
d) 3
View Answer

Answer: b
Explanation: In ∆ABC DE∥BC, by Thales Theorem,
∴ \(\frac {AD}{DB}=\frac {AE}{EC}\)
\(\frac {x + 1}{3x – 1}=\frac {x}{4x – 3}\)
(x + 1)(4x – 3) = x(3x – 1)
4x² – 3x + 4x – 3 = 3x² – x
x² + 2x – 3 = 0
x² + 3x – x – 3 = 0
x(x + 3) – 1(x + 3) = 0
(x + 3)(x – 1) = 0
x = -3, 1
Since lengths cannot be negative so x = 1

3. In ∆PQR, PS is the bisector of ∠P. If PQ = 6.4cm, PR = 14cm, QS = 6cm. What will be the length of PS and QR?

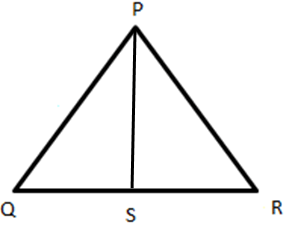
a) 10.5 cm
b) 12.74 cm
c) 10.74 cm
d) 11.74 cm
View Answer

Answer: d
Explanation: In ∆ABC DE∥BC, by Thales Theorem,
∴ \(\frac {AD}{DB}=\frac {AE}{EC}\)
\(\frac {5.9}{4}=\frac {7}{EC}\)
EC = \(\frac {7\times4}{5.9}\) = 4.74cm
AC = EC + AE = 7 + 4.74 = 11.74 cm

4. The perimeters of two similar triangles ABC, PQR is 64 cm and 24 cm respectively. If PQ is 12 cm what will be the length of AB?
a) 30 cm
b) 32 cm
c) 12 cm
d) 16 cm
View Answer

Answer: b
Explanation: We know that the ratio of the perimeters of similar triangles is the same as the ratio of their corresponding sides.
∴ \(\frac {Perimeter \, of \, \triangle ABC}{Perimeter \, of \, \triangle PQR} = \frac {AB}{PQ}\)
\(\frac {64}{24}=\frac {AB}{12}\)
AB = \(\frac {64\times 12}{24}\) = 32 cm

5. In the given figure, LM∥PQ, what will be the relation between x, a, b and c?

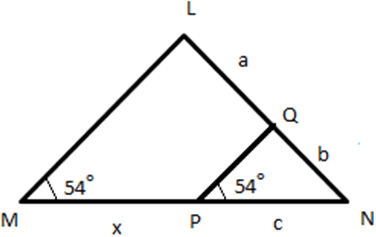
a) a = \(\frac {c}{b}\)
b) ab = cx
c) bx = ac
d) cb = ax
View Answer

Answer: c
Explanation: LM∥PQ by Thales Theorem,
\(\frac {PN}{PM}=\frac {QN}{QL}\)
\(\frac {c}{x}=\frac {b}{a}\)
bx = ac

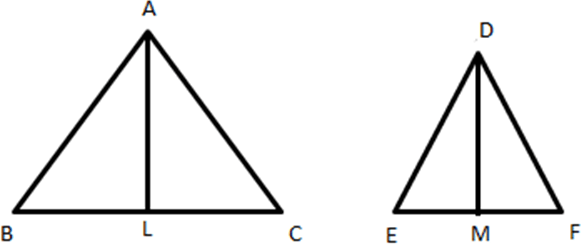
Sanfoundry Certification Contest of the Month is Live. 100+ Subjects. Participate Now!

6. In two similar triangles ∆ABC and ∆DEF, AB = 15cm, DE = 5cm. If AL and DM are the altitudes of the triangles ABC, DEF respectively, then what will be the ratio of their altitudes?

a) 3 : 1
b) 1 : 3
c) 1 : 2
d) 2 : 1
View Answer

Answer: a
Explanation: We know that, if two triangles are equiangular, then the ratio of their corresponding sides is the same as the ratio of their corresponding altitudes.
Since, ∆ABC ∼ ∆DEF therefore, the corresponding angles will be equal.
∴ \(\frac {AB}{DE}=\frac {AL}{DM}\)
\(\frac {15}{5}=\frac {AL}{DM}\)
\(\frac {3}{1}=\frac {AL}{DM}\)

7. If DE∥BC, AD = 4cm, BD = 7.5cm, AE = 6.4 cm & DE = 5cm then what will be the lengths of AC and BC?

a) 11.23 cm
b) 15.24 cm
c) 14.37 cm
d) 14.25 cm
View Answer

Answer: c
Explanation: In ∆ABC DE∥BC, by Thales Theorem,
∴ \(\frac {AD}{DB}=\frac {AE}{EC}\)
\(\frac {4}{7}=\frac {6.4}{EC}\)
EC = \(\frac {7\times 6.4}{4}\) = 11.2 cm
AC = AE + EC = 6.4 + 11.2 = 17.6cm
Also, in ∆ABC and ∆ADE,
∠A = ∠D (Common angle)
∠AEB = ∠ACB (Corresponding angles)
∴ ∆ABC ∼ ∆ADE (AA similarity)
∴ \(\frac {AD}{AB}=\frac {DE}{BC}\)
\(\frac {4}{7.5 + 4} = \frac {5}{BC}\)
BC = \(\frac {11.5\times 5}{4}\) = 14.37 cm

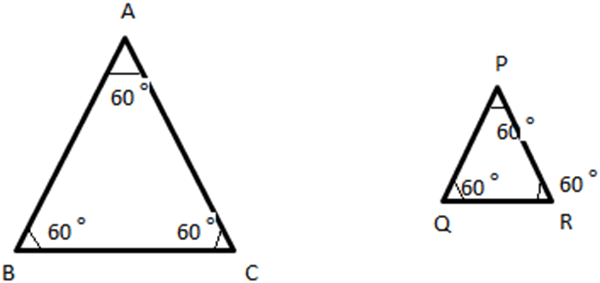
8. If ∠A = ∠P, ∠B = ∠Q, ∠C = ∠R then, ∆ABC & ∆PQR are similar according to which test?
a) AAA test
b) AA test
c) SAS test
d) SSS test
View Answer

Answer: a
Explanation: Since, the angles between the two triangles are equal; therefore the two triangles are similar according to the Angle – Angle – Angle test of similarity.

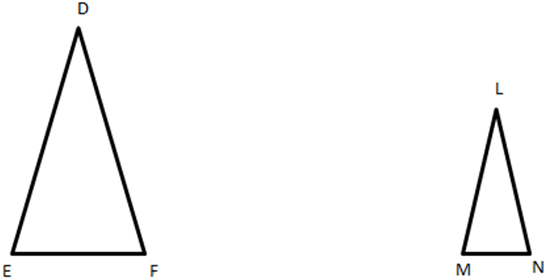
9. If ∠D = ∠L, ∠E = ∠M then, ∆DEF & ∆LMN are similar according to which test?
a) AAA test
b) AA test
c) SAS test
d) SSS test
View Answer

Answer: b
Explanation: Since, the two angles of the triangles are equal; therefore the triangles are similar according to the Angle – Angle test of similarity.

10. If \(\frac {AB}{XY} = \frac {BC}{YZ} = \frac {AC}{XZ}\) then, ∆ABC & ∆XYZ are similar according to which test?
a) AAA test
b) AA test
c) SAS test
d) SSS test
View Answer

Answer: d
Explanation: Since, the sides of the triangle are proportional to each other; therefore the triangles are similar according to the Side – Side – Side test of similarity.

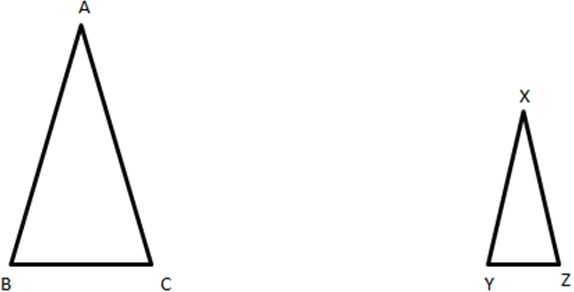
Here, the sides of the triangle are in proportional to each other. Hence, they are similar according to the SSS test.

Sanfoundry Global Education & Learning Series – Mathematics – Class 10.

To practice all chapters and topics of class 10 Mathematics, here is complete set of 1000+ Multiple Choice Questions and Answers.

If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]

« Prev - Class 10 Maths MCQ – Triangles – Similar Figures

» Next - Class 10 Maths MCQ – Triangles

Related Posts:

Recommended Articles: